
第十章 基于秩次的非参数检验 参数:描述总体的指标称为参数。 参数统计:许多统计推断方法,要求来自总 体分布型是已知的,在这种假设基础上,对 总体进行统计推断(进行估计和检验 )称为 参数统计。 非参数检验:不依赖于总体分布类型,也不 对总体参数进行统计推断的假设检验的方法 称为非参数检验:
第十章 基于秩次的非参数检验 参数:描述总体的指标称为参数。 参数统计:许多统计推断方法,要求来自总 体分布型是已知的,在这种假设基础上,对 总体进行统计推断(进行估计和检验)称为 参数统计。 非参数检验:不依赖于总体分布类型,也不 对总体参数进行统计推断的假设检验的方法 称为非参数检验

参数统计内容: 参数估计:1.正态分布的均数和方差(和σ) 2.二项分布的总体率π 3.泊松分布的均数入 与参数有关的检验:1.t检验 2.F检验 3.相关系数检验 4.回归系数检验
参数统计内容: 参数估计: 1.正态分布的均数和方差(μ和σ) 2.二项分布的总体率π 3.泊松分布的均数λ 与参数有关的检验:1.t检验 2.F检验 3.相关系数检验 4.回归系数检验 1

非参检验的优缺点 优点:1、计算简单便于掌握。 2、应用范围广 3、收集资料方便。 缺点:1、损失信息。 2、检验效率低
非参检验的优缺点: 优点:1、计算简单便于掌握。 2、应用范围广。 3、收集资料方便。 缺点:1、损失信息。 2、检验效率低

非参数适用哪些资料: 1、分布型未知 2、能以严重程度、优劣等级、效果大小和 名次先后等等级资料。 3、分布极度偏态。 4、本组内个别变量值偏离过大,远离本组 其它变量值。 5、方差不齐时。 6、筛选或只需获得初步结果
非参数适用哪些资料: 1、分布型未知 2、能以严重程度、优劣等级、效果大小和 名次先后等等级资料。 3、分布极度偏态。 4、本组内个别变量值偏离过大,远离本组 其它变量值。 5、方差不齐时。 6、筛选或只需获得初步结果

第一节配对设计和单样本资料的符号 秩和检验(Vilcoxon配对法) 一、配对设计资料的符号秩和检验 例10-1某研究欲研究保健食品对小鼠抗疲 劳作用,将同种属的小鼠按性别和年龄相 同、体重相近配成对子,共10对,并将每 对中的两只小鼠随机分到保健食品两个不 同的剂量组,过一定时期将小鼠杀死,测 得其肝中糖原含量(mg/100g),结果见表 10-1,问不同剂量组的小鼠肝糖原含量 有无差别?
第一节 配对设计和单样本资料的符号 秩和检验(Wilcoxon配对法) 一、配对设计资料的符号秩和检验 例10-1 某研究欲研究保健食品对小鼠抗疲 劳作用,将同种属的小鼠按性别和年龄相 同、体重相近配成对子,共10对,并将每 对中的两只小鼠随机分到保健食品两个不 同的剂量组,过一定时期将小鼠杀死,测 得其肝中糖原含量(mg/100g),结果见表 10-1,问不同剂量组的小鼠肝糖 原含量 有无差别?
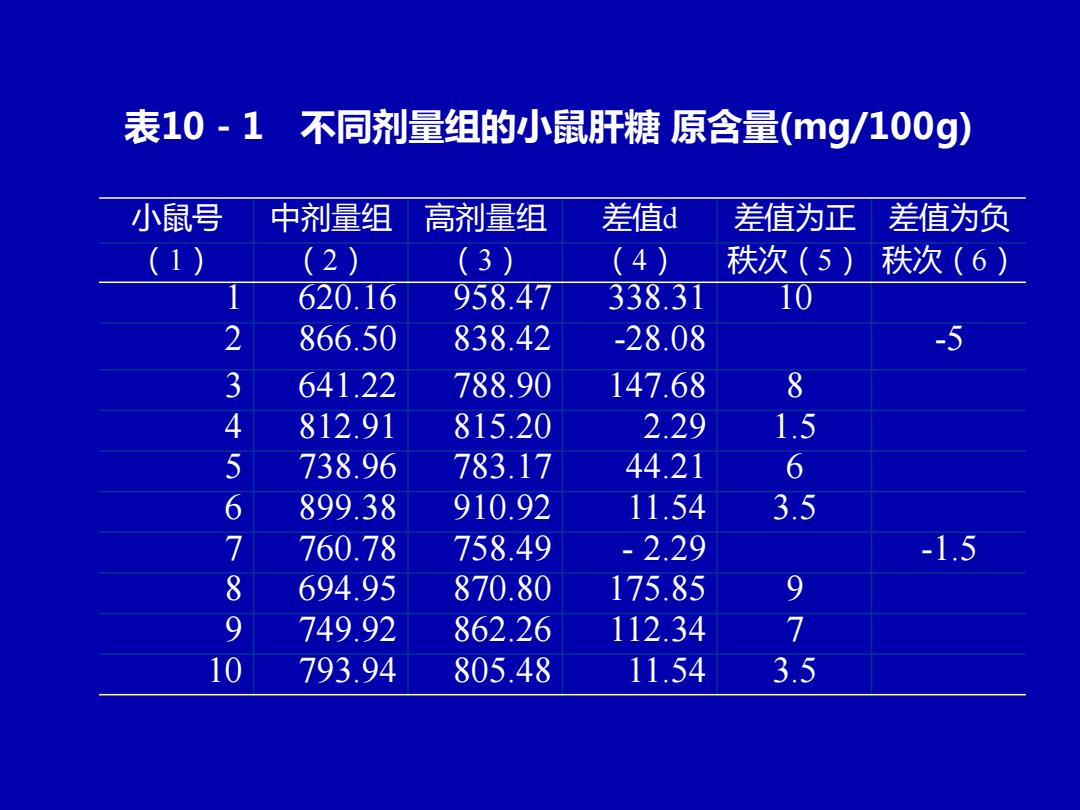
表10-1不同剂量组的小鼠肝糖原含量(mg/100g) 小鼠号 中剂量组 高剂量组 差值d 差值为正 差值为负 (1) (2) (3) (4) 秩次(5) 秩次(6) 620.16 958.47 338.31 10 2 866.50 838.42 -28.08 3 641.22 788.90 147.68 8 4 812.91 815.20 2.29 1.5 5 738.96 783.17 44.21 6 6 899.38 910.92 11.54 3.5 7 760.78 758.49 -2.29 -1.5 8 694.95 870.80 175.85 9 9 749.92 862.26 112.34 7 10 793.94 805.48 11.54 3.5
表10-1 不同剂量组的小鼠肝糖 原含量(mg/100g) 小鼠号 中剂量组 高剂量组 差值d 差值为正 差值为负 (1) (2) (3) (4) 秩次(5) 秩次(6) 1 620.16 958.47 338.31 10 2 866.50 838.42 -28.08 -5 3 641.22 788.90 147.68 8 4 812.91 815.20 2.29 1.5 5 738.96 783.17 44.21 6 6 899.38 910.92 11.54 3.5 7 760.78 758.49 - 2.29 -1.5 8 694.95 870.80 175.85 9 9 749.92 862.26 112.34 7 10 793.94 805.48 11.54 3.5

1、检验步骤: (1)假设:H0:差值总体中位数M。=0 H:Ma 0 (2)求差值: (3)编秩 (4)求秩和并确定检验统计量:分别求正负秩次 之和,正秩次的和以T表示,负秩次的和以T表示 本例T+为48.5,T为6.5,以绝对值较小秩和作检 验统计量,本例取T=6.5.当小于等于50时,查T 界值表.注意: 当<5时,应用秩和检验不能得出双侧有统计 学意义的概率故n必须大于或等于5
1、检验步骤: (1)假设:H0:差值总体中位数Md=0 H1 : Md 0 (2)求差值: (3)编秩: (4)求秩和并确定检验统计量:分别求正负秩次 之和,正秩次的和以T+表示,负秩次的和以T-表示. 本例T+为48.5,T-为6.5,以绝对值较小秩和作检 验统计量,本例取T=6.5.当n小于等于50时,查T 界值表.注意: • 当n<5时,应用秩和检验不能得出双侧有统计 学意义的概率故n必须大于或等于5

3、正态近似法 ·若n>50超过附表9的范围,可用Z检验。 T-n(n+1)/4-0.5 Z n(n+1)(2n+1) ∑-1,) 24 48
3、正态近似法: • 若n>50超过附表9的范围,可用Z 检验

式中t:第个相同差值的个数 假定差值中有2个4,5个6,3 个7则t1=2,t2=5,t3=3, ∑k-,=2-2+5-5+3-3=150
式中tj:第j个相同差值的个数, 假定差值中有2个4,5 个6,3 个7则t1=2, t2=5,t3=3

本法基本思想 假定从一总体中随机抽取=5的样本,按例题 9.1的方法和步骤,可求出TT.,当重复抽取所有 可能组合情况如T=5可有三种情况,一是最大的差 值为正,其余4个为负,故正秩和等于5;二是差值的绝 对值排在第一位及第四位,其余为负,即T=1+4;二 是差值的绝对值排在第三位和第二位,其余为负,即 T=2+3。 由此可看出T分布为以均数为中心对称的非连续分 布。随着n值的增大,T的分布逐渐接近均数为 n(n+1)/4,方差为n(n+1)(2n+1)/24的正态分布 (>25),即然为正态分就可按正态分布的原理进 行T的推断
本法基本思想: 假定从一总体中随机抽取n=5 的样本,按例题 9.1的方法和步骤,可求出T+、 T-,当重复抽取所有 可能组合情况.如T=5可有三种情况,一是最大的差 值为正,其余4个为负,故正秩和等于5;二是差值的绝 对值排在第一位及第四位,其余为负,即T=1+4;二 是差值的绝对值排在第三位和第二位,其余为负,即 T=2+3。 由此可看出T分布为以均数为中心对称的非连续分 布。随着n值的增大,T的分布逐渐接近均数为 n(n+1)/4,方差为n(n+1)(2n+1)/24的正态分布 (n>25),即然为正态分就可按正态分布的原理进 行T的推断