
第十章基于秩次的非参数检验 姿徽医科大学流行病与卫生统计学系 潘发明 famingpan@ahmu.edu.cn
第十章 基于秩次的非参数检验 安徽医科大学流行病与卫生统计学系 潘发明 famingpan@ahmu.edu.cn

◆ 参数统计(parametric statistics):以样本来自已 知分布(如正态分布)总体为假设基础,对未知 总体参数进行估计或检验的方法,如t检验、Z 检验和方差分析等; ◆非参数统计(nonparametric statistics):总体分布 不易确定,或分布呈明显偏态、方差不齐又无适 当的变量转换方法以满足参数统计条件。 非参数统计比较分布而不是比较参数。 2
2 参数统计(parametric statistics):以样本来自已 知分布(如正态分布)总体为假设基础,对未知 总体参数进行估计或检验的方法,如t 检验、Z 检验和方差分析等; 非参数统计(nonparametric statistics):总体分布 不易确定,或分布呈明显偏态、方差不齐又无适 当的变量转换方法以满足参数统计条件。 非参数统计比较分布而不是比较参数

非参数统计的优点与缺点 优点: ①适用范围广,不受总体分布的限制(但是不是等同于任何分 布)氵 ②对数据的要求不严,如某些指标难以准确测定,只 能以严重程度、优劣等级、先后次序等表示的资料 也可应用; ③方法简便,易于理解和掌握; ④具有较好的稳健性。 缺点: 如果对符合参数检验的资料应用非参数检验,因不能充分利用 资料提供的信息,会使检验效能低于参数检验;若要使检验效 能相同往往需要更大的样本含量。 3
3 非参数统计的优点与缺点 优点: ①适用范围广,不受总体分布的限制(但是不是等同于任何分 布); ②对数据的要求不严,如某些指标难以准确测定,只 能以严重程度、优劣等级、先后次序等表示的资料 也可应用; ③方法简便,易于理解和掌握; ④具有较好的稳健性。 缺点: 如果对符合参数检验的资料应用非参数检验,因不能充分利用 资料提供的信息,会使检验效能低于参数检验;若要使检验效 能相同往往需要更大的样本含量

秩次、秩和及相持的概念 秩次(rank),秩统计量 是指全部观察值按某种顺序排列的位序 秩和(rank sum) 同组秩次之和 相持(tie) 某两个或某几个数值相同,应该编制相同的秩次,但在不同组之间应 该取平均秩次。相持是指具有相同秩次的个数。 4
4 秩次、秩和及相持的概念 • 秩次(rank),秩统计量 是指全部观察值按某种顺序排列的位序 • 秩和(rank sum) 同组秩次之和 • 相持(tie) 某两个或某几个数值相同,应该编制相同的秩次,但在不同组之间应 该取平均秩次。相持是指具有相同秩次的个数

非参数检验的应用领域 1、分布型未知 2、能以严重程度、优劣等级、效果大小和名 次先后等等级资料。 3、分布极度偏态。 4、本组内个别变量值偏离过大,远离本组其它变量值。 5、方差不齐时。 6、筛选或只需获得初步结果。 5
5 非参数检验的应用领域 1、分布型未知 2、能以严重程度、优劣等级、效果大小和名 次先后等等级资料。 3、分布极度偏态。 4、本组内个别变量值偏离过大,远离本组其它变量值。 5、方差不齐时。 6、筛选或只需获得初步结果

主要内容 配对设计的符号秩和检验 成组设计两样本比较的秩和检验 成组设计多样本比较的秩和检验 随机区组设计资料的秩和检验 6
6 主要内容 • 配对设计的符号秩和检验 • 成组设计两样本比较的秩和检验 • 成组设计多样本比较的秩和检验 • 随机区组设计资料的秩和检验

第一节配对设计的符号秩和检验 Wilcoxon符号秩和检验(Wilcoxon signed rank test) 是推断其差值是否来自中位数为零的总体的方法 可用于: 配对设计的两样本的比较 ·单一样本与总体中位数的比较 7
7 第一节 配对设计的符号秩和检验 Wilcoxon符号秩和检验(Wilcoxon signed rank test) 是推断其差值是否来自中位数为零的总体的方法, 可用于: ▪ 配对设计的两样本的比较 ▪ 单一样本与总体中位数的比较
→、 配对设计的两样本的比较 例10.1某医院用中草药 “抗苯一号”治疗9例苯中毒 患者,其治疗前后的白细胞总数如表10-1,问该药是 否对患者的白细胞总数有影响? 表10-19名苯中毒患者治疗前后白细胞总数结果(单位为10L) 病人号 治疗前 治疗后 差值d 秩次 (1) (2) (3) (4) (2) -(3) (5) 6.0 4.2 1.8 6.5 4.8 5.5 -0.7 -4.5 2345678 4.5 6.3 -1.8 -6.5 3.4 3.8 -0.4 3 7.0 4.4 2.6 3.8 4.0 -0.2 -2 5.9 0.1 8.0 -4.5 -9 9 43 5.0 -0.7 -4.5 T=15.5 T=29.5 8
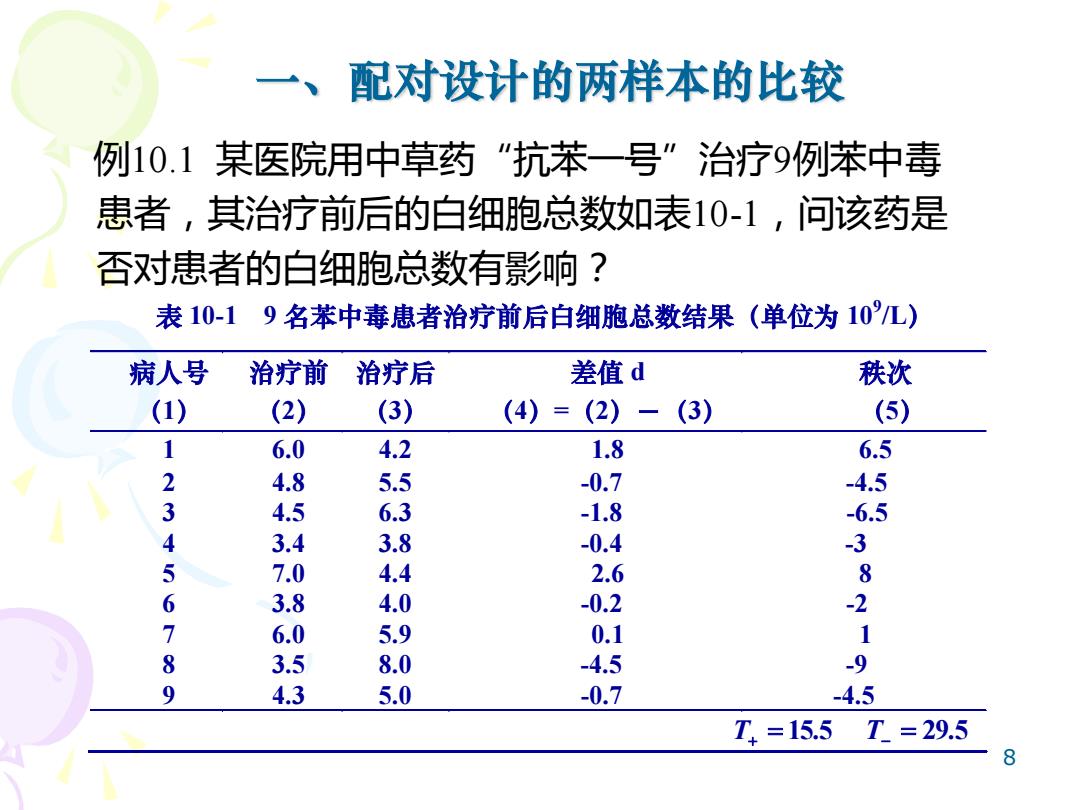
8 一、配对设计的两样本的比较 例10.1 某医院用中草药“抗苯一号”治疗9例苯中毒 患者,其治疗前后的白细胞总数如表10-1,问该药是 否对患者的白细胞总数有影响? 表 10-1 9 名苯中毒患者治疗前后白细胞总数结果(单位为 109 /L) 病人号 (1) 治疗前 (2) 治疗后 (3) 差值 d (4)=(2)-(3) 秩次 (5) 1 6.0 4.2 1.8 6.5 2 4.8 5.5 -0.7 -4.5 3 4.5 6.3 -1.8 -6.5 4 3.4 3.8 -0.4 -3 5 7.0 4.4 2.6 8 6 3.8 4.0 -0.2 -2 7 6.0 5.9 0.1 1 8 3.5 8.0 -4.5 -9 9 4.3 5.0 -0.7 -4.5 = 15.5 T+ T− = 29.5

配对设计两样本比较 查表法(n≤50) 1.建立检验假设,确定检验水准 Ho:Ma-0 H:Mat0 0=0.05 2.计算检验统计量T值 ()求各对的差值 (2) 编秩按差值的绝对值由小到大编秩,依差值的正负 给秩次冠以正负号。编秩时,若差值为0,舍去不计; 若差值的绝对值相等,则取其平均秩次。 9
9 查表法(n≤50) 1.建立检验假设,确定检验水准 H0 : Md =0 H1 : Md≠0 α= 0.05 2.计算检验统计量T值 (1) 求各对的差值 (2) 编秩 按差值的绝对值由小到大编秩,依差值的正负 给秩次冠以正负号。编秩时,若差值为0,舍去不计; 若差值的绝对值相等,则取其平均秩次。 配对设计两样本比较

配对设计两样本比较 3)求秩和并确定统计量T 分别求出正、负秩次之和, 正秩和以T表示,负秩和以T表示,可任取正秩和或 负秩和为统计量工。 T+T.=n(n+1)/2,n为不等于0的对子数。 3.确定P值,做出推断结论 当≤50时,以T值查附表9T界值表(配对设计用), 若检验统计量T值在T界值范围内,则P值大于相应的 概率水平;若T值在T界值范围外或等于界值,则P值 小于或等于相应的概率水平。 10
10 (3) 求秩和并确定统计量T 分别求出正、负秩次之和, 正秩和以T+表示,负秩和以T-表示,可任取正秩和或 负秩和为统计量T。 T++T-=n(n+1)/2,n为不等于0的对子数。 3.确定P值,做出推断结论 当n≤50时,以T值查附表9 T界值表(配对设计用), 若检验统计量T值在T界值范围内,则P值大于相应的 概率水平;若T值在T界值范围外或等于界值,则P值 小于或等于相应的概率水平。 配对设计两样本比较