
例 某克山病区测定10例克山病患者与10名健康人的血磷 值(mmo/L)如下,问该地克山病患者与健康人的血磷 值是否不同? 患者:0.841.640.750.760.811.161.201.341.351.48 健康人:0.540.051.201.201.391.531.671.801.872.07 变异的分解 1. 总变异:全部实验数据大小不等 2ΣK,-)=(W-) V总=N一1 2. 组间变异:各处理组的样本均数 也大小不等 SS组间 ∑n,(区,-x月 V组间k一1 MS▣=SS组间/V组间(反映了处理因素的作用,同时也包括了随 机误差)
例 某克山病区测定10例克山病患者与10名健康人的血磷 值(mmol/L ) 如下,问该地克山病患者与健康人的血磷 值是否不同? 患者:0.84 1. 64 0.75 0.76 0.81 1.16 1.20 1.34 1.35 1.48 健康人: 0.54 0. 05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 变异的分解: 1. 总变异: 全部实验数据大小不等 ν总=N-1 2. 组间变异:各处理组的样本均数 也大小不等 ν组间=k-1 MS组间=SS组间/ ν组间 (反映了处理因素的作用,同时也包括了随 机误差)

3.组内变异 各处理组内部的观察值也大小不等。它反 映了观察值的随机误差(包括个体差异以及测定误差) SS组内=】 2(k,-)=∑a-1 V组内=N一k MS组内-=SS组内/V组内 SS总=SS组内十SS组间,且V总=V组间tV组内。 F=MS组间/MS组内 Fa F之Fu Pc
3. 组内变异 各处理组内部的观察值也大小不等。它反 映了观察值的随机误差(包括个体差异以及测定误差) MS组内=SS组内/ ν组内 ν组内=N-k SS总=SS组内+SS组间,且ν总=ν组间+ν组内。 F=MS组间/MS组内 ( ) ,P 组间, 组内 F F ( ) ,P 组间, 组内 F F

方差分析的基本思想:根据资料的设计类型及研究 目的,即按变异的不同来源将全部观察值间的总变异分 为两部分或多个部分,其自由度也分解为相应的部分 除随机误差外,其余每个部分的变异可由某个因素的作 用加以解释,(如各组均数间的变异SS组间可由处理因素 的作用加以解释),通过比较可能由某因素所致变异的 均方与随机误差的均方,借助F分布作出统计推断,从 而了解该因素对观测指标有无影响。 方差分析的应用条件是:1)各样本是相互独立的随机 样本;即任何两个观察值之间均不相关;2)各样本来 自正态总体;3)各处理组总体方差相等,即方差齐 (homogeneity of variance)。简单地概括为任何观 察值X都是独立地来自具有等方差的正态总体
方差分析的基本思想:根据资料的设计类型及研究 目的,即按变异的不同来源将全部观察值间的总变异分 为两部分或多个部分,其自由度也分解为相应的部分, 除随机误差外,其余每个部分的变异可由某个因素的作 用加以解释,(如各组均数间的变异SS组间可由处理因素 的作用加以解释),通过比较可能由某因素所致变异的 均方与随机误差的均方,借助F分布作出统计推断,从 而了解该因素对观测指标有无影响。 方差分析的应用条件是:1)各样本是相互独立的随机 样本;即任何两个观察值之间均不相关;2)各样本来 自正态总体;3)各处理组总体方差相等,即方差齐 (homogeneity of variance)。简单地概括为任何观 察值Xij都是独立地来自具有等方差的正态总体

二、 完全随机设计资料方差分析的基本步骤 完全随机设计资料的方差分析用于成组设 计的多个样本均数的比较可用单因素 方差分析。该分析中仅涉及一个研究 因素,此因素有K(K≥2)个水平或状 态 无论是实验还是观察,研究目的都是比 较不同水平下,各组平均值之间的差别是否 具有统计学意义,这种多个样本均数的比较 都可用单因素方差分析
二、完全随机设计资料方差分析的基本步骤 完全随机设计资料的方差分析用于成组设 计的多个样本均数的比较可用单因素 方差分析。该分析中仅涉及一个研究 因素,此因素有K(K≥2)个水平或状 态。 无论是实验还是观察,研究目的都是比 较不同水平下,各组平均值之间的差别是否 具有统计学意义,这种多个样本均数的比较 都可用单因素方差分析

1.成组设计方差分析中变异的分解 总变异 组内变异:个体差异及血糖 (三个组共60人 的随机测定误差。 的餐后2小时血糖 测定值大小不等 该变异既包含随 机误差,又包含 组间变异:不同用药的影响 了三组用药即处 及随机测量误差 理的不同)
1. 成组设计方差分析中变异的分解 总变异 (三个组共60人 的餐后2小时血糖 测定值大小不等; 该变异既包含随 机误差,又包含 了三组用药即处 理的不同) 组内变异: 个体差异及血糖 的随机测定误差。 组间变异: 不同用药的影响 及随机测量误差
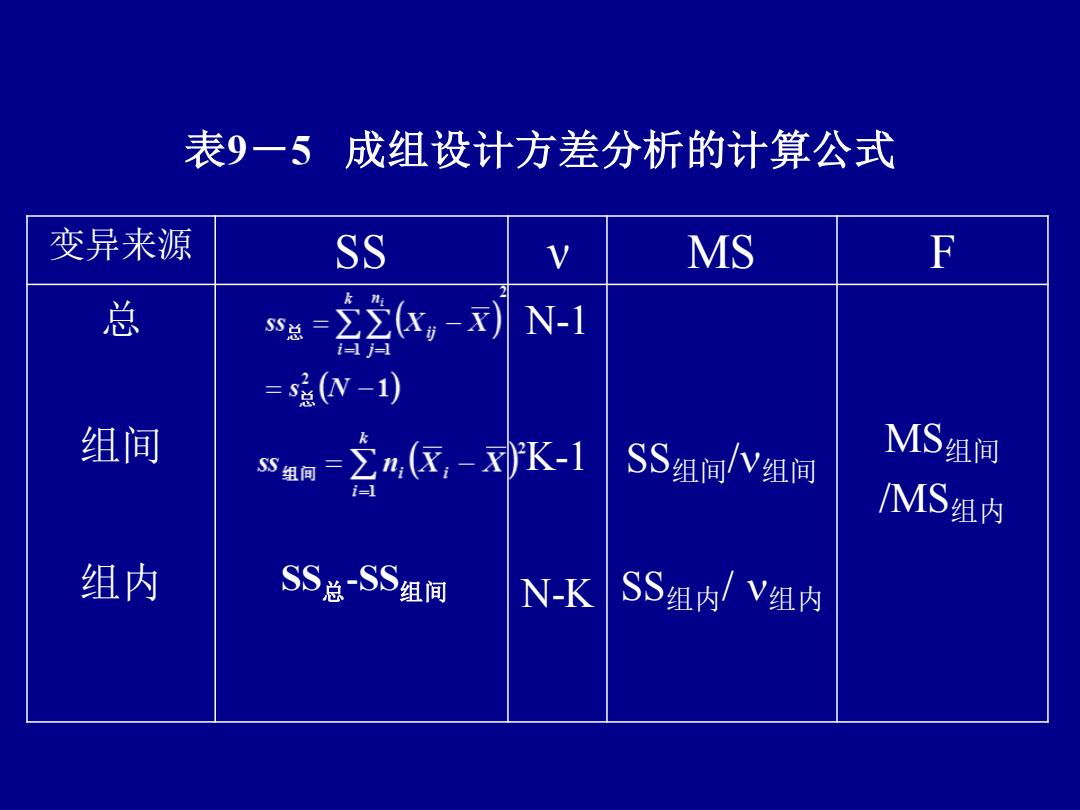
表9一5成组设计方差分析的计算公式 变异来源 SS V MS F 总 “2化,-列 N-1 =短(N-1) 组间 ∑n,(仅,-xK-1SS组同y组间 MS组间 MS组内 组内 SS总-SS组间 N-K SS组内V组内
表9-5 成组设计方差分析的计算公式 变异来源 SS ν MS F 总 组间 组内 N-1 K-1 N-K SS组间/组间 SS组内/ 组内 MS组间 /MS组内 SS总-SS组间

2、分析计算步骤 (1)建立假设并确定检验水准 Ho:三个总体均数相等 即μ1=μ2=3 H1:三个总体均数不等或不全相等 c=0.05 (2) 计算检验统计量F值
2、分析计算步骤 (1) 建立假设并确定检验水准 H0: 三个总体均数相等, 即μ1= μ2= μ3 H1: 三个总体均数不等或不全相等 α=0.05 (2) 计算检验统计量F值

SSa=S2(N-118.4176(60-1)=1086.6384 SS组向=∑n,(民,-}=219.1952-6.8650月 +195.8000-6.8650+20(5.4300-6.8650) =176.7621 V组间一3-1=2 MS SS间 176.7621 组间 =88.3806 V组间 2 SS组内=SS急一SS组间-1086.6384-176.7621=909.8723Y组内=59-2=57 MS组内 SS组内 909.8723 =15.9627 V组内 57 MS. 组间 88.3806 F= =5.537 MS组内 15.9627
( ) ( ) ( ) ( ) ( ) ( ) = = = = = = = - = - = = - = = = = = = -= + - + - = - = - = 组内 组间 组内 组内 组内 组内 总 组间 组内 组间 组间 组间 组间 组间 总 总 5.537 15.9627 88.3806 MS MS F 15.9627 57 SS 909.8723 MS SS SS SS 1086.6384 176.7621 909.8723 59 2 57 88.3806 2 SS 176.7621 MS 176.7621 3 1 2 19 5.8000 6.8650 20 5.4300 6.8650 SS 21 9.1952 6.8650 SS S N 1 18.4176 60 1 1086.6384 2 2 2 2 2 − = − = n x x i i i

3).确定P值并作出推断结论 以分子的自由度V组▣=2为1,分母的自由 度V组内=57 为V2,查附表3.1,方差分析用F界值表 F0.052,60)=3.15F0.012,60=4.98,F=5.537 >F0.012,60=4.98 P<0.01。 在@=0.05水准上拒绝H0,接受H可以认 为三种人的血糖水平不同
3). 确定P值并作出推断结论 以分子的自由度ν组间 =2为ν1,分母的自由 度ν组内 =57 为ν2,查附表3.1,方差分析用F界值表 , F0.05(2,60)=3.15 F0.01(2,60)=4.98,F=5.537 > F0.01(2,60)=4.98, P <0.01。 在α=0.05水准上拒绝H0,接受 H1可以认 为三种人的血糖水平不同

表9一6例9一1的方差分析表 变异来源 SS df MS F P 组间(处理组间) 176.7612 288.3806 5.537 <0.01 组内(误差) 909.8723 5715.9627 总 1086.6335 59
表9-6 例9-1的方差分析表 变异来源 SS df MS F P 组间(处理组间) 176.7612 2 88.3806 5.537 <0.01 组内(误差) 909.8723 57 15.9627 总 1086.6335 59