
方差分折 讲授内容 方差分析的基本思想及应用条件 完全随机设计资料的方差分析 随机区组设计资料的方差分析 多个样本均数间的多重比较
方差分析 讲授内容 方差分析的基本思想及应用条件 完全随机设计资料的方差分析 随机区组设计资料的方差分析 多个样本均数间的多重比较

研究因素为k个 当k=2时,两组总体均数处比较是否相等可采 用前面介绍的检验(当然也可采用今天所介 绍的方差分析 当k>2时,即检验两组以上的总体均数是否相 等时,检验已不能满足要求,需采用方差分 (analysis of variance ANOVA)
研究因素为k个: 当k=2时,两组总体均数比较是否相等可采 用前面介绍的t检验(当然也可采用今天所介 绍的方差分析) 当k>2时,即检验两组以上的总体均数是否相 等时,t检验已不能满足要求,需采用方差分 析(analysis of variance ,ANOVA)

例9-1某医生为研究一种四类降糖新药的疗效 1 以统一的纳入标准和排除标准选择了60名2型糖尿 病患者,按完全随机设计方案将患者分为三组进行 双盲临床试验。其中,降糖新药高剂量组21人,低 剂量组19人,对照20人。对照组服用公认的降糖药 物,治疗4周后测得其餐后2小时血糖的下降值 ( mmol/L),结果如表9-1所示。问治疗4周后,餐 后2小时血糖下降值的总体平均水平是否不同?
例9-1 某医生为研究一种四类降糖新药的疗效, 以统一的纳入标准和排除标准选择了60名2型糖尿 病患者,按完全随机设计方案将患者分为三组进行 双盲临床试验。其中,降糖新药高剂量组21人,低 剂量组19人,对照20人。对照组服用公认的降糖药 物,治疗4周后测得其餐后2小时血糖的下降值 (mmol/L),结果如表9-1所示。问治疗4周后,餐 后2小时血糖下降值的总体平均水平是否不同?
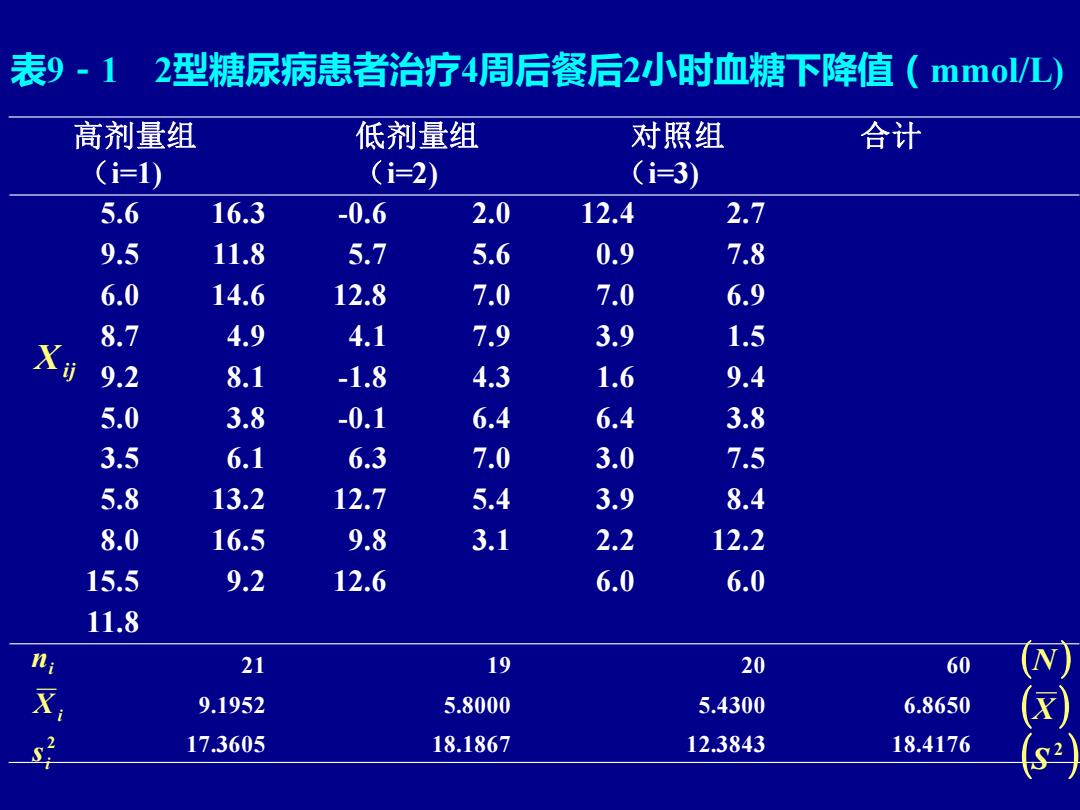
表9-12型糖尿病患者治疗4周后餐后2小时血糖下降值(mmol/L) 高剂量组 低剂量组 对照组 合计 (=1) (i=2) (i-3) 5.6 16.3 -0.6 2.0 12.4 2.7 9.5 11.8 5.7 5.6 0.9 7.8 6.0 14.6 12.8 7.0 7.0 6.9 X 8.7 4.9 4.1 7.9 3.9 1.5 9.2 8.1 -1.8 4.3 1.6 9.4 5.0 3.8 -0.1 6.4 6.4 3.8 3.5 6.1 6.3 7.0 3.0 7.5 5.8 13.2 12.7 5.4 3.9 8.4 8.0 16.5 9.8 3.1 2.2 12.2 15.5 9.2 12.6 6.0 6.0 11.8 ni 21 19 20 60 9.1952 5.8000 5.4300 6.8650 17.3605 18.1867 12.3843 18.4176 s
表9-1 2型糖尿病患者治疗4周后餐后2小时血糖下降值(mmol/L) 高剂量组 (i=1) 低剂量组 (i=2) 对照组 (i=3) 合计 5.6 16.3 -0.6 2.0 12.4 2.7 9.5 11.8 5.7 5.6 0.9 7.8 6.0 14.6 12.8 7.0 7.0 6.9 8.7 4.9 4.1 7.9 3.9 1.5 9.2 8.1 -1.8 4.3 1.6 9.4 5.0 3.8 -0.1 6.4 6.4 3.8 3.5 6.1 6.3 7.0 3.0 7.5 5.8 13.2 12.7 5.4 3.9 8.4 8.0 16.5 9.8 3.1 2.2 12.2 15.5 9.2 12.6 6.0 6.0 11.8 21 19 20 60 9.1952 5.8000 5.4300 6.8650 17.3605 18.1867 12.3843 18.4176 Xij 2 i i i s X n ( ) ( ) ( ) 2 S X N

上述资料如采用前面所学两样本检验进行 两两比较,而得出结论,会使犯第一类错误的 概率增大
上述资料如采用 前面所学两样本t检验进行 两两比较,而得出结论,会使犯第一类错误的 概率增大

高剂譴塑 低剂量盟 对盟 针 (包 基本思想及应用条件 561636 20124 21 95 18 560918 总变异 60 1 月0 10 128 10 69 87 39 15 92 0 0.1 18 43 16 94 50 381 6464 38 35 61 63 1.0 30 15 5.8 132 127 54 3984 处理+随机误差 随机误差 80 16598 3122122 155 92 12.6 60 6.0 18 21 19 20 60 9192 580 5430 68650 17365 181867 12383 18476
基本思想及应用条件 总变异 处理+随机误差 随机误差 17.3605 18.1867 12.3843 18.4176 9.1952 5.8000 5.4300 6.8650 21 19 20 60 11.8 15.5 9.2 12.6 6.0 6.0 8.0 16.5 9.8 3.1 2.2 12.2 5.8 13.2 12.7 5.4 3.9 8.4 3.5 6.1 6.3 7.0 3.0 7.5 5.0 3.8 -0.1 6.4 6.4 3.8 9.2 8.1 -1.8 4.3 1.6 9.4 8.7 4.9 4.1 7.9 3.9 1.5 6.0 14.6 12.8 7.0 7.0 6.9 9.5 11.8 5.7 5.6 0.9 7.8 5.6 16.3 -0.6 2.0 12.4 2.7 对照组 合计 (i=3) 低剂量组 (i=2) 高剂量组 (i=1) 17.3605 18.1867 12.3843 18.4176 9.1952 5.8000 5.4300 6.8650 21 19 20 60 11.8 15.5 9.2 12.6 6.0 6.0 8.0 16.5 9.8 3.1 2.2 12.2 5.8 13.2 12.7 5.4 3.9 8.4 3.5 6.1 6.3 7.0 3.0 7.5 5.0 3.8 -0.1 6.4 6.4 3.8 9.2 8.1 -1.8 4.3 1.6 9.4 8.7 4.9 4.1 7.9 3.9 1.5 6.0 14.6 12.8 7.0 7.0 6.9 9.5 11.8 5.7 5.6 0.9 7.8 5.6 16.3 -0.6 2.0 12.4 2.7 对照组 合计 (i=3) 低剂量组 (i=2) 高剂量组 (i=1)

基本思想及应用条件 基本思想: 根据资料设计的类型及 研究目的,将总变异分解为两个或 多个部分,每个部分的变异可由某 因素的作用来解释。通过上比较可能 由某因素所至的变异与随机误差 即可了解该因素对测定结果有无影 响
基本思想及应用条件 • 基本思想:根据资料设计的类型及 研究目的,将总变异分解为两个或 多个部分,每个部分的变异可由某 因素的作用来解释。通过比较可能 由某因素所至的变异与随机误差, 即可了解该因素对测定结果有无影 响

基本思想及应用条件 应用条件 1)各样本是相互独立的随机样本 2)各样本来自正态总体 3)各处理组总体方差相等, 即方差 齐
• 应用条件: 1)各样本是相互独立的随机样本 2)各样本来自正态总体 3)各处理组总体方差相等,即方差 齐 基本思想及应用条件

第一节完全随机设计资料的方差分析
第一节 完全随机设计资料的方差分析

一、 方差分析的基本思想 表9-4方差分析试验数据示意图 用X表示第个处理组的第 第1组 第2组… 第k组 个观察值,或简记为X,总 Xu X21 Xi X12 X22 Xk2 例数N=∑n。第i个处理组 的均数用表示,全部实验 X2n2 结果的总均数用表示丞。 X2 X X n n2 nk N 方差分析的目的就是通过分析各个处理组均数 之间的差别,推断它所代表的k个总体均数间是否存 在差别,或水个处理组间均数的差别是否具有统计学意 义
一、方差分析的基本思想 用Xij表示第i个处理组的第j 个观察值,或简记为X,总 例数N =∑ni。第i个处理组 的均数用 表示,全部实验 结果的总均数用 表示。 方差分析的目的就是通过分析各个处理组均数 之间的差别,推断它所代表的k个总体均数间是否存 在差别,或k个处理组间均数的差别是否具有统计学意 义。 表9-4 方差分析试验数据示意图