
第十二章简单回归分析 前面介绍了两变量间关联性分析,本 章与下一章我们将进一步的介绍观察数据 中变量间的数量依存性的回归关系。 第一节{ 简单直线回归
第十二章 简单回归分析 前面介绍了两变量间关联性分析,本 章与下一章我们将进一步的介绍观察数据 中变量间的数量依存性的回归关系。 第一节 简单直线回归

直线回归的概念及其统计描述 在上一章中,对15名健康人疑血浓度 (Y)与凝血时间(X)数据计算相关系数 定量猫述了变量间关联性的强弱程度与方 向。为直观地说明直线▣归的概念,我们 以以上一章中对15名健康人凝血浓度与凝 血时间数据为例,来探讨两变量间依存变 化关系 反应变量(Y)与自变量(X)的简单线性模 simple linear regression model 可表达为 Y=a+BX:+8
一、直线回归的概念及其统计描述 在上一章中,对15名健康人凝血浓度 (Y)与凝血时间(X)数据计算相关系数, 定量描述了变量间关联性的强弱程度与方 向。为直观地说明直线回归的概念,我们 以以上一章中对15名健康人凝血浓度与凝 血时间数据为例,来探讨两变量间依存变 化关系。 反应变量(Y)与自变量(X)的简单线性模 型(simple linear regression model) 可表达为: Yi Xi i = + +

表12·115名健康成人凝血时间与凝血酶浓度测量值 受试者号 12345 6 8 910111213 14 15 X 1.11.21.0 0.91.2 1.10.9 0.61.0 0.9 1.1 09 1.1 1.0 0.7 1413 151513 14161714 161516141517 在通常情况下,研究者只能获取一定数 量的样本数据,用该样本数据建立的有关Y 与X变化的线性方程称为回归方程 (regression equation)嘢x
表12-1 15名健康成人凝血时间与凝血酶浓度测量值 在通常情况下,研究者只能获取一定数 量的样本数据,用该样本数据建立的有关Y 与X变化的线性方程称为回归方程 (regression equation)即: 受试者号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 X 1.1 1.2 1.0 0.9 1.2 1.1 0.9 0.6 1.0 0.9 1.1 0.9 1.1 1.0 0.7 Y 14 13 15 15 13 14 16 17 14 16 15 16 14 15 17 Y ˆ = a +bX

在描述两变量的关系时,一般把两个变量中能 精确容易测量的作自变量,不易测量作为因变量: 即用易测量的数据X估计不易测量的另一数据。如 年龄估算小儿体重等。在描述凝血时间与凝血浓度 的依存关系中,将凝血酶浓度作为自变量(X), 凝血时间作为应变量(Y)。由图12-1可见,凝 血时间随凝血酶浓度增大而减少且呈直线趋势,但 并非15点恰好全部都在一直线上。两变量数量间虽 然存在一定关系,但不是十分确定的。这与两变量 间严格对应的函数关系不同,称为直线回归 (Linear regression)。直线回归是回归分析中 最基本、最简单的一种,故又称简单simple regression)
在描述两变量的关系时,一般把两个变量中能 精确容易测量的作自变量,不易测量作为因变量。 即用易测量的数据X估计不易测量的另一数据。如 年龄估算小儿体重等。在描述凝血时间与凝血浓度 的依存关系中,将凝血酶浓度作为自变量( X ), 凝血时间作为应变量(Y)。由图12-1可见,凝 血时间随凝血酶浓度增大而减少且呈直线趋势,但 并非15点恰好全部都在一直线上。两变量数量间虽 然存在一定关系,但不是十分确定的。这与两变量 间严格对应的函数关系不同,称为直线回归 (Linear regression)。直线回归是回归分析中 最基本、最简单的一种,故又称简单simple regression)
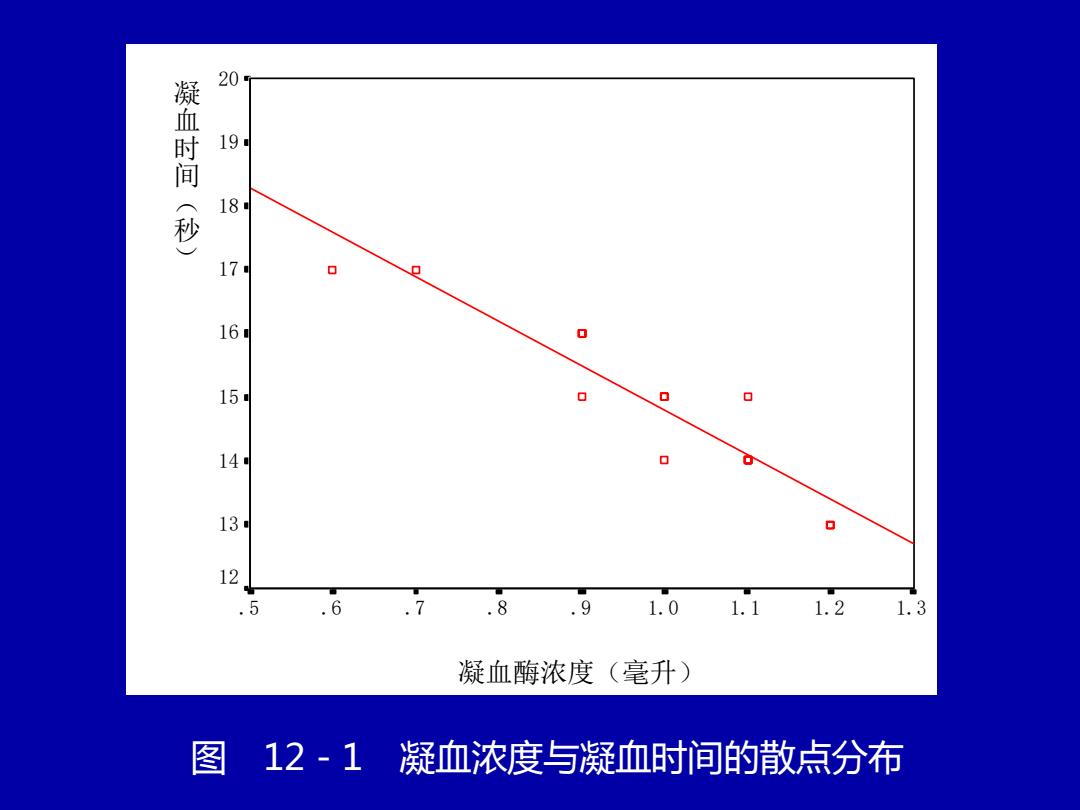
凝血时间(秒) 09 18 17 16 15 14 13 12 .5 .6 .7 .8.9 1.0 1.1 1.2 1.3 凝血酶浓度(毫升) 图 12-1 凝血浓度与凝血时间的散点分布
图 12-1 凝血浓度与凝血时间的散点分布 凝血酶浓度(毫升) .5 .6 .7 .8 .9 1.0 1.1 1.2 1.3 凝 血 时 间 ( 秒 ) 20 19 18 17 16 15 14 13 12

二、回归模型的前提假设 线性回归模型的前提条件是:线性 (linear)、独立(independent),正态 (normal),等方差(equal variance) 1、线性是指反应变量Y的总体平均值与自 变量X呈线性关系。 2、独立是指任意两观察值互相独立 3、正态性假定是指线性模型的误差项ε服 从正态分布, 4、等方差是指在自变量X取值范围内,不 论X取什么值,Y都具有相同的方差:
二、回归模型的前提假设 线性回归模型的前提条件是:线性 (linear)、独立(independent),正态 (normal),等方差(equal variance) 1、线性是指反应变量Y的总体平均值与自 变量X呈线性关系。 2、独立是指任意两观察值互相独立。 3、正态性假定是指线性模型的误差项i服 从正态分布。 4、等方差是指在自变量X取值范围内,不 论X取什么值,Y都具有相同的方差
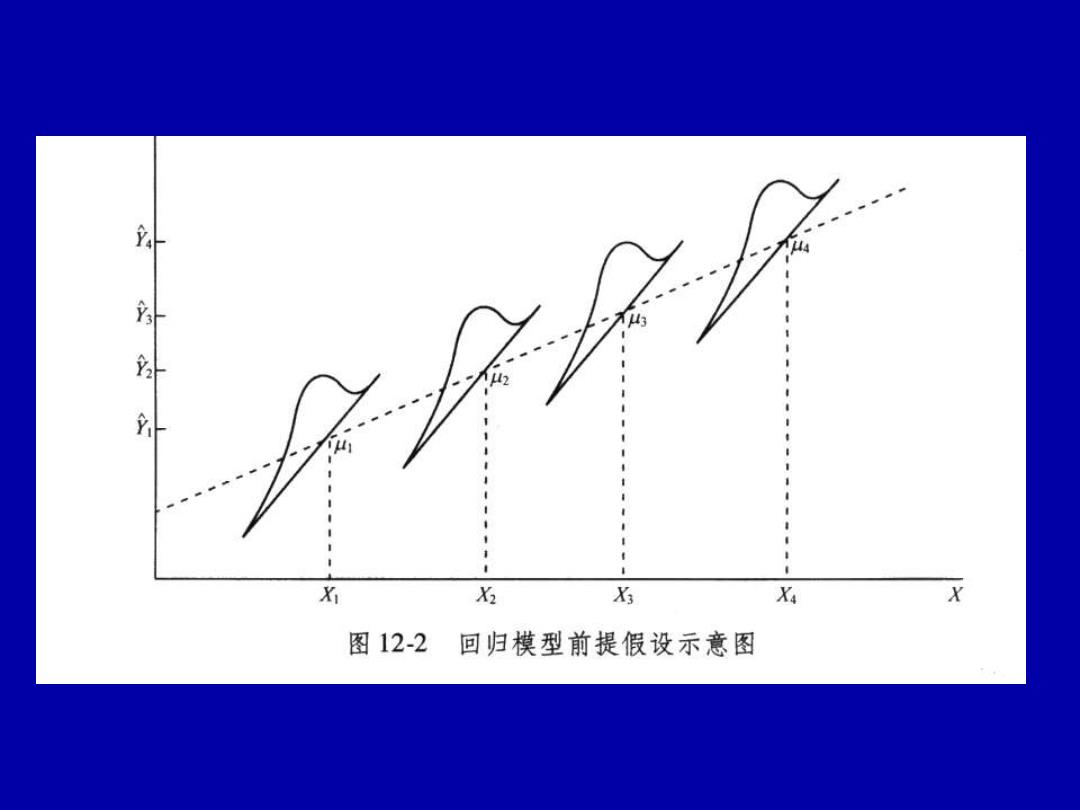
X X2 X Xa X 图12-2 回归模型前提假设示意图

三、回归参数的估计 一)回归参数估计的最小二乘原则 参数α与一般只能通过样本数据来估计。 当X取值为X时,Y的平均值的估计 应为a+bX而实际观察值为Y。两者之差 称为残差(residual),即,=y,-(a+bX,) 当a与b取不同值时获取不同的候选直线 如能求a与b的适宜值,能使所有实测值 到这条直线的上纵向距离的平方和为最小 则称这一对a和b为与β的最小二乘估计 least estimation,LES)
三、回归参数的估计 一)回归参数估计的最小二乘原则 参数与一般只能通过样本数据来估计。 当X取值为Xi时,Y的平均值的估计 应为a+bXi ,而实际观察值为Yi。两者之差 称为残差(residual),即 当a与b取不同值时获取不同的候选直线, 如能求a与b的适宜值,能使所有实测值 到这条直线的上纵向距离的平方和为最小, 则称这一对a和b为与的最小二乘估计 (least estimation,LES)。 i y ˆ ( ) i Yi a bXi e = − +

二)回归参数的估计方法=α+bX a为Y轴上的截距;b为斜率,表示X每改变 一个单位,Y的变化的值,称为回归系数;表 示在X值处Y的总体均数估计值。为求a和b两 系数,根据数学上的最小二乘法原理,可导 出a和b的算式如下: 6=∑K-Y-) Σ- a=Y-bX 。-∑x-收-)=∑r-ΣxΣ Σx-y=xx-②x
二)回归参数的估计方法 a为Y轴上的截距;b为斜率,表示X每改变 一个单位,Y的变化的值,称为回归系数;表 示在X值处Y的总体均数估计值。为求a和b两 系数,根据数学上的最小二乘法原理,可导 出a和b的算式如下:

1.由原始数据及散点图的初步分析,本例 呈直线趋势,故作下列计算 2.求 ∑X∑r∑X∑∑Y ∑X=14.7,∑Y=224,∑X2=14.81 ∑r2=3368,∑7=216.5。 3.计算X、Y的均数,及离均差平方和xX yy与离均差积和xw。 1-zx-对=x区y-1481 4.72 =0.404 n 15
1.由原始数据及散点图的初步分析,本例 呈直线趋势,故作下列计算。 2.求 3.计算X、Y的均数,及离均差平方和lXY、 lyy与离均差积和lXY