
第十三章 多重线性回归与相关 多重▣归(multiple linear regression)与多 重相关(multiple correlation)是研究一个因变 量和多个自变量之间线性关系的统计学分析 方法。本章任务是讨论多重回归与相关的 些基本概念,掌握如何收集准确的数据、录 入、正确地调用统计分析程序以及对输出结 果做出合适解释的技能。 第一节多元线性回归的概念与统计描述
第十三章 多重线性回归与相关 多重回归(multiple linear regression)与多 重相关(multiple correlation)是研究一个因变 量和多个自变量之间线性关系的统计学分析 方法。本章任务是讨论多重回归与相关的一 些基本概念,掌握如何收集准确的数据、录 入、正确地调用统计分析程序以及对输出结 果做出合适解释的技能。 第一节 多元线性回归的概念与统计描述

数据与模型 例13-1为了研究空气中一氧化氮(NO)的浓 度与汽车流量等因素的关系,有人测定了某 城市交通点在单位时间内过往的汽车数、 气 温、空气湿度、风速及空气中的一氧化氮 (NO)的浓度,数据如表13-1所示。 此型资料有一个应变量与多个自变量(k个 自变量)依存在关系,它的基本形式为 Y=Bo+BX+B2X2i+…B kXki+。B,为▣ 归方程的常数项,B为偏回归系数 PARTIAL REGRESSION I COEFFICIEBT 相应的由样本估计而得的多重线性回归方程 为; Y=bo+bX+b2x2+..bxXk
一、数据与模型 例13-1 为了研究空气中一氧化氮(NO)的浓 度与汽车流量等因素的关系,有人测定了某 城市交通点在单位时间内过往的汽车数、气 温、空气湿度、风速及空气中的一氧化氮 (NO)的浓度,数据如表13-1所示。 此型资料有一个应变量与多个自变量(k个 自变量)依存在关系,它的基本形式为 Y=0+ 1X1i+ 2X2i+… kXki+i。B0为回 归方程的常数项,Bj为偏回归系数 (PARTIAL REGRESSION COEFFICIEBT) 相应的由样本估计而得的多重线性回归方程 为: Y b b X b X bk Xk ... ˆ = 0 + 1 1 + 2 2 +
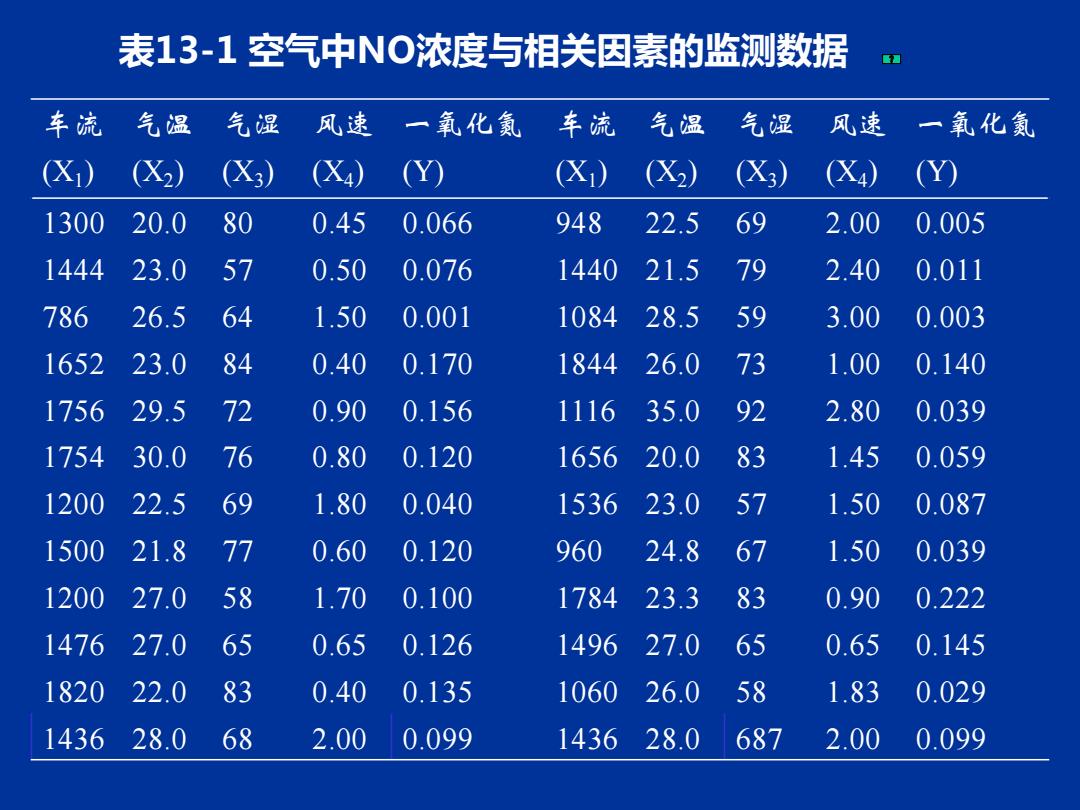
表13-1空气中NO浓度与相关因素的监测数据 车流气温气湿 风速一氧化氮 车流气温气湿 风速 一氧化氮 (X) (X2 X3) (X4) (Y) (Xi (X2 X3) (X4 Y 1300 20.0 80 0.45 0.066 948 22.5 69 2.00 0.005 1444 23.0 57 0.50 0.076 1440 21.5 79 2.40 0.011 786 26.5 64 1.50 0.001 1084 28.5 59 3.00 0.003 1652 23.0 84 0.40 0.170 1844 26.0 73 1.00 0.140 1756 29.5 72 0.90 0.156 1116 35.0 92 2.80 0.039 1754 30.0 76 0.80 0.120 1656 20.0 83 1.45 0.059 1200 22.5 69 1.80 0.040 1536 23.0 57 1.50 0.087 1500 21.8 77 0.60 0.120 960 24.8 67 1.50 0.039 1200 27.0 58 1.70 0.100 1784 23.3 83 0.90 0.222 1476 27.0 65 0.65 0.126 1496 27.0 65 0.65 0.145 1820 22.0 83 0.40 0.135 1060 26.0 58 1.83 0.029 1436 28.0 68 2.00 0.099 143628.0 687 2.00 0.099
车流 气温 气湿 风速 一氧化氮 车流 气温 气湿 风速 一氧化氮 (X1 ) (X2 ) (X3 ) (X4 ) (Y) (X1 ) (X2 ) (X3 ) (X4 ) (Y) 1300 20.0 80 0.45 0.066 948 22.5 69 2.00 0.005 1444 23.0 57 0.50 0.076 1440 21.5 79 2.40 0.011 786 26.5 64 1.50 0.001 1084 28.5 59 3.00 0.003 1652 23.0 84 0.40 0.170 1844 26.0 73 1.00 0.140 1756 29.5 72 0.90 0.156 1116 35.0 92 2.80 0.039 1754 30.0 76 0.80 0.120 1656 20.0 83 1.45 0.059 1200 22.5 69 1.80 0.040 1536 23.0 57 1.50 0.087 1500 21.8 77 0.60 0.120 960 24.8 67 1.50 0.039 1200 27.0 58 1.70 0.100 1784 23.3 83 0.90 0.222 1476 27.0 65 0.65 0.126 1496 27.0 65 0.65 0.145 1820 22.0 83 0.40 0.135 1060 26.0 58 1.83 0.029 1436 28.0 68 2.00 0.099 1436 28.0 687 2.00 0.099 表13-1 空气中NO浓度与相关因素的监测数据

因为k个自变量都具有各自的计量单位及不 同的变异度,所以不能直接用普通偏回归系 数的数值大小来反映各个自变量对反应变量Y 的贡献大小。为此将原始观测数据进行标准 化转换,即: X"=X-X 然后用标准化数据进行回归模型拟合,此时 所获得的回归系数,记为P1P2,P3,Pk,标准 化偏回归系数(standardized partial regression coefficient)又称通径系数(path coefficient)。标准化偏回归系数P较大的自 变量在数值上对反应变量Y的贡献较大
因为k个自变量都具有各自的计量单位及不 同的变异度,所以不能直接用普通偏回归系 数的数值大小来反映各个自变量对反应变量Y 的贡献大小。为此将原始观测数据进行标准 化转换,即: 然后用标准化数据进行回归模型拟合,此时 所获得的回归系数,记为P1 ,P2 ,P3 ,…,Pk ,标准 化偏回归系数(standardized partial regression coefficient)又称通径系数(path coefficient)。标准化偏回归系数Pi较大的自 变量在数值上对反应变量Y的贡献较大。 i i i i S X X X − = *

二、回归参数的估计 多元线性回归方程的建立(利用最小二乘 法的原理)Q=Σ6-) 虽然多重回归参数估计的原理和方法与简 单回归分析相同,但是随着自变量个数的增 加计算量变得相当大,一般依软件包来完成。 对于本例的数据,经软件包计算可得回归方 程 )=-0.14166+0.00011619X,+0.0049X -0.00000655X3-0.03468X4
二、回归参数的估计 多元线性回归方程的建立(利用最小二乘 法的原理) 虽然多重回归参数估计的原理和方法与简 单回归分析相同,但是随着自变量个数的增 加计算量变得相当大,一般依软件包来完成。 对于本例的数据,经软件包计算可得回归方 程: ( ) 2 Q = y − y ˆ 3 4 1 2 0.00000655 0.03468 ˆ 0.14166 0.00011619 0.0049 X X y X X − − = − + +
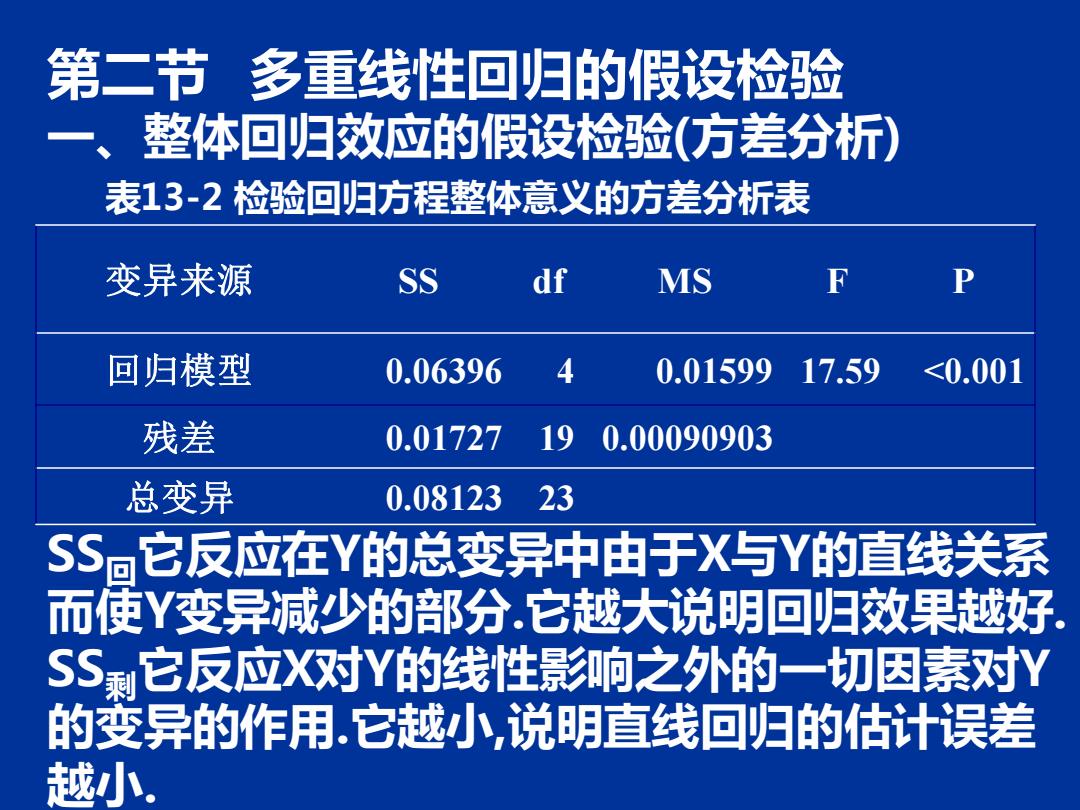
第二节多重线性回归的假设检验 一、整体回归效应的假设检验(方差分析) 表13-2检验回归方程整体意义的方差分析表 变异来源 SS df MS P 回归模型 0.06396 44 0.01599 17.59 <0.001 残差 0.01727 19 0.00090903 总变异 0.08123 23 SS▣它反应在Y的总变异中由于X与Y的直线关系 而使Y变异减少的部分.它越大说明回归效果越好 SS剩它反应X对Y的线性影响之外的一切因素对Y 的变异的作用.它越小,说明直线回归的估计误差 越小
第二节 多重线性回归的假设检验 一、整体回归效应的假设检验(方差分析) 表13-2 检验回归方程整体意义的方差分析表 SS回它反应在Y的总变异中由于X与Y的直线关系 而使Y变异减少的部分.它越大说明回归效果越好. SS剩它反应X对Y的线性影响之外的一切因素对Y 的变异的作用.它越小,说明直线回归的估计误差 越小. 变异来源 SS df MS F P 回归模型 0.06396 4 0.01599 17.59 <0.001 残差 0.01727 19 0.00090903 总变异 0.08123 23

二、偏回归系数β的假设检验 1.假设 H。:B=0,H1:B≠0,a=0.05 2.检验统计量 --0 v=1 利用软件包对例13-3的四个偏回归系数进行检 验与标准化偏回归系数的结果如表13-3所示
二、偏回归系数i的假设检验 1.假设 2.检验统计量 利用软件包对例13-3的四个偏回归系数进行t检 验与标准化偏回归系数的结果如表13-3所示
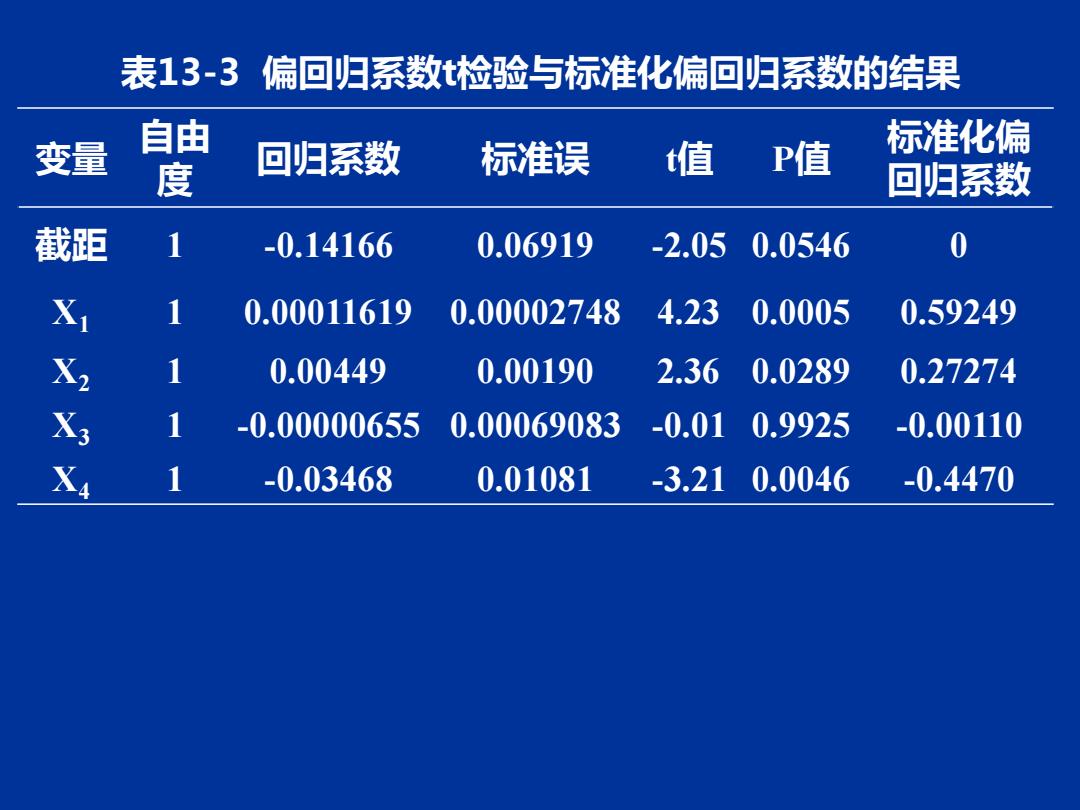
表13-3 偏回归系数t检验与标准化偏回归系数的结果 变量 自由 标准化偏 度 回归系数 标准误 值P值 回归系数 截距 1 -0.14166 0.06919 -2.05 0.0546 0 1 0.00011619 0.00002748 4.23 0.0005 0.59249 1 0.00449 0.00190 2.36 0.0289 0.27274 1 0.00000655 0.00069083 -0.010.9925 -0.00110 1 -0.03468 0.01081 -3.210.0046 0.4470
表13-3 偏回归系数t检验与标准化偏回归系数的结果 变量 自由 度 回归系数 标准误 t值 P值 标准化偏 回归系数 截距 1 -0.14166 0.06919 -2.05 0.0546 0 X1 1 0.00011619 0.00002748 4.23 0.0005 0.59249 X2 1 0.00449 0.00190 2.36 0.0289 0.27274 X3 1 -0.00000655 0.00069083 -0.01 0.9925 -0.00110 X4 1 -0.03468 0.01081 -3.21 0.0046 -0.4470

第三节 复相关系数与偏相关系数 一、确定系数、 复相关系数与调整确定系数 复相关系数的平方称为确定系数(coefficient of determination),或决定系数,记为R2,用 于反映线性回归模型能在多大程度上解释反应 变量Y的变异性。定义为R2=SSR/SST. 它的取值范围为0-1之间。它越接近1,表示样 本数据很好地拟合了所选用线性回归模型。R2 直接反映了回归方程中所有自变量解释反应变 量Y总变异的百分比,或者说,R也可以解释 为回归方程使反应变量Y的总变异减少的百分比
第三节 复相关系数与偏相关系数 一、确定系数、复相关系数与调整确定系数 复相关系数的平方称为确定系数(coefficient of determination),或决定系数,记为R2,用 于反映线性回归模型能在多大程度上解释反应 变量Y的变异性。定义为R2=SSR/SST. 它的取值范围为0-1之间。它越接近1,表示样 本数据很好地拟合了所选用线性回归模型。 R2 直接反映了回归方程中所有自变量解释反应变 量Y总变异的百分比,或者说, R2也可以解释 为回归方程使反应变量Y的总变异减少的百分比

对总体确定系数R2=0的假设检验完全 等价于对回归方程的整体方差分析,因为 MSR SSR R2 MSE SSE n-k-1) 1-R2 对例13-1,由方差分析表可得 (n-k-1) SSR=0.06396SSE=0.01727 SST=0.08123 R2=0.06396/0.08123=1- 0.01272/0.08123= 0.7874.由此说明,用包含汽车流量、气
对总体确定系数R2=0的假设检验完全 等价于对回归方程的整体方差分析,因为 对例13-1,由方差分析表可得: SSR=0.06396 SSE=0.01727 SST=0.08123 R2=0.06396/0.08123=1- 0.01272/0.08123= 0.7874.由此说明,用包含汽车流量、气 温、气湿与风速这四个自变量的回归方程 ( ) ( ) ( 1) 1 1 2 2 − − − = − − = = n k R k R n k SSE k SSR MSE MSR F