
Van der Waals状态方程式 1.物化原理 实际气体在an der Waals状态方程式: p+品C.-b=RT (1.1) 展开后为摩尔体积V的三次方程式: 以-+gg+g.g0 (12) p 对此非线性三次方程式,可借助于Newton--Raphson迭代法近似求解 2.Newton--Raphson迭代法原理 给定初值a,对方程f(x)=0进行Taylor展开: f=)+-',+x-xf)++x-rf) 忽略二阶以上(仁x-x)误差项,得: f(x)=f(x)+(x-x)f'(x)=0 f"(x。 代入得: 周 式中x为第一次迭代值,作为下一迭代初值,经过次迭代后,方程的根 f() x.=) 本题中x为实际气体摩尔体积Vm。 迭代公式如下: Vi=Vi- f) (3) ) 式子中V,是经过第i次选代后的摩尔体积,V1是经过第+1次迭代后的摩尔体积,f(V, 是第I次迭代后方程式(2)的值,f(V)是第I+1次迭代后方程式(2)的值。V的初 始值?选理想气休的值,即:?= ,反复用(3)式迭代求出接近真值的根。本题误 p
Van der Waals 状态方程式 1. 物化原理 实际气体在 Van der Waals 状态方程式: (V b) RT V a p m m - = ÷ ÷ ø ö ç ç è æ + 2 (1.1) 展开后为摩尔体积 Vm的三次方程式: ( ) ( ) 0 3 2 = - + + - = p ab V p RT V p RT f V V b m m m (1.2) 对此非线性三次方程式,可借助于 Newton-Raphson 迭代法近似求解, 2. Newton-Raphson 迭代法原理 给定初值 x0,对方程 f(x)=0 进行 Taylor 展开: ( ) ( ) ! 1 ( ) ( ) ... 2! 1 ( ) ( ) ( ) ( ) 0 0 0 2 // 0 0 / 0 0 x x f x n f x f x x x f x x x f x n n = + - + - + + - 忽略二阶以上 ( ) 0 0 e = x - x 误差项,得: ( ) ( ) ( ) ( ) 0 0 / f x = f x0 + x - x0 f x = 即: ( ) ( ) 0 / 0 0 f x f x e = 代入得: ( ) ( ) 0 / 0 0 f x f x x = x - 式中 x 为第一次迭代值,作为下一迭代初值,经过 n 次迭代后,方程的根: ( ) ( ) 1 / 1 1 - - = - - n n n n f x f x x x 本题中 x 为实际气体摩尔体积 Vm。 迭代公式如下: ( ) ( ) 1 / i i i i f V f V V + = V - (3) 式子中 Vi是经过第 i 次迭代后的摩尔体积,Vi+1是经过第 I+1 次迭代后的摩尔体积,f(Vi) 是第 I 次迭代后方程式(2)的值,f /(Vi)是第 I +1 次迭代后方程式(2)的值。Vm的初 始值 0 Vm 选理想气体的值,即: p RT Vm = 0 ,反复用(3)式迭代求出接近真值的根。本题误
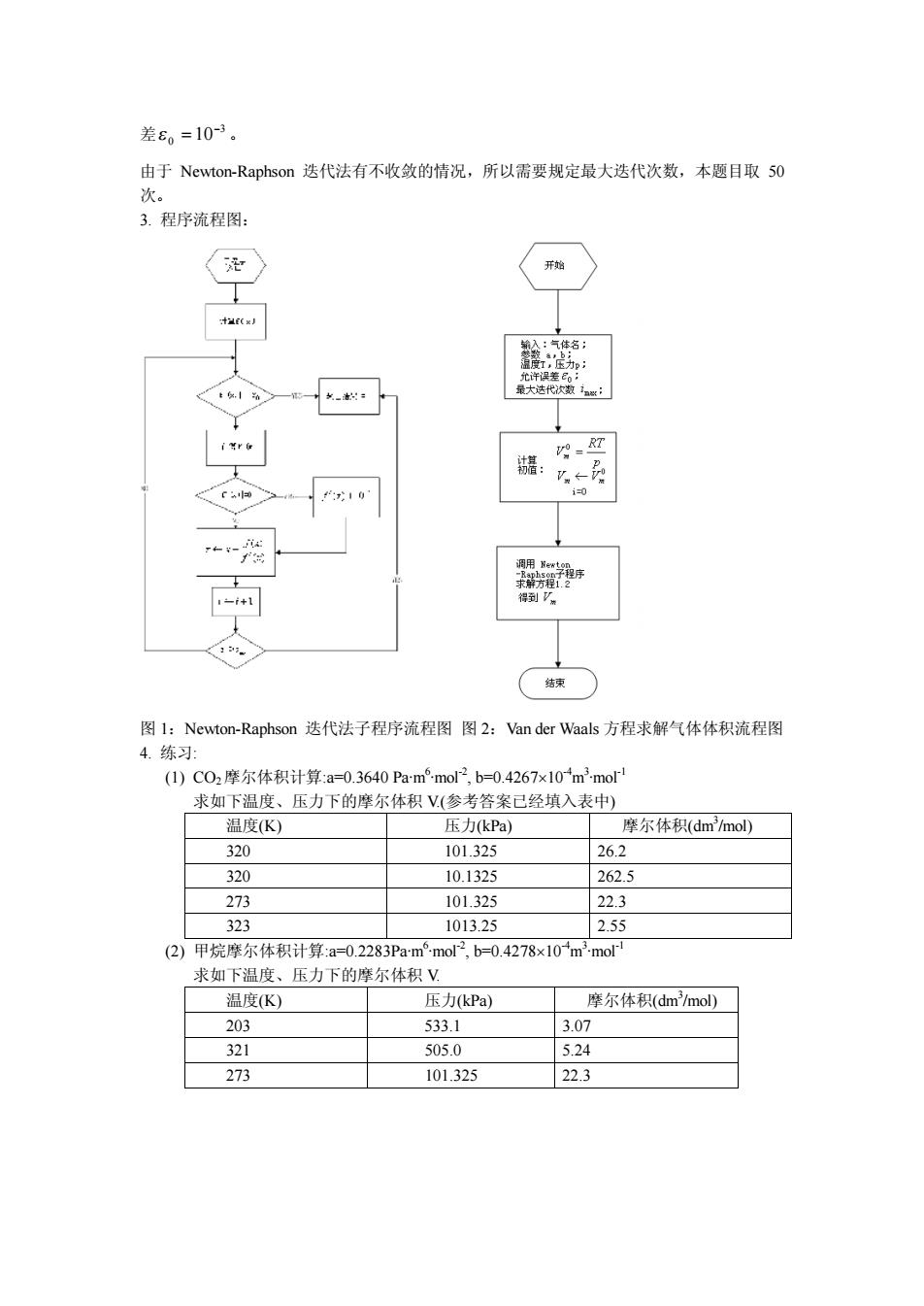
差8。=103。 由于Newtom-Raphson选代法有不收敛的情况,所以需要规定最大迭代次数,本题目取50 次 3.程序流程图: 、 图l:Newton-Raphson迭代法子程序流程图图2:Van der Waals方程求解气体体积流程图 4.练习: ()C02摩尔体积计算a=0.3640Pam°mol2,b=0.4267x10m2mor 求如下温度、压力下的摩尔体积V(参考答案己经填入表中) 温度(K 压力kP阿 摩尔体积dm'/mol) 320 101.325 26.2 320 10.1325 262.5 273 101325 223 323 101325 (2)甲烷摩尔体积计算:a=0.2283Pam°mol2,b-0.4278×10'mmo 求如下温度、压力下的摩尔体积V 温度(K) 压力Pa 摩尔体积(dm/mol) 2 533.1 3.0 321 505.0 5.24 273 101.325 22.3
差 3 0 10- e = 。 由于 Newton-Raphson 迭代法有不收敛的情况,所以需要规定最大迭代次数,本题目取 50 次。 3. 程序流程图: 图 1:Newton-Raphson 迭代法子程序流程图 图 2:Van der Waals 方程求解气体体积流程图 4. 练习: (1) CO2摩尔体积计算:a=0.3640 Pa·m 6 ·mol-2, b=0.4267´10-4 m 3 ·mol-1 求如下温度、压力下的摩尔体积 V.(参考答案已经填入表中) 温度(K) 压力(kPa) 摩尔体积(dm3 /mol) 320 101.325 26.2 320 10.1325 262.5 273 101.325 22.3 323 1013.25 2.55 (2) 甲烷摩尔体积计算:a=0.2283Pa·m 6 ·mol-2, b=0.4278´10-4 m 3 ·mol-1 求如下温度、压力下的摩尔体积 V. 温度(K) 压力(kPa) 摩尔体积(dm3 /mol) 203 533.1 3.07 321 505.0 5.24 273 101.325 22.3