
半衰期法确定化学反应动力学方程 一、原理 动力学方程式: de-ke (1D d 当n≠1时,反应半衰期12与起始浓度c10:反应级数n之间的关系为: 12--1 tv:=K(n-1)e. (2) 对温度一定的某反应m,k为定值,对(2)取对数得一线性方程: Intuz =In B-(n-1)Inco n-为定值。 n12~nc4o图为一条直线,斜率Sl-n。由截距lnB求出B,进而求出速率常数k。 因为1级反应12与ca0无关,nL2~nco图为一条水平直线,斜率为0. 所以该法对一级反应来说,求反应级数时仍然适用,求速率常数k时直接用公式 k=In2 实验数据主要分两种情况: (I)如果实验测得若干起始浓度cao所对应的半衰期1,2,直接将nv2对进行 线性回归得到反应级数n和速率常数k。 (2)如果实验仅测定了一个反应物起始浓度下不同时间t对应的反应物浓度C4,可用 任一浓度ca作为起始浓度,用Lagrange插值法求出此浓度降低一半所需的时间间隔作为 c么。=c4时的半衰期,·再按照情况(1)的方法进行线性回归。 二、流程图
半衰期法确定化学反应动力学方程 一、原理 动力学方程式: A n A kc dt dc - = (1) 当 n ¹ 1时,反应半衰期 1/ 2 t 与起始浓度 cA,0,反应级数 n 之间的关系为: 1 1 1/ 2 ,0 2 1 ( 1) 1 - - - - = n n A k n c t (2) 对温度一定的某反应 n,k 为定值,对(2)取对数得一线性方程: 1/ 2 ,0 ln ln ( 1)ln A t = B - n - c 上式 ( 1) 2 1 1 - - = - k n B n ,为定值。 1/ 2 ,0 ln ~ ln A t c 图为一条直线,斜率 S=1-n。由截距ln B 求出 B,进而求出速率常数 k。 因为 1 级反应 1/ 2 t 与 cA,0 无关, 1/ 2 ,0 ln ~ ln A t c 图为一条水平直线,斜率为 0。 所以该法对一级反应来说,求反应级数时仍然适用,求速率常数 k 时直接用公式 1/ 2 ln 2 t k = 。 实验数据主要分两种情况: (1)如果实验测得若干起始浓度 cA,0 所对应的半衰期 1/ 2 t ,直接将 1/ 2 ln t 对 ,0 ln A c 进行 线性回归得到反应级数 n 和速率常数 k。 (2)如果实验仅测定了一个反应物起始浓度下不同时间 t 对应的反应物浓度 cA, 可用 任一浓度 cA 作为起始浓度,用 Lagrange 插值法求出此浓度降低一半所需的时间间隔作为 A A c = c / ,0 时的半衰期 / 1 / 2 t 。再按照情况(1)的方法进行线性回归。 二、流程图
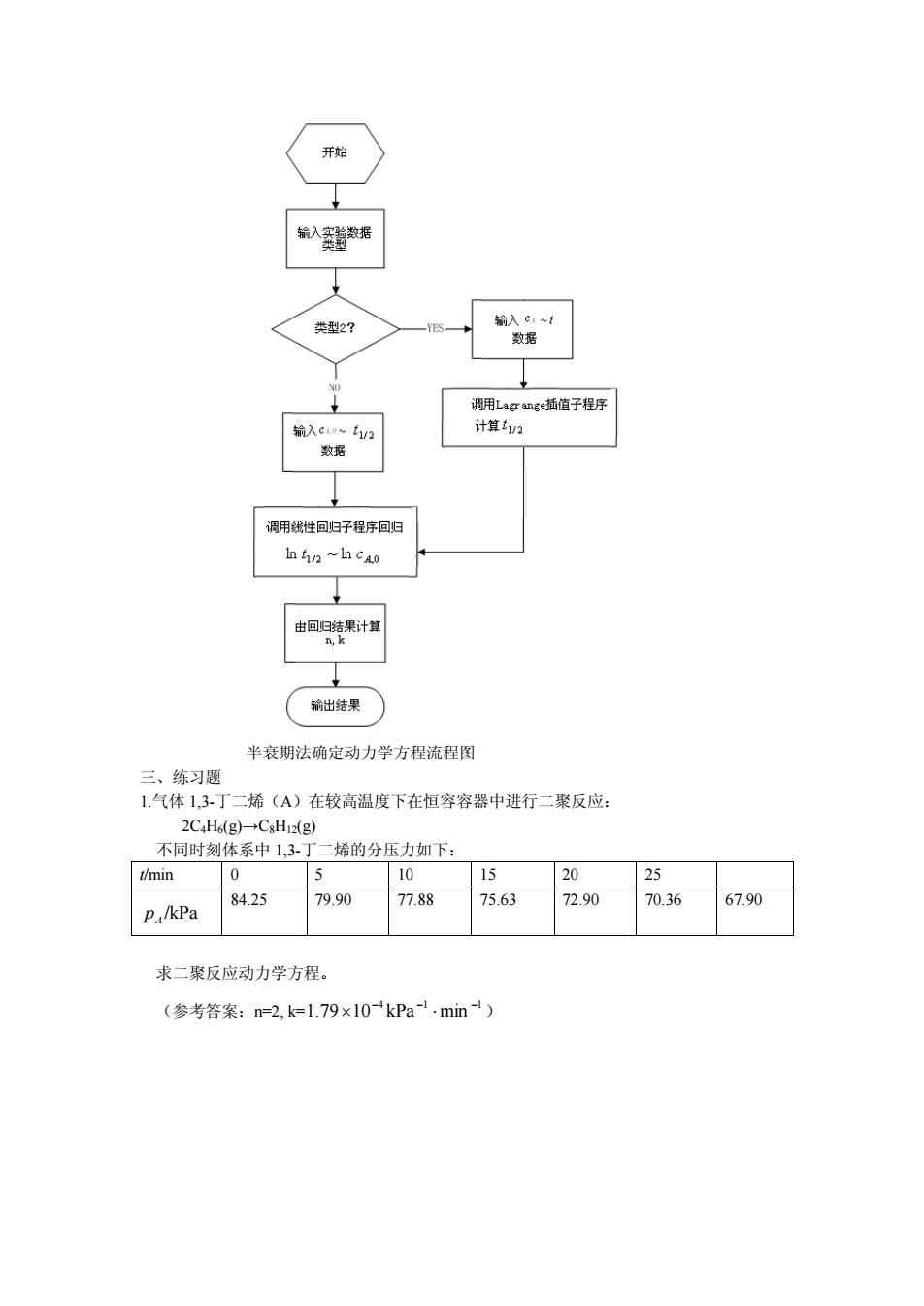
g插值子程 用性回子程序回 翰出结果 半衰期法确定动力学方程流程图 三、练习题 1.气体1,3丁二烯(A)在较高温度下在恒容容器中进行二聚反应: 2C.H(g)-CxH:(g) 不同时刻体系中1,3丁二烯的分压力如下: t/min 0 5 10 15 20 25 84.25 79.90 P./kPa 77.88 75.63 72.90 70.36 67.90 求二聚反应动力学方程。 (参考答案:n=2,k=1.79×10kPa1.min-)
半衰期法确定动力学方程流程图 三、练习题 1.气体 1,3-丁二烯(A)在较高温度下在恒容容器中进行二聚反应: 2C4H6(g)→C8H12(g) 不同时刻体系中 1,3-丁二烯的分压力如下: t/min 0 5 10 15 20 25 /kPa A p 84.25 79.90 77.88 75.63 72.90 70.36 67.90 求二聚反应动力学方程。 (参考答案:n=2, k= 4 1 1 1.79 10 kPa min - - - ´ × )