
压力对平衡转化率的影响 一、原理 1.物化原理 任何化学反应达到平衡时有: ∑Vg4B=0 当发生一个单元反应时,设A的转化率为x: aA bB +...cC +dD 0 0 b(I-x) ex 学 平衡时的总摩尔数∑nB=△x+n 式子中:△v=∑ye m。=a+b+=-∑y(饭应物) 平衡常数K,与系统p关系为: K-K(pa) 如果条件中给出的是K9,它与K,的关系为:K,=K,(p),(pP为100kP) 平衡转化率与总压之间解析式: 令: Pa 令: ∑na K=0 这是一个含X的高次方程式,平衡转化率X=0.01.0之间一定有一实根,因此对此方程用对 分法求解比较简便。 2对分法原理
压力对平衡转化率的影响 一、原理 1.物化原理 任何化学反应达到平衡时有: ån B mB = 0 当发生一个单元反应时,设 A 的转化率为 x: aA + bB +…= cC + dD +…. t=0 a b 0 0 t=t a(1-x) b(1-x) cx dx 平衡时的总摩尔数 n0 n x å B = Dn + 式子中: Dn = ån B = + + = -å (反应物) n a b n B ... 0 平衡常数 Kp与系统 p 关系为: Kp=Ky ( ) Dn p总 = ( ) a b c d B a b c d a b c d n p x x Dn + + ÷ ÷ ø ö ç ç è æ - å 总 1 如果条件中给出的是 Kp y,它与 Kp的关系为: Kp= Kp y(py) Δν , (py为 100kPa) 平衡转化率与总压之间解析式: ( ) c d a b B a b p c d c d a b p n K x x Dn + + ÷ ÷ ø ö ç ç è æ = - å 1 总 令: c d n a b K c d a b = ( ) n B a b p c d K p n K x x Dn + + ÷ ÷ ø ö ç ç è æ = - å 1 总 令: ( ) 0 1 ( ) = ÷ ÷ ø ö ç ç è æ - - = D + + å n B a b p c d K p n K x x F X n 总 …….. (1) 这是一个含 X 的高次方程式,平衡转化率 X=0.0-1.0 之间一定有一实根,因此对此方程用对 分法求解比较简便。 2.对分法原理

有方程f(X)0,求在区间[a,b]内的实根。 设:(1)方程f(X)0内连续: (2)函数在a、b两点之间f(X)异号,说明f(X)=0区间a,b内至少有一个实根 计算步骤 ()X的初值,术。=a牛也(对分) 计算函数f(X)值,若f(X。<e,(e为10)则X为方程所求之根,否则: (2)如果f(X)与f(a)异号,取a,为新的区间,如果f()与f(b)异号,取 [X,b为新的区间。新的区间统标记为区间[,b小,然后按照如上“1.”的方法 进行。 即:X,+X,a+ 2 计算函数f(X)值,若f(X,<8,则X为方程所求之根,否则令[a,X]或[X,b 为新的区间继续执行… 在以上执行过程中,可得到一系列区间套: (an.ba)c (an1,ba)c...(ai,b)c (a,b) (f(a,)f(b)< 它们必须满足: 如果要求的实根的绝对值不超过,则只要n充分大时,必然有 此时区间(a,b)上任一点都可作为所求的近似根。 为了防止函数曲线过陡,用F(X)判断有时不易于收敛,因而加入 b,-an≤8 进行判断,以保证更易收敛。 二、程序流程图
有方程 f(X)=0,求在区间[a,b]内的实根。 设:(1)方程 f(X)=0 内连续; (2)函数在 a、b 两点之间 f(X)异号,说明 f(X)=0 区间[a,b]内至少有一个实根。 计算步骤: (1) X 的初值, 2 0 a b X + = (对分) 计算函数 f(X0)值,若 ( ) , 0 f X < e (ε 为 10-5)则 X0为方程所求之根,否则: (2) 如果 f(X0)与 f(a)异号,取[a,X0]为新的区间,如果 f(X0)与 f(b)异号,取 [X0,b]为新的区间。新的区间统标记为区间[a1,b1],然后按照如上“1. ”的方法 进行。 即: 2 0 1 X b X + = 或 2 1 1 a X X + = 计算函数 f(X1)值,若 ( ) , 1 f X < e 则 X0为方程所求之根,否则令[a1,X1]或[X1,b1] 为新的区间继续执行…… 在以上执行过程中,可得到一系列区间套: (an, bn)Ì(an-1, bn-1)Ì…..Ì(a1, b1)Ì(a, b) 它们必须满足: ï î ï í ì - - = × < n n n n n b a b a f a f b 2 ( ) ( ) 0 如果要求的实根的绝对值不超过 ε,则只要 n 充分大时,必然有: < e - - = 2 b a b a n n 此时区间(an, bn)上任一点都可作为所求的近似根。 为了防止函数曲线过陡,用|f(X0)|判断有时不易于收敛,因而加入 - £ e n n b a 进行判断,以保证更易收敛。 二、程序流程图
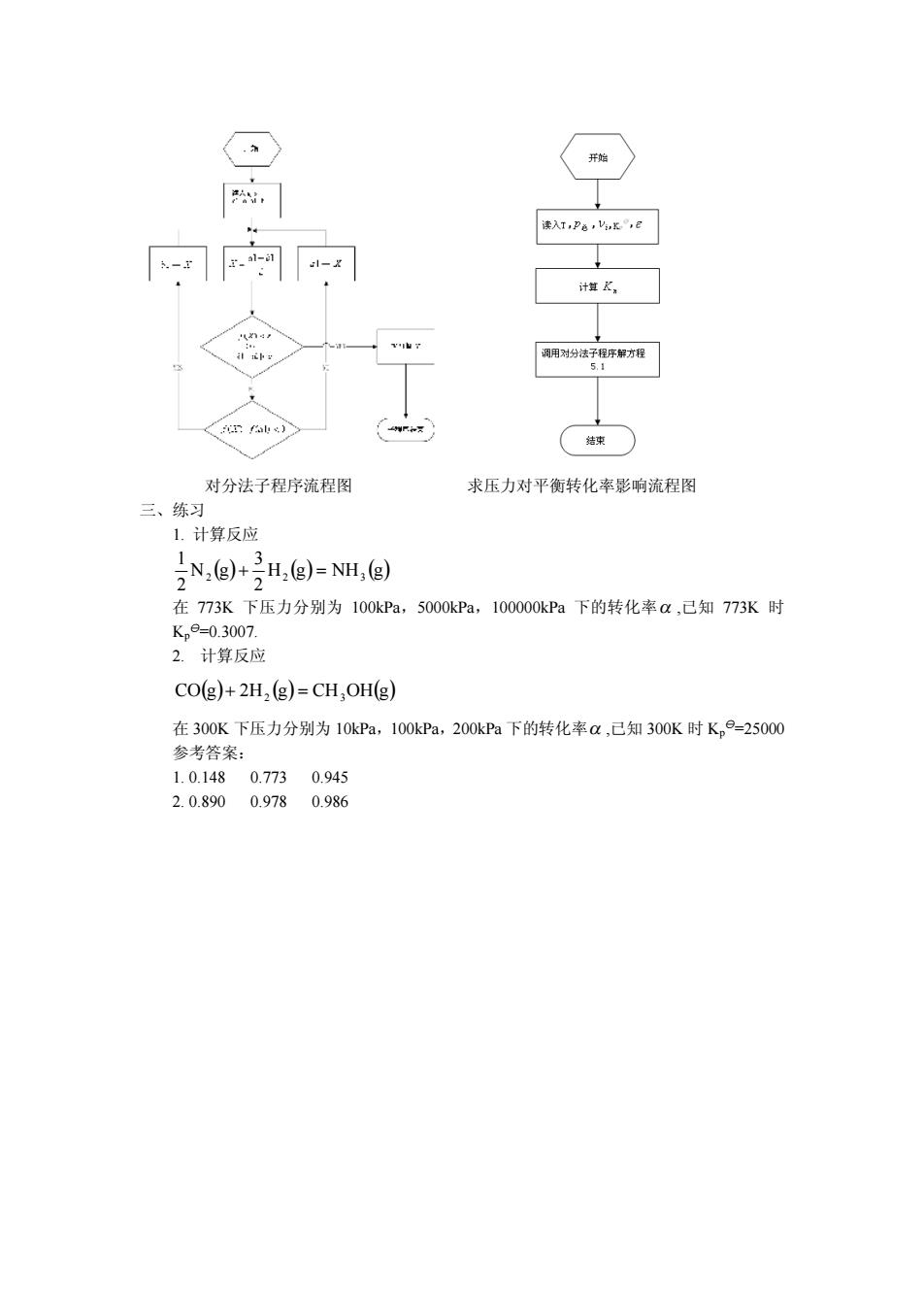
开始 凑入T,Pě,V,K, 计笪K 调用对分法子程序解方程 5.1 nfu) 结束 对分法子程序流程图 求压力对平衡转化率影响流程图 三、练习 1.计算反应 N@-@-N@) 在773K下压力分别为100kPa,5000kPa,100000kPa下的转化率a,已知773K时 K,9=0.3007. 2.计算反应 CO(g)+2H2(g)=CH,OH(g) 在300K下压力分别为10kPa,100kPa,200kPa下的转化率a,已知300K时K,9=25000 参考答案: 1.0.1480.773 0.945 2.0.8900.978 0.986
对分法子程序流程图 求压力对平衡转化率影响流程图 三、练习 1. 计算反应 ( ) H ( ) g NH ( ) g 2 3 N g 2 1 2 + 2 = 3 在 773K 下压力分别为 100kPa,5000kPa,100000kPa 下的转化率a ,已知 773K 时 Kp y=0.3007. 2. 计算反应 CO(g) 2H (g) CH OH(g) + 2 = 3 在 300K 下压力分别为 10kPa,100kPa,200kPa 下的转化率a ,已知 300K 时 Kp y=25000 参考答案: 1. 0.148 0.773 0.945 2. 0.890 0.978 0.986