
克克方程 一、原理 1.物化原理 纯二元气-液、气-周两相平衡方程式一Clausius-Clapeyron方程一是: dinp AH (1) dT RT P为温度T(K)时的液体(固体)饱和蒸汽压,△H为相变热,当温度变化不大时△H可 以看作常数,将①)式取不定积分有:。元片=nB 1 p=-兴}数 (2) (2)式表明,p号呈线性关系,道从y=尔+B线性方程,利用线性回归技术可以 得到A、B。进而得到相变热△H。 2.线性回归原理 函数y=a+b加 式中y和x是由实验测定的值,为确定线性函数中的a和b,采用“最小二乘法”,即 使下式中的各个数据点的残差的平方和最小。 一个数据点的残差:Y,=y-(a+bx,) 使∑y最小的a和b即为所求。设总数据点数为n,∑Y分别对a和b求偏导数 当其为0并且二阶导数为正时,得到极小值。 a∑x -2y-a-bx1-y2-a-bx2]=-2∑y,-2na-2b∑x,=-0 da 整理得到: 含=阳+空x (3) (a∑y2Y 同样,通过 b 0,可以得到 立H=2+空 (4) 联合(3),(4)两式子,得到
克-克方程 一、原理 1. 物化原理 纯二元气-液、气-固两相平衡方程式—Clausius- Clapeyron 方程—是: 2 ln RT H dT d p D = (1) p 为温度 T(K)时的液体(固体)饱和蒸汽压,ΔH 为相变热,当温度变化不大时ΔH 可 以看作常数。将(1)式取不定积分有: i i T x 1 = i i y = ln p + D = - R T H p 1 ln 常数 (2) (2)式表明,lnp ~ T 1 呈线性关系,遵从 y = Ax + B 线性方程。利用线性回归技术可以 得到 A、B。进而得到相变热ΔH。 2. 线性回归原理 函数 y = a + bx 式中 y 和 x 是由实验测定的值,为确定线性函数中的 a 和 b,采用“最小二乘法”,即 使下式中的各个数据点的残差g的平方和最小。 一个数据点的残差: ( ) i i i g = y - a + bx 使å i i 2 g 最小的 a 和 b 即为所求。设总数据点数为 n, å i i 2 g 分别对 a 和 b 求偏导数, 当其为 0 并且二阶导数为正时,得到极小值。 å å å = - - - - - - = - - - ÷ ÷ ÷ ø ö ç ç ç è æ ¶ ¶ i i i i b i i y a bx y a bx y na b x a 2[ 1 1 2 2 .......] 2 2 2 2 g =0 整理得到: å å = = = + n i i n i i y na b x 1 1 (3) 同样,通过 a i i b ÷ ÷ ÷ ø ö ç ç ç è æ ¶ ¶å 2 g =0,可以得到 å å å = = = = + n i n i n i i i i i y x a x b x 1 1 1 2 (4) 联合(3),(4)两式子,得到:

6=g兴,a2y-芝 n∑x2-∑x∑x, n 各个数据点的x,y的平均值 2,之 引入下,后,b表达式可以写成: ∑xy- 6-网 令:∑y2-2=Sm∑x2-m2=Sa∑xy-m呵=Sn 再引入符号SwS,Sw后得到: 定义线性相关系数: R=- ,R越接近1,表示数据点的线性关系越好。 6.5n 二、程序流程图 线性回归流程图 汽化热计算程序流程图
å å å å å - - = i i i i i i i n x x x n x y y x b 2 , n y b x a å i - å i = 各个数据点的 x,y 的平均值: å= = n i i x n x 1 1 , å= = n n i y n y 1 1 引入 x , y 后,b 表达式可以写成: å å - - = 2 2 x nx x y nyx b i i i 令: yy i å y - ny = S 2 2 , xx åxi - nx = S 2 2 , xy i i åx y - nxy = S 再引入符号 Syy,Sxx,Sxy,后得到: xx xy S S b = , a = y - bx 定义线性相关系数: ( )2 1 xx yy xy S S S R = ,R 越接近 1,表示数据点的线性关系越好。 二、程序流程图 线性回归流程图 汽化热计算程序流程图
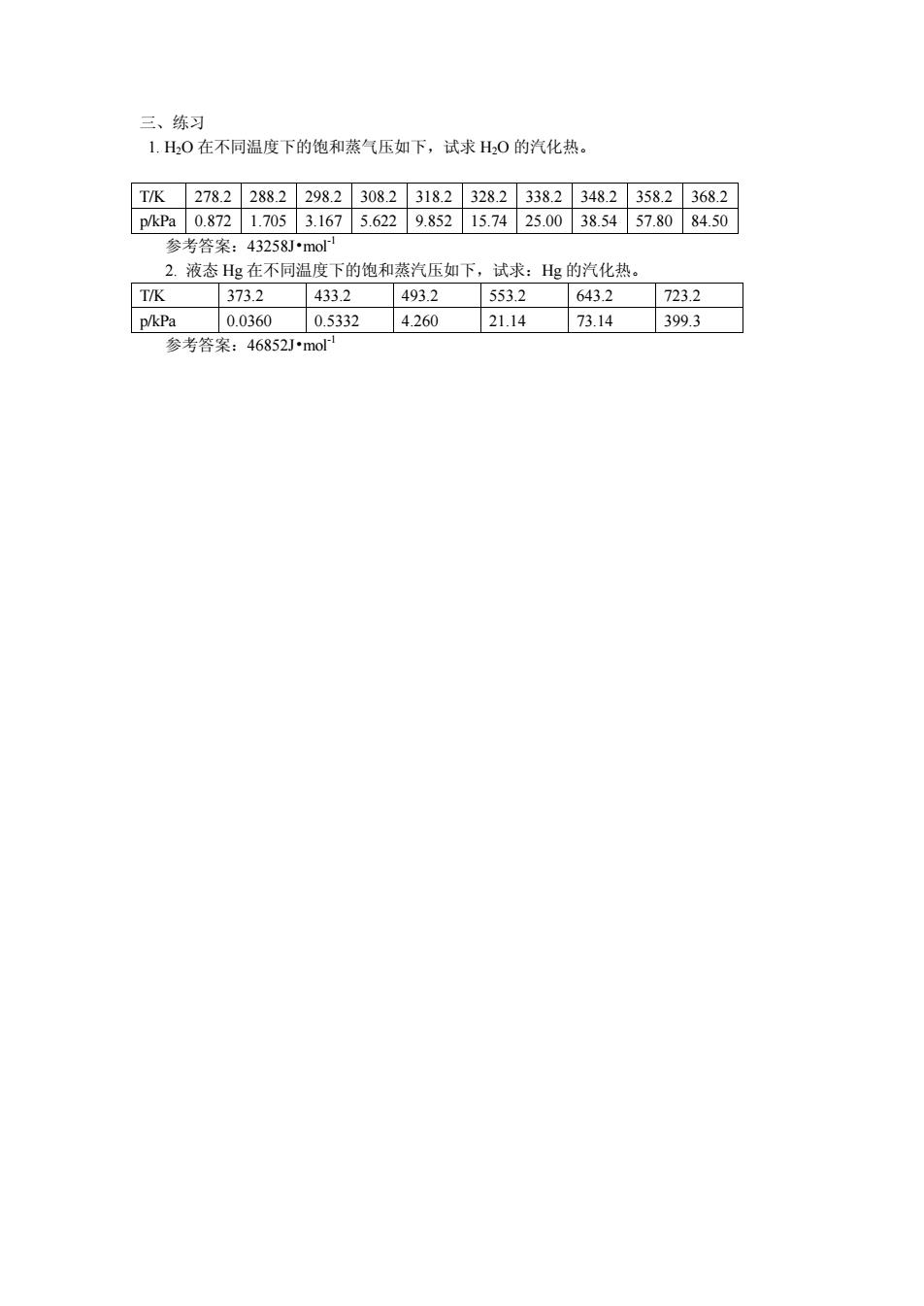
三、练习 1.H0在不同温度下的饱和蒸气压如下,试求H,0的汽化热。 TK27822882298.23082318.2328233823482358.23682 pkPa0.8721.7053.1675.6229.85215.7425.0038.5457.8084.50 参考答案:43258Jmo 2.液态Hg在不同温度下的饱和蒸汽压如下,试求:Hg的汽化热。 TK373.2 433.2 493.2 553.2 643.2 723.2 pkPa0.03600.53324.26021.1473.14399.3 参考答案:46852Jmo
三、练习 1. H2O 在不同温度下的饱和蒸气压如下,试求 H2O 的汽化热。 T/K 278.2 288.2 298.2 308.2 318.2 328.2 338.2 348.2 358.2 368.2 p/kPa 0.872 1.705 3.167 5.622 9.852 15.74 25.00 38.54 57.80 84.50 参考答案:43258J•mol-1 2. 液态 Hg 在不同温度下的饱和蒸汽压如下,试求:Hg 的汽化热。 T/K 373.2 433.2 493.2 553.2 643.2 723.2 p/kPa 0.0360 0.5332 4.260 21.14 73.14 399.3 参考答案:46852J•mol-1