
实际气体逸度的计算 一、原理 1.物化原理 纯气体逸度由定义得到: dμ=RTdIn f=Vdp () V为实际气体体积,设α为理想气体与实际气体体积在同温同压下的差,有: v- (2) 代入(1)试有: 理塑气传,加p=g中 (3) (1)式减去(3)式,再积分得: g 2.数学原理 Simpson法利用一个插值多项式来近似表示被积函数,把积分空间分割成有限个小区 间,在每个区间上采用二次抛物线近似被积函数的图形,近似小区间面积,然后将有限个小 区间相加得到被积函数的近似值。 对于积分广x)水,将积分区间[a,]分成2n等份,每个区间宽h=6-口,每个小 区间中用Lagrange多项式来近似表示被积函数。 Lagrange多项式 一元三点不等距插值。 m-8器 ⑤) j=l 11-x<+,x20=23-2 2 i=n-2:r≥+x2 2 利用插值公式近似求出小区间的面积,再对整个区间求和的Simpson公式为:
实际气体逸度的计算 一、原理 1. 物化原理 纯气体逸度由定义得到: dm = RTd ln f = Vdp (1) V 为实际气体体积,设a 为理想气体与实际气体体积在同温同压下的差,有: = -a p RT V (2) 代入(1)式有: 理想气体: dp p RT RTd ln p = (3) (1)式减去(3)式,再积分得: dp p RT f p ò = - 0 ln a (4) p f 是逸度系数,用j 表示。纯气体逸度用j × p计算。j 通过求(4)式中的积分计算。 2. 数学原理 Simpson 法利用一个插值多项式来近似表示被积函数,把积分空间分割成有限个小区 间,在每个区间上采用二次抛物线近似被积函数的图形,近似小区间面积,然后将有限个小 区间相加得到被积函数的近似值。 对于积分ò b a f (x)dx ,将积分区间[a,b]分成 2n 等份,每个区间宽 n b a h 2 - = ,每个小 区间中用 Lagrange 多项式来近似表示被积函数。 Lagrange 多项式:一元三点不等距插值。 å Õ + = + ¹ = - - = = 2 2 ( ) ( ) i j i i k j k i j k k j x x x x f x y x y (5) ;( 2,3,..., 2) 2 ,且 2 1; 1 1 2 = - + ³ + = - < - - - l n x x x x x i l x l l l l 2 2; -1 + -2 = - ³ n n x x i n x 利用插值公式近似求出小区间的面积,再对整个区间求和的 Simpson 公式为:
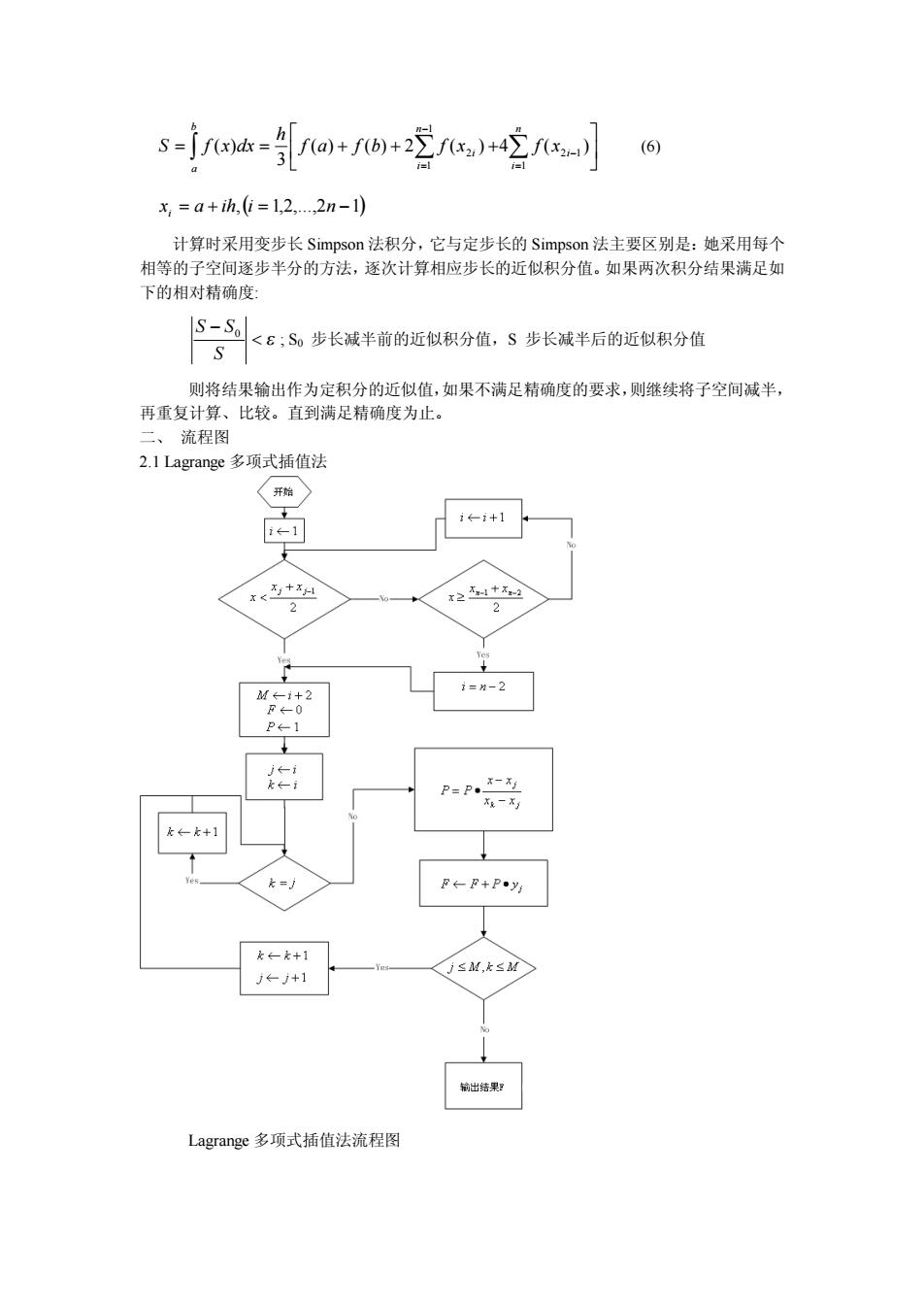
sjoh-@++2)+空- x,=a+h,=12…2n-1 计算时采用变步长Simpson法积分,它与定步长的Simpson法主要区别是:她采用每个 相等的子空间逐步半分的方法,逐次计算相应步长的近似积分值。如果两次积分结果满足如 下的相对精确度 下6:。步长减半前的近似积分值,S步长减半后的近似积分值 S-So 则将结果输出作为定积分的近似值,如果不满足精确度的要求,则继续将子空间减半, 再重复计算、比较。直到满足精确度为止。 流程图 2.1 Lagrange多项式插值法 开 ←1+1 ←1 x+ F←F+Py -+1 出结知 Lagrang心多项式插值法流程图
ò å å ú û ù ê ë é = = + + + = - - = b a n i i n i i f a f b f x f x h S f x dx 1 2 1 1 1 2 ( ) ( ) 2 ( ) 4 ( ) 3 ( ) (6) x = a + ih,(i = 1,2,...,2n -1) i 计算时采用变步长 Simpson 法积分,它与定步长的 Simpson 法主要区别是:她采用每个 相等的子空间逐步半分的方法,逐次计算相应步长的近似积分值。如果两次积分结果满足如 下的相对精确度: < e - S S S0 ; S0 步长减半前的近似积分值,S 步长减半后的近似积分值 则将结果输出作为定积分的近似值,如果不满足精确度的要求,则继续将子空间减半, 再重复计算、比较。直到满足精确度为止。 二、 流程图 2.1 Lagrange 多项式插值法 Lagrange 多项式插值法流程图

2.2 Simpson框图(引用柯以佩编《大学化学实验》)
2.2 Simpson 框图(引用柯以侃编《大学化学实验》)
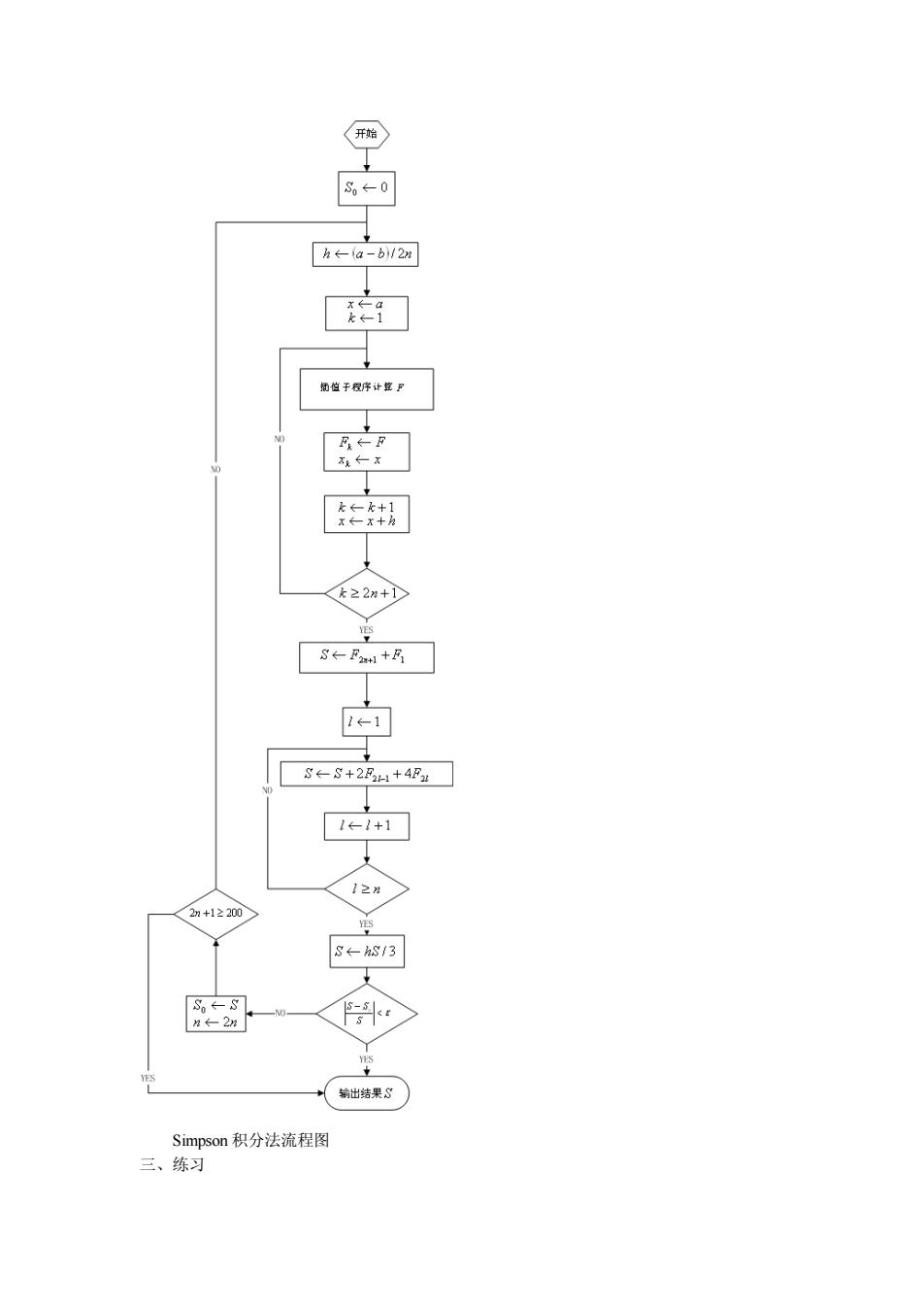
2n+12200 Simpson积分法流程 三、练习
Simpson 积分法流程图 三、练习
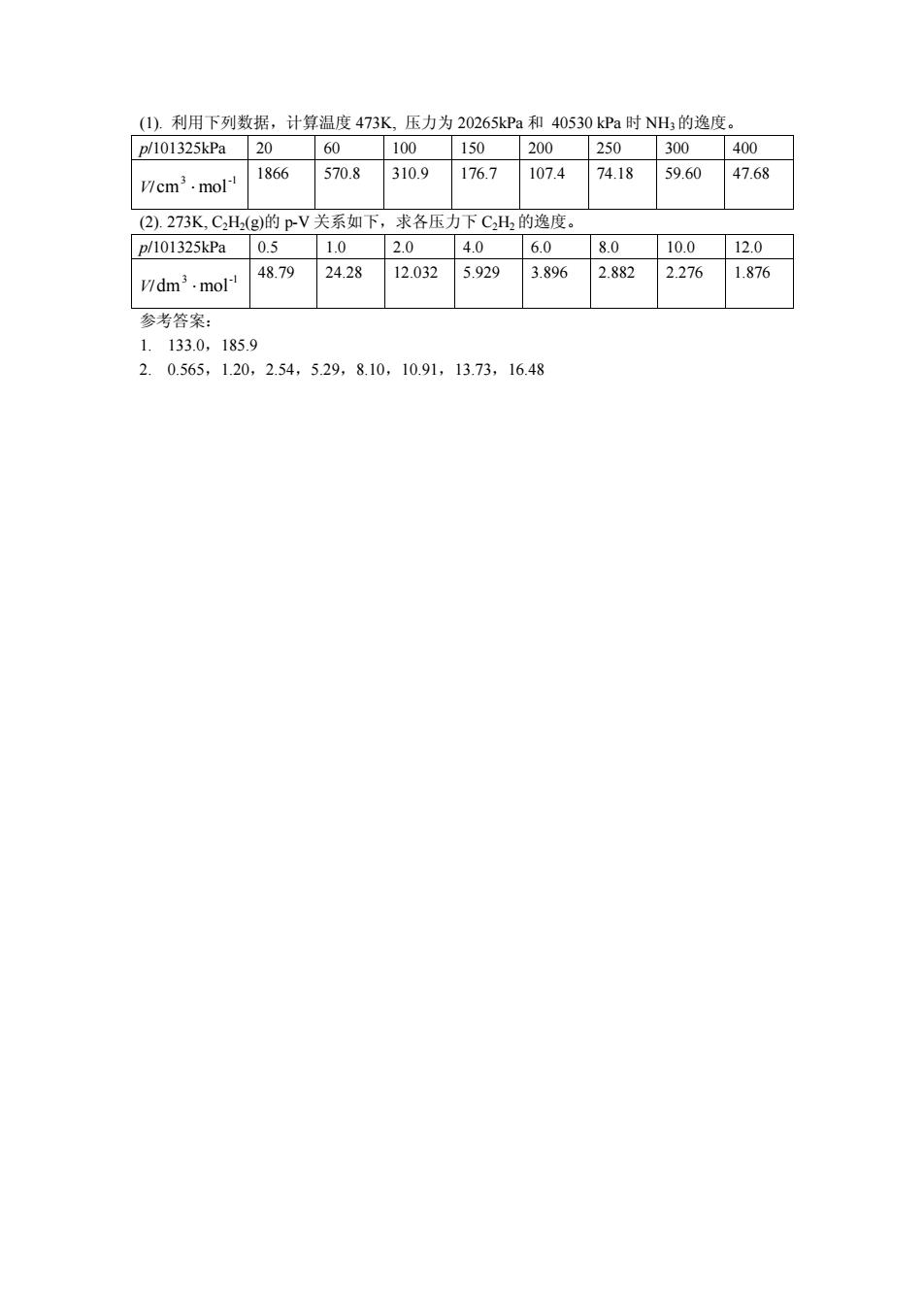
(1).利用下列数据,计算温度473K,压力为20265kPa和40530kPa时NH3的逸度。 p/101325kPa 20 60 100 150 200 250 300 400 1866 570.8 310.9 176.7 107.4 74.18 59.60 47.68 V/cm3.mol- (2).273K,CH2(g)的p-V关系如下,求各压力下C2H2的逸度。 p/101325kPa 0.5 1.0 2.0 4.0 6.0 8.0 10.0 12.0 48.79 24.28 12.032 5.929 3.896 2.882 1.876 V/dm3.mol 2.276 参考答案: 1.133.0,185.9 2.0.565,1.20,2.54,5.29,8.10,10.91,13.73,16.48
(1). 利用下列数据,计算温度 473K, 压力为 20265kPa 和 40530 kPa 时 NH3的逸度。 p/101325kPa 20 60 100 150 200 250 300 400 V/ 3 -1 cm ×mol 1866 570.8 310.9 176.7 107.4 74.18 59.60 47.68 (2). 273K, C2H2(g)的 p-V 关系如下,求各压力下 C2H2的逸度。 p/101325kPa 0.5 1.0 2.0 4.0 6.0 8.0 10.0 12.0 V/ 3 -1 dm ×mol 48.79 24.28 12.032 5.929 3.896 2.882 2.276 1.876 参考答案: 1. 133.0,185.9 2. 0.565,1.20,2.54,5.29,8.10,10.91,13.73,16.48