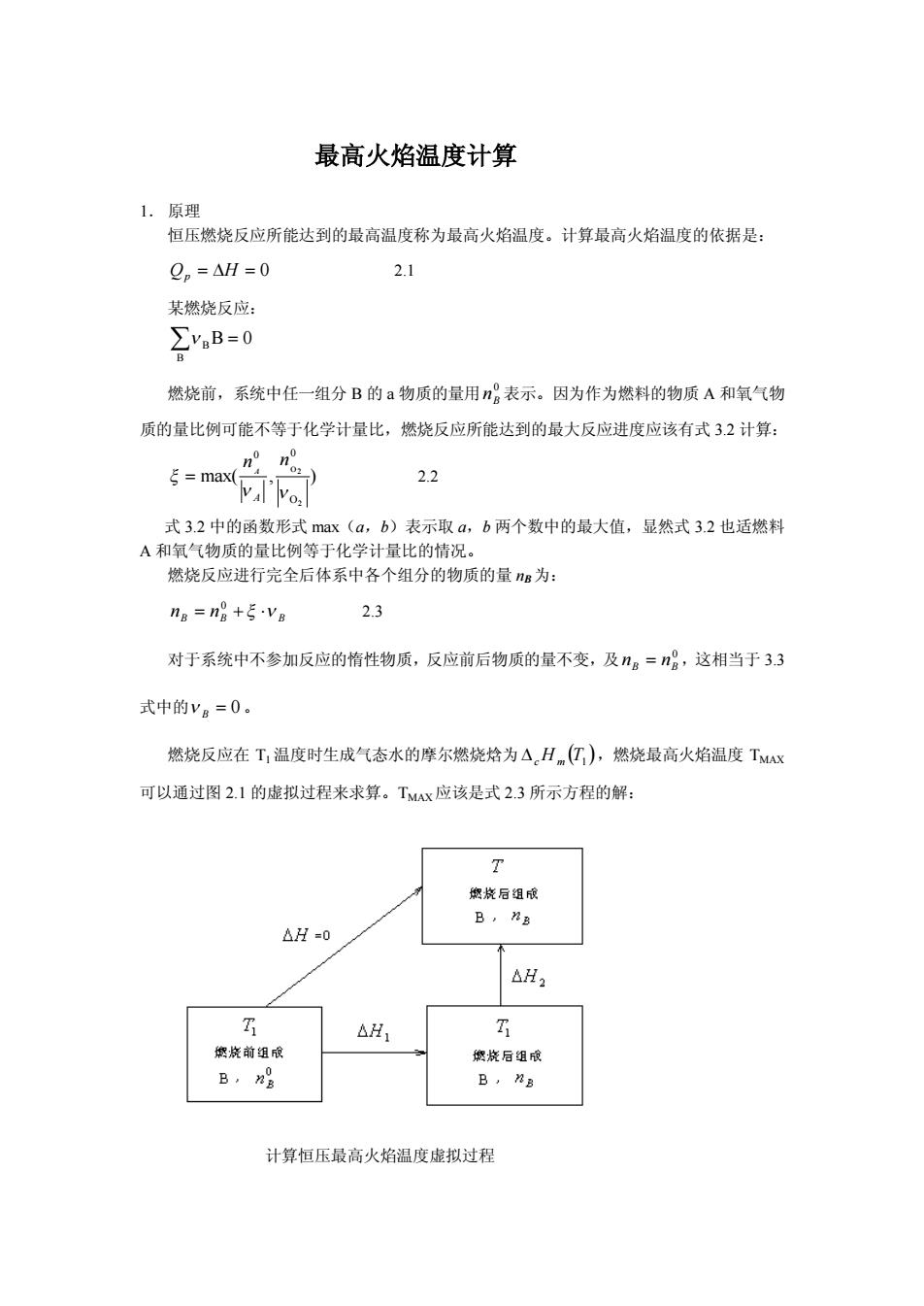
最高火焰温度计算 1,原理 恒压燃烧反应所能达到的最高温度称为最高火焰温度。计算最高火焰温度的依据是: p=AH=0 2.1 某燃烧反应: ∑,B=0 燃烧前,系统中任一组分B的a物质的量用n表示。因为作为燃料的物质A和氧气物 质的量比例可能不等于化学计量比,燃烧反应所能达到的最大反应进度应该有式32计算: V'Vo 2.2 式32中的函数形式max(a,b)表示取a,b两个数中的最大值,显然式32也适燃料 A和氧气物质的量比例等于化学计量比的情况。 燃烧反应进行完全后体系中各个组分的物质的量s为: ng=ng+va 2.3 对于系统中不参加反应的惰性物质,反应前后物质的量不变,及n。-n,这相当于33 式中的yg=0。 燃烧反应在T,温度时生成气态水的摩尔燃烧焓为△。H(亿),燃烧最高火焰温度TM 可以通过图2.1的虚拟过程米求算。Tx应该是式2.3所示方程的解: T 您烧后组成 B.B △H=0 △H2 △H1 烧前组成 搬烧后组成 B, B.Mg 计算恒压最高火焰温度虚拟过程
最高火焰温度计算 1. 原理 恒压燃烧反应所能达到的最高温度称为最高火焰温度。计算最高火焰温度的依据是: Qp = DH = 0 2.1 某燃烧反应: å = B B n B 0 燃烧前,系统中任一组分 B 的 a 物质的量用 0 B n 表示。因为作为燃料的物质 A 和氧气物 质的量比例可能不等于化学计量比,燃烧反应所能达到的最大反应进度应该有式 3.2 计算: max( , ) 2 O2 O 0 0 n n x n n A A = 2.2 式 3.2 中的函数形式 max(a,b)表示取 a,b 两个数中的最大值,显然式 3.2 也适燃料 A 和氧气物质的量比例等于化学计量比的情况。 燃烧反应进行完全后体系中各个组分的物质的量 nB为: B B B n = n + x ×n 0 2.3 对于系统中不参加反应的惰性物质,反应前后物质的量不变,及 0 B B n = n ,这相当于 3.3 式中的 = 0 n B 。 燃烧反应在 T1 温度时生成气态水的摩尔燃烧焓为 ( ) DcHm T1 ,燃烧最高火焰温度 TMAX 可以通过图 2.1 的虚拟过程来求算。TMAX应该是式 2.3 所示方程的解: 计算恒压最高火焰温度虚拟过程

△H=△H,+H, =A,H)+∑aCpmadT 0 2.3 将式21代入3.3式,得: s.)+aa-TH∑6,×10--T写zn410-6-7刊 dxn-》-0 24 用Newton-Raphson迭代法解出T即最高火焰温度TMax。 Newton-Raphson迭代法的函数f(x)为3.1式等号左边,f'(x)为: ∑"0,+2n6,×10-7+∑"a×10*T +∑4,×10 2.5 从手册中可以查到298K下物质的标准摩尔生成焓或标准摩尔燃烧焓可以计算该温度下 的焓变△H,。因为燃烧温度很高,水为气态,应该用气态水的数据计算。通过解方程3.1 得到最高火焰温度T2 2.程序流程图
DH = DH1 + DH2 = ( ) å ò D + T T Hm T n Cp m dT 1 , ,B B x c 1 B =0 2.3 将式 2.1 代入 3.3 式,得: ( ) ( ) ( ) ( ) 0 1 1 10 10 3 1 10 2 1 1 5 3 1 2 6 3 1 3 2 B 1 B B 1 = ÷ ÷ ø ö ç ç è æ - ´ - D + - + ´ - + ´ - å å å å - - T T n d H T n a T T n b T T n c T T B B B B B m B B B B x …………..2.4 用 Newton-Raphson 迭代法解出 T 即最高火焰温度 TMAX。 Newton-Raphson 迭代法的函数 f (x) 为 3.1 式等号左边, ( ) / f x 为: ; 1 10 10 10 2 5 3 6 2 å å å å + ´ + ´ + ´ - - B B B B B B B B B B B B T n d n a n b T n c T ………………2.5 从手册中可以查到 298K 下物质的标准摩尔生成焓或标准摩尔燃烧焓可以计算该温度下 的焓变 DH1 。因为燃烧温度很高,水为气态,应该用气态水的数据计算。通过解方程 3.1 得到最高火焰温度 T2。 2.程序流程图

开始 计算: 反应进度56.2式) 读入: 燃烧前系统中物种 锡簧量气禁守名 物质的量材。 燃烧反应式中各组 计量系数VB 信性物质:V=0 餐 读入最大达代次数:I 允许误差:& 读入:T,△HT 结束 最高火焰温度计算程序流程图 3.练习 (1)水蒸气在298K下的标准生成摩尔生成格为-241.818kmo,求1体积H2(g)在0.5 体积的02中在10OPa,初始温度298K的条件下燃烧时所能达到的恒压最高火焰温度。 ②C0(g)与C0,的298x下的标准摩尔生成格数据分别为-10525Jm0和393509 kmor,求1体积C0(g)在10体积的空气中在100kPa,初始温度298K的条件下燃烧时 所能达到的恒压最高火焰温度。(1体积空气设由0.21体积氧气和0.79体积氮气组成) 参考答案:1.4845K2.1158K Cpm(H2)/Jmol.K1=26.88+4.347×10-3.T1K-0.3265×106.T2/K2 Cpn(0)/J.mol'.K=28.17+6.297×10-3.T/K-0.7494×10-6.T21K Cp(日,0,g)/Jmol.K=29.16+14.49×10-3.T/K-2.022×106.T21K2 Cpm(C0,g/Jmol.K=26.37+7.6831×10-3.T/K-1.172×10-6.T2/K2 Cp(C02,g/Jmol.K--26.75+42.258×10-3.T/K-14.25×106.T21K2 Cmn(N2)/Jmol.K=27.32+6.226×10-3.T1K-0.9502×106.T2/K2 PDF文件使用“pdfFactory Pro”试用版本创建,fineprint,con,cn
最高火焰温度计算程序流程图 3. 练习 (1) 水蒸气在 298K 下的标准生成摩尔生成焓为-241.818 kJ·mol-1,求 1 体积 H2(g)在 0.5 体积的 O2中在 100kPa,初始温度 298K 的条件下燃烧时所能达到的恒压最高火焰温度。 (2) CO(g)与 CO2 的 298K 下的标准摩尔生成焓数据分别为-110.525 kJ·mol-1 和-393.509 kJ·mol-1,求 1 体积 CO(g)在 10 体积的空气中在 100kPa,初始温度 298K 的条件下燃烧时 所能达到的恒压最高火焰温度。(1 体积空气设由 0.21 体积氧气和 0.79 体积氮气组成) 参考答案:1. 4845K 2. 1158K ( ) -1 -1 3 6 2 2 Cp,m H2 /J×mol × K = 26.88 + 4.347 ´10 ×T / K - 0.3265´10 ×T / K - - ( ) -1 -1 3 6 2 2 Cp,m O2 /J× mol × K = 28.17 + 6.297 ´10 ×T / K - 0.7494´10 ×T / K - - ( ) -1 -1 3 6 2 2 Cp,m H2O,g /J×mol × K = 29.16 +14.49´10 ×T / K - 2.022´10 ×T / K - - ( ) -1 -1 3 6 2 2 Cp,m CO, g /J×mol × K = 26.37 + 7.6831´10 ×T / K -1.172´10 ×T / K - - ( ) -1 -1 3 6 2 2 Cp,m CO2 ,g /J×mol × K = 26.75 + 42.258´10 ×T / K -14.25´10 ×T / K - - ( ) -1 -1 3 6 2 2 Cp,m N2 /J×mol × K = 27.32 + 6.226´10 ×T / K - 0.9502 ´10 ×T / K - - PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.com.cn