
第6节 第七章 微分法在儿何上的五用 一、 空间曲线的切线与法平面 二、曲面的切平面与法线 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 一、空间曲线的切线与法平面 第6节 二、曲面的切平面与法线 微分法在几何上的应用 第七章
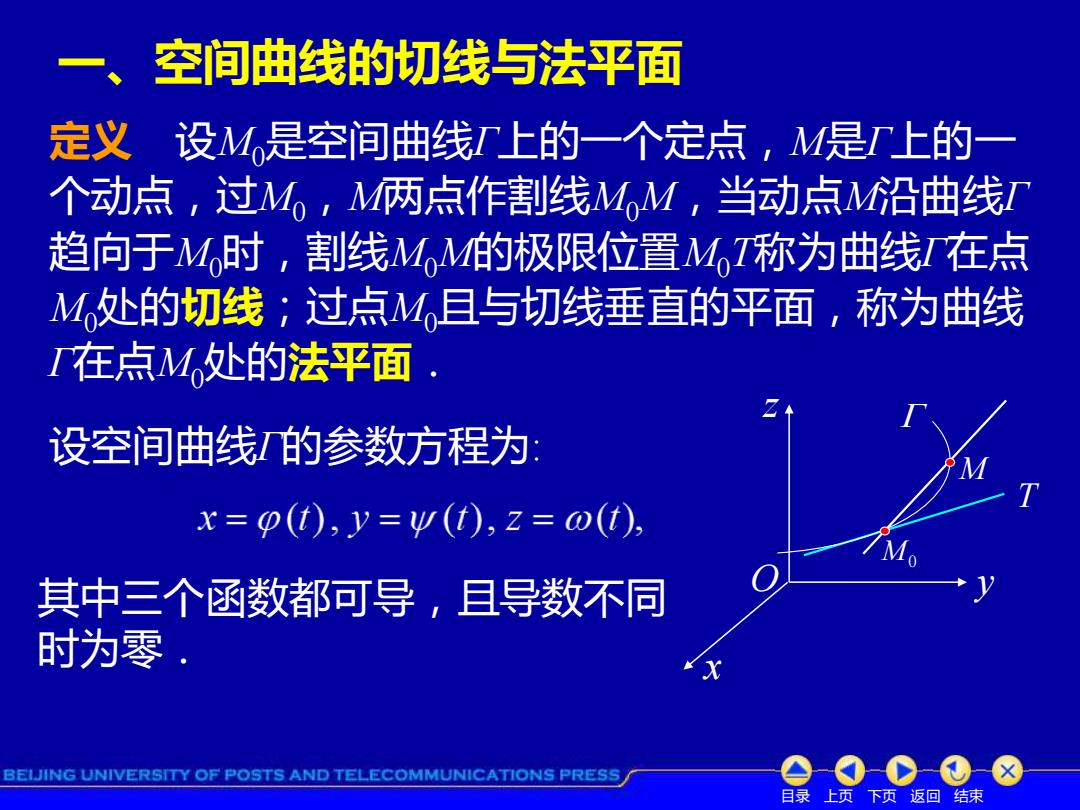
一、空间曲线的切线与法平面 定义设M,是空间曲线T上的一个定点,M是上的 个动点,过M,,M两点作割线MM,当动点M沿曲线IT 趋向于M时,割线MoM的极限位置M,I称为曲线I在点 M处的切线;过点M,且与切线垂直的平面,称为曲线 I在点M处的法平面 设空间曲线的参数方程为 x=g(t),y=w(t),z=@(t). 其中三个函数都可导,且导数不同 时为零 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 一、空间曲线的切线与法平面 定义 设M0是空间曲线Γ上的一个定点,M是Γ上的一 个动点,过M0,M两点作割线M0M,当动点M沿曲线Γ 趋向于M0时,割线M0M的极限位置M0T称为曲线Γ在点 M0处的切线;过点M0且与切线垂直的平面,称为曲线 Γ在点M0处的法平面. 设空间曲线Γ的参数方程为: 其中三个函数都可导,且导数不同 时为零. T M0 M x y z O

设T上的点M(x,,。)对应t=to,参数1=t对应曲 T上定点M(x,o,),参数t=t+△对应曲线T上动 点Mx+△x,+△,二+△),则割线MM的方程是 X-X=y-y%-2-0 △x △y △z 切线方程 X-0= y-y0-2-20 p'(o)V(o)⑩'(to) 法平面方程 0'(to(x-xo)+w()(y-y%)+w'(t02-20)=0 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 0 0 0 x x y y z − z = − = − ( ) 0 t ( ) 0 t ( ) 0 t ( , , ) , 0 0 0 0 0 设上的点M x y z 对应t = t Γ上定点M0 (x0,y0,z0 ),参数t=t 0+Δt对应曲线Γ上动 点M(x0+Δx,y0+Δy,z0+Δz),则割线M0M的方程是 ( )( ) 0 0 t x − x ( )( ) 0 0 + t y − y +(t0 )(z − z0 ) = 0 法平面方程 切线方程 T M0 M x y z O . 0 0 0 z z z y y y x x x − = − = − 参数t=t 0对应曲

例7.6.2求曲线x=1,y=t2,z=t3在点(1,1,1)处的切线 及法平面方程 解:x=1,y=21,z=32,点(1,1,1)对应于t=1, 故切向量为T=(1,2,3) 思考:光滑曲线 因此所求切线方程为 r:[y=0(x) x-1y-1- z=w(x) 2-1 2 3 的切向量有何特点? 法平面方程为 X=X 答: T:y=0(x) (x-1)+2(y-1)+3(2-1)=0 z=v(x) 即 x+2y+3z=6 切向量T=(1,0,w) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例7.6.2 求曲线 2 3 x = t, y = t , z = t 在点 (1, 1, 1) 处的切线 及法平面方程. 1, 2 , 3 , 2 解: x = y = t z = t 点(1, 1, 1) 对应于 故切向量为 T = (1, 2, 3) 因此所求切线方程为 1 1 −1 = − = x − y z 1 2 3 法平面方程为 (x −1)+ 2 ( y −1) + 3(z −1) = 0 即 x + 2y + 3z = 6 = = ( ) ( ) : z x y x 思考: 光滑曲线 的切向量有何特点? T = (1, ,) 答: = = = ( ) : ( ) z x y x x x 切向量

二、曲面的切平面与法线 设有光滑曲面:F(x,y,z)=0 通过其上定点M(x,,任意引一 条光滑曲线 T:x=p(),y=V(),z=0(t),设t=t0对应点Mo,且 p(to),y(to),0'(to不全为0.则T在 点M的切向量为 T=(0'(to),y(to),0'(o) 切线方程为 X-0-y-y0-2-20 p'(to)v'(to) @'(to) 下面证明:∑上过点M,的任何曲线在该点的切线都 在同一平面上.此平面称为∑在该点的切平面 BELJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 二、曲面的切平面与法线 设 有光滑曲面 通过其上定点 0 设 t = t 对应点 M0 , 切线方程为 ( ) ( ) ( ) 0 0 0 0 0 0 t z z t y y t x x − = − = − 不全为0 . 则 在 且 点 M 0的切向量为 任意引一条光滑曲线 下面证明: 此平面称为 在该点的切平面. 上过点 M 0的任何曲线在该点的切线都 在同一平面上. ( ( ), ( ), ( )) 0 0 0 T = t t t M0 T

证:T:x=p(t),y=w(),z=0(t)在∑上 F(p(t),w(t),o(t)≡0 两边在t=t0处求导,注意t=t,对应点M 得 Fx(x0,J0,20)0'(o)+Fy(x0,0,20)w'(0) +F(x0,y0,20)o'(to)=0 令T=(p'(),y(o),⑩'(o)》 7=(Fx(x0,y0,20),Fy(x0,0,20),F(x0,0,20) 切向量T⊥ 由于曲线T的任意性,表明这些切线都在以n为法向量 的平面上,从而切平面存在 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 M0 T 证: 在 上, F( (t), (t), (t)) 0 , 两边在 t = t0 处求导 , 0 M0 注意t = t 对应点 ( ) 0 t = 0 ( , , ) 0 0 0 F x y z x ( , , ) 0 0 0 F x y z + y ( , , ) 0 0 0 F x y z + z ( ) 0 t ( ) 0 得 t ( ( ), ( ), ( )) 0 0 0 T = t t t ( ( , , ), ( , , ), ( , , )) 0 0 0 0 0 0 0 0 0 n F x y z F x y z F x y z = x y z 令 切向量 T ⊥ n 由于曲线 的任意性 , 表明这些切线都在以 为法向量 的平面上 , 从而切平面存在

曲面∑在点M,的法向量: n=(x(x0,0,20),Fy(x0,0,20),F(x0,0,20》 切平面方程 Fx(x0,0,20)(x-xo)+F,(x0,0,20)(y-0) +F2(x0,y0,20)2-20)=0 过M,点且垂直于切平面的直线 称为曲面∑在点M,的法线. 法线方程 x-x0 y-Yo 2-20 F(x0,0,20)F,(x0,y0,20) F2(x0,Jy0,20) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 ( , , )( ) 0 0 0 0 F x y z x x x − 曲面 在点 M0 的法向量: 法线方程 0 0 0 x x y y z − z = − = − ( , , )( ) 0 0 0 0 F x y z y y + y − ( , , )( ) 0 + Fz x0 y0 z0 z − z0 = 切平面方程 ( , , ) 0 0 0 F x y z x ( , , ) 0 0 0 F x y z y ( , , ) 0 0 0 F x y z z ( ( , , ), ( , , ), ( , , )) 0 0 0 0 0 0 0 0 0 n F x y z F x y z F x y z = x y z 过M0点且垂直于切平面的直线 称为曲面 在点 M0 的法线. M0 T

例7.6.5 求球面x2+y2+:2=14在点(1,2,3)处的切 平面及法线方程 解:令 F(x,y,2)=x2+y2+z2-14 法向量 n=(2x,2y,22) n1,2.3)=(2,4,6) 所以球面在点(1,2,3)处有 切平面方程 2(x-1)+4(y-2)+6(z-3)=0 即 x+2y+3z-14=0 法线方程 x-1_y-22-3 2 3 X 即 y (可见法线经过原点,即球心) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例7.6.5 求球面 14 2 2 2 x + y + z = 在点(1 , 2 , 3) 处的切 平面及法线方程. 解: 令 所以球面在点 (1 , 2 , 3) 处有: 切平面方程 2(x −1) 即 法线方程 1 2 −3 = − = x − y z + 4( y − 2) + 6(z − 3) = 0 1 2 3 法向量 n = (2 x, 2 y, 2 z) (2, 4, 6) (1, 2,3) n = 即 1 2 3 x y z = = (可见法线经过原点,即球心)

内容小结 1.空间曲线的切线与法平面 x=p(t) 空间光滑曲线 r:y=w(t) z=@(t) 切向量 7=(p'(t),W'(to),0'(to)》 切线方程 x-x0y-y0 2-20 @'(to) 法平面方程 p(to)(x-xo)+W(to)(y-o)+0'()a-o)=0 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 1. 空间曲线的切线与法平面 切线方程 0 0 0 x x y y z − z = − = − 法平面方程 ( )( ) 0 0 t x − x = = = ( ) ( ) ( ) : z t y t x t 空间光滑曲线 切向量 内容小结 ( ) 0 t ( ) 0 t ( ) 0 t ( )( ) 0 0 + t y − y +(t0 )(z − z0 ) = 0 ( ( ), ( ), ( )) 0 0 0 T = t t t

2.曲面的切平面与法线 空间光滑曲面Σ:F(x,y,z)=0 曲面∑在点M(x,yo,2o)的法向量 n=(F(x0,0,20),F,(x0,0,20),F(x0,y0,20》 切平面方程 Fx(x0,y0,20)(x-x0)+Fy(x0,0,20)(y-y0) +F(x0,y0,20)(2-20)=0 法线方程 x-x0 y-Yo 2-20 Fx(x0,y0,20) F,(x0,0,20)F(x0,y%,20) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 空间光滑曲面 曲面 在点 法线方程 ( , , ) 0 0 0 0 F x y z x x x − ( , , ) 0 0 0 0 F x y z y y y − = ( , , ) 0 0 0 0 F x y z z z z − = ( , , )( ) ( , , )( ) 0 0 0 0 0 0 0 0 F x y z x x F x y z y y x − + y − 的法向量 + Fz (x0 , y0 ,z0 )(z − z0 ) = 0 切平面方程 2. 曲面的切平面与法线 ( ( , , ), ( , , ), ( , , )) 0 0 0 0 0 0 0 0 0 n F x y z F x y z F x y z = x y z