
第1节 第七章 多无品数的基存橇念写极限 平面区域的概念 二、 多元函数的概念 三、二元函数的极限与连续性 四、有界闭区域上多元连续函数的性质 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 第 第七章 1节 一、平面区域的概念 二、多元函数的概念 三、二元函数的极限与连续性 四、有界闭区域上多元连续函数的性质 多元函数的基本概念与极限

一、平面区域的概念 1.平面点集 二维平面2上具有某种性质的点的集合,称为平面 点集,记作 E=《x,y)川(x,y)具有的性质 例如,在R2上以坐标原点O0,0)为中心,为半径的圆 内所有点P(x,y)的集合为 C={(x,y川x+y2<r2或记成C={PlOPKr BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 一、平面区域的概念 1.平面点集 二维平面R2上具有某种性质的点的集合,称为平面 点集,记作 例如,在R2上以坐标原点O(0,0)为中心,r为半径的圆 内所有点P(x,y)的集合为 ( , )| || | . 2 2 2 C = x y x + y r 或记成 C = P OP r E = (x, y )|(x, y)具有的性质

2.邻域 点集U(P,ò)={PPP<δ,称为点P的δ邻域. 例如,在平面上, U(B,)={《x,y)V(x-)2+(y-%)2<δ}(圆邻域) 在空间中, U(B,8)={《x,y,2)V(x-x)2+0y-o)2+(2-2)2<ò} (球邻域 说明:若不需要强调邻域半径δ,也可写成U(P) 点P的去心邻域记为U(P)={P0<PP<δ} BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS -N 目录上页下页返回结束
目录 上页 下页 返回 结束 PP δ 0 0 2. 邻域 点集 称为点 P0 的 邻域. 例如,在平面上, U(P0 , δ ) = (x, y) (圆邻域) 在空间中, U(P0 , ) = (x, y,z) (球邻域) 说明:若不需要强调邻域半径 ,也可写成 ( ). U P0 点 P0 的去心邻域记为 PP δ 0

在讨论实际问题中也常使用方邻域,因为方邻域与圆 邻域可以互相包含 °0 平面上的方邻域为 U(,δ)={(x,y)x-xo<ò,ly-yo<ò} BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 在讨论实际问题中也常使用方邻域, 平面上的方邻域为 U(P0 ,δ ) = (x, y) 。 P0 因为方邻域与圆 邻域可以互相包含

3.区域 1)内点、外点、边界点 设有点集E及一点P: ● 若存在点P的某邻域乙UP)cE, 则称P为E的内点: 若存在点P的某邻域U(P)∩E=⑦ 则称P为E的外点 ·若对点P的任一邻域乙UP)既含E中的内点也含E 的外点,则称P为E的边界点 显然E的内点必属于E,E的外点必不属于E,E的 边界点可能属于E,也可能不属于E BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS -OC 目录上页下页返回结束
目录 上页 下页 返回 结束 3. 区域 1) 内点、外点、边界点 设有点集 E 及一点 P : • 若存在点 P 的某邻域 U(P) E , • 若存在点 P 的某邻域 U(P)∩ E = , • 若对点 P 的任一邻域 U(P) 既含 E中的内点也含 E E 则称 P 为 E 的内点; 则称 P 为 E 的外点 ; 的外点 , 则称 P 为 E 的边界点 . 显然, E 的内点必属于 E , E 的外点必不属于 E , E 的 边界点可能属于 E, 也可能不属于 E . P

2)聚点 若对任意给定的δ,点P的去心 邻域U(P,δ)内总有E中的点,则 称P是E的聚点 聚点可以属于E,也可以不属于E(因为聚点可以为 E的边界点) 所有聚点所成的点集成为E的导集 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 2) 聚点 若对任意给定的 , 点P 的去心 E 邻域 内总有E 中的点 , 则 称 P 是 E 的聚点. 聚点可以属于 E , 也可以不属于 E (因为聚点可以为 所有聚点所成的点集成为 E 的导集 . E 的边界点 )

3)开区域及闭区域 若点集E的点都是内点,则称E为开集; ·E的边界点的全体称为E的边界,记作∂E; 若点集E一E,则称E为闭集; 若集E中任意两点都可用一完全属于E的折线相连 则称E是连通的; 连通的开集称为开区域,简称区域; 开区域连同它的边界一起称为闭区域 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 E 3) 开区域及闭区域 • 若点集 E 的点都是内点,则称 E 为开集; • 若点集 E E , 则称 E 为闭集; • 若集 E 中任意两点都可用一完全属于 E 的折线相连 , • 开区域连同它的边界一起称为闭区域. 则称 E 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; 。 。 • E 的边界点的全体称为 E 的边界, 记作E ;
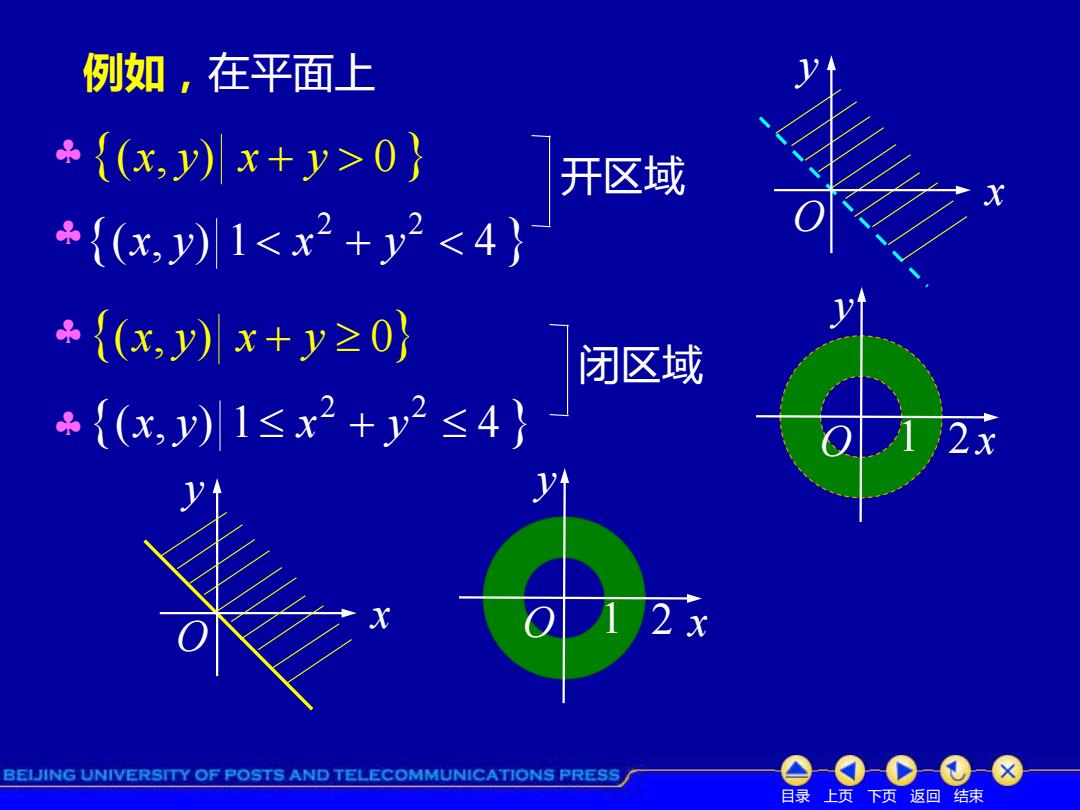
例如,在平面上 ÷{(x,y)x+y>0} 开区域 {(x,y)1<x2+y2<4} ÷{(x,y)x+y≥0} 闭区域 ÷{(x,y)1≤x2+y2≤4》 2x 2 x BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例如,在平面上 (x, y) x + y 0 ( , ) 1 4 2 2 x y x + y (x, y) x + y 0 ( , ) 1 4 2 2 x y x + y 开区域 闭区域 x y O x y O 1 2 x y O x y O 1 2

整个平面是最大的开域 也是最大的闭域 点集{(x,y)x>1}是开集 但非区域 对点集E,若存在正数K,使一切点P∈E与坐标原点 O的距离OP飞K,则称E为有界集,否则称为无 界集。 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 整个平面 点集 (x, y) x 1 是开集, 是最大的开域 , 也是最大的闭域 ; 但非区域 . −1 1 • 对点集 E , 若存在正数 K , 使一切点 PE 与坐标原点 O 的距离 OP K , 则称 E 为有界集 , 界集. 否则称为无 x y O

4.n维空间 n元有序数组(,x2,…,xn)的全体所构成的集合记作 R",即R=R×Rx…×R {(,x2,…,xnxk∈R,k=1,2,…,n} R”中的每一个元素用单个粗体字母x表示,即 x=(x1,x2,…,xn) 任给x=(x,x,,xn)y=(,y2,,yn)∈R”,九∈R 定义:x+y=(x1+,x2+2,…,xn+yn) 线性运算 九x=(见x,人2,…,九xn) 定义了线性运算的R"称为n维空间,其元素称为点或 n 维向量x,称为x的第i个坐标或第i个分量 零元0=(0,0,,0)称为R”中的坐标原点或零向量 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 4. n 维空间 n 元有序数组 的全体所构成的集合记作 , n R 即 R = R R R n R n 中的每一个元素用单个粗体字母 x 表示, 即 n 定义了线性运算的R 定义: ( , , , ) 1 2 n x = x x x ( , , , ) 1 1 2 2 n n x + y = x + y x + y x + y 线性运算 其元素称为点或 n 维向量. xi 称为 x 的第 i 个坐标 或 第 i 个分量. 称为 n 维空间