
第2节 第十章 常款项级款的审敛法 正项级数及其审敛法 二、交错级数及其审敛法 三、绝对收敛与条件收敛 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 二、交错级数及其审敛法 三、绝对收敛与条件收敛 第2节 一、正项级数及其审敛法 常数项级数的审敛法 第十章

一、正项级数及其审敛法 00 若4n≥0,则称∑4n 为正项级数 n=l 定理1正项级数∑4n收敛 二部分和数列{} n=l (n=1,2,…)有界 证:“→”若∑4n收敛,则{s}收敛故有界 n=1 一”un≥0,.部分和数列{sn}单调递增 又已知{s,}有界故{s,}收敛,从而∑4n也收敛 n=1 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 一、正项级数及其审敛法 若 0, un n=1 un 定理 1 正项级数 收敛 部分和数列 有界. 若 收敛 , ∴部分和数列 又已知 有界, 故 从而 故有界. 则称 为正项级数. 单调递增, 收敛 , 也收敛. 证: “ ” “ ” 则 收敛

定理2(比较审敛法) 设∑n∑n 都是正项级数, 且un≤Vn(n=1,2,…) (1)如果级数∑y,收敛,则级数∑4n也收敛: n=1 (2)如果级数 ∑4发散,则级数∑y,也发散 n=1 n=1 证:(1)由定理1可知,当级数∑y收敛时,其部分和 数列必有界,于是有心0,使得 0s∑y≤M BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 定理2 (比较审敛法) 设 且 (1) 如果级数 则级数 (2) 如果级数 则级数 收敛 , 也收敛 ; 发散 , 也发散. 都是正项级数, (n=1,2,…) . 证:(1)由定理1可知,当级数 收敛时,其部分和 数列必有界,于是有M>0,使得

又4n≤n(n=1,2,…),故 0s∑4,≤∑≤M, 因而级数∑4的部分和数列有界,级数∑收敛. m=1 n=1 2)若级数∑4,发散则级数立y,必发散. =1 n=] BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 又un≤vn (n=1,2,…),故 因而级数 的部分和数列有界,级数 收敛. (2) 若级数 发散, 则级数 必发散.

准论设∑4∑ 都是正项级数,并且4n≤wm 0 (0,n2N,N为某一自然数). (1)如果级数 ∑收敛,则级数∑ 4n也收敛; n=1 n=1 (2)如果级数∑4,发散,则级数∑yn也发散. n=1 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 推论 设 (1) 如果级数 则级数 (2) 如果级数 则级数 收敛 , 也收敛 ; 发散 , 也发散 . 都是正项级数,并且un≤kvn ( k>0,n≥N,N为某一自然数 )

例10.2.3 讨论级数++…+ 的敛散性,其中常数p>0. 解:当p≤1,因为对一切n∈N+, n 又调和级数 发激,由比纹审敛法可知P级数。 n= 发散. BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例10.2.3 讨论 p -级数 1 1 1 1 1 234 p p p p n + + + + + + 的敛散性,其中常数 p > 0. 解: 当 p 1, 因为对一切 又调和级数 =1 1 n n 由比较审敛法可知 p 级数 n 1 发散 . 发散
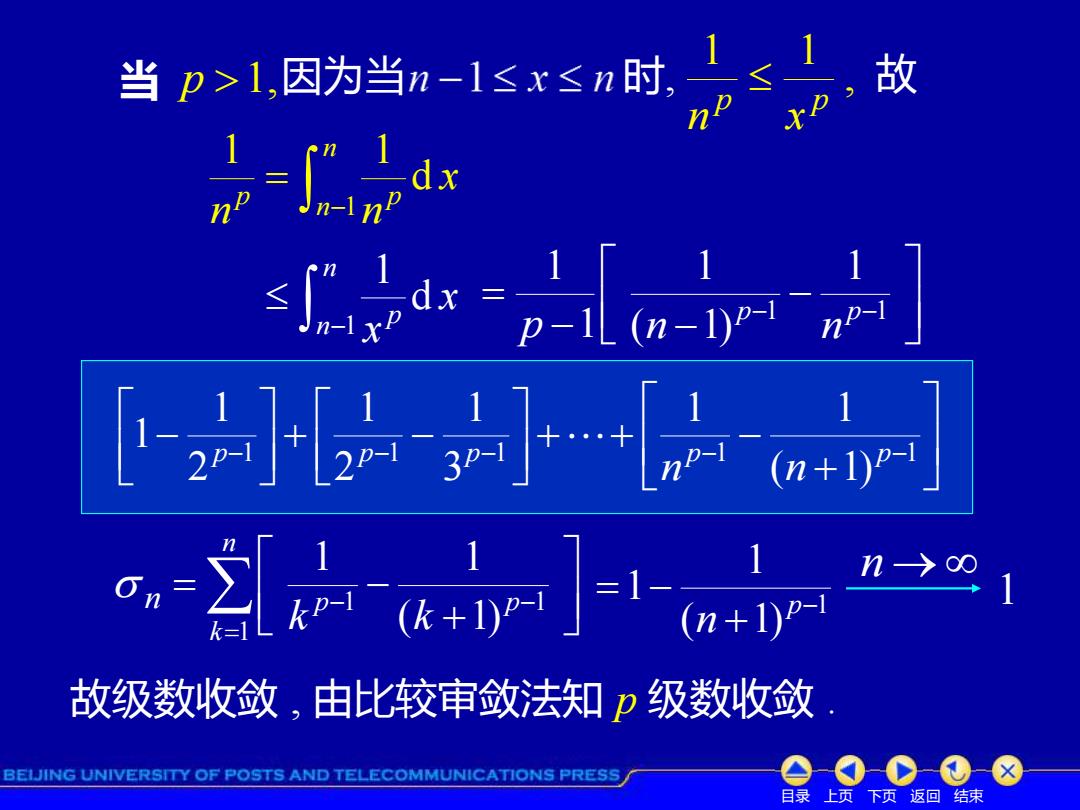
当p>1,因为当n-1≤x≤n时 , 故 dx [-][ 故级数收敛,由比较审敛法知p级数收敛 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 p 1, 因为当 , 1 1 p p n x 故 − = n n p p x n 1 n d 1 1 − n n p x 1 x d 1 − − − = −1 −1 1 ( 1) 1 1 1 p p p n n 考虑强级数 − − − − = 1 1 2 1 ( 1) 1 p p n n n 的部分和 n + − = − − = 1 1 1 ( 1) 1 1 p p n k k k n → 故级数收敛 , 由比较审敛法知 p 级数收敛 . 时, 1 ( 1) 1 1 − + = − p n 1 当 + + + − + − − −1 −1 −1 −1 −1 ( 1) 1 1 3 1 2 1 2 1 1 p p p p p n n

例10.2.4判定级数 的敛散性 解:因为 3= √n(n+in+ly (n=1,2,…) 而级数 发散 k=2 根据比较审敛法可知,所给级数发散 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 判定级数 的敛散性. 解: 因为 2 ( 1) 1 ( 1) 1 + n n + n 而级数 = = 2 1 k k 发散 根据比较审敛法可知, 所给级数发散 . 例10.2.4

定理3(比较审敛法的极限形式) 设两正项级数 00 ∑4n,∑Yn满足lim4n=1,则有 n=1 7n=1 n→oVn (1)当0≤1N时, 42<1+1,即un<(0+y BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 定理3 (比较审敛法的极限形式) lim l, v u n n n = → 则有 (2) 当 l = +∞ 证: (1)由极限定义,对 设两正项级数 满足 (1) 当 0 ≤ l < +∞

00 而级数Σ'收敛,根据比较审敛法的推论,知级数 n=1 ∑4,收敛 n= (2)按已知条件 im”存在,如果级数∑u,收敛,则 n->Un n=1 由结论(1)必有∑yn收敛,但已知级数∑yn发散, 因此级数∑u,不可能收敛,即级数∑4n发散· n= BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 而级数 收敛,根据比较审敛法的推论,知级数 收敛. (2)按已知条件 存在,如果级数 收敛,则 由结论(1)必有 收敛,但已知级数 发散, 因此级数 不可能收敛,即级数 发散.