第6节 第三章 孤微分与曲幸 曲线的弯 〔与切线的转角有关 曲程度 与曲线的弧长有关 M 主要内容: 一、弧微分 二、曲率及其计算 三、曲率圆 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 自录上页 下负返回 结束
目录 上页 下页 返回 结束 第6节 曲线的弯 曲程度 与切线的转角有关 与曲线的弧长有关 主要内容: 一、 弧微分 二、 曲率及其计算 三、 曲率圆 M M M 弧微分与曲率 第三章
一、 弧微分 设y=f(x)在(a,b)内有连续导数,其图形为AB 弧长s=AM=s(x) y=f(x) M △S MM'MM' △X MM' △x MM'V(△x)2+(△y)2 MM' △x x+△X MM' =生 MM lim ±1 △x0 MM' :s)=limA=1+yW △x>0△X BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 录 上 返回 结束
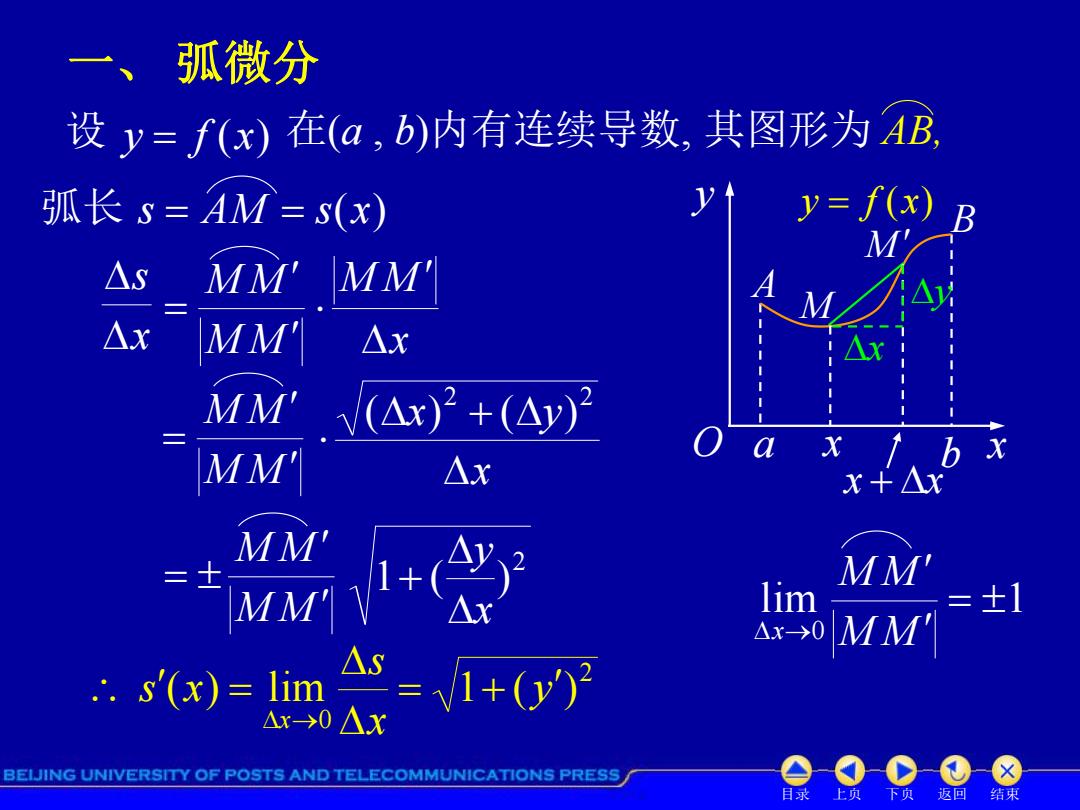
目录 上页 下页 返回 结束 一、 弧微分 设 y f (x) 在(a , b)内有连续导数, 其图形为 AB, 弧长 s AM s(x) x s M M M M x M M M M M M x x y 2 2 ( ) ( ) M M M M 2 1 ( ) x y x s s x x 0 ( ) lim 2 1 ( y ) x O y f (x) A B a b x y x M x x M y lim 1 0 M M M M x

s'(x)=V1+(y)月 ds=+()2dx ds=v(dx)2+(dy)2 若曲线由参数方程表示: x=x(t) y=0 永表示对参 数t的导数 则弧长微分公式为 ds=V2+少2d1 几何意义:ds=MT dx cosa sin a ds ds xx+dx x BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束
目录 上页 下页 返回 结束 则弧长微分公式为 ds x y d t 2 2 s (x) 2 1 ( y ) ds 1 ( y ) dx 2 或 2 2 ds (dx) (dy) O x dx dx x y x M dy T 几何意义: ds MT cos ; d d s x sin d d s y 若曲线由参数方程表示: ( ) ( ) y y t x x t 数 的导数 表示对参 t x

二、曲率及其计算 在光滑弧上自点M开始取弧段,其长为△s,对应切线 转角为c,定义 弧段△s上的平均曲率 K M △S 点M处的曲率 △C K lim da △S→0 △S ds 注意:直线上任意点处的曲率为0! BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 录 上页 返回 结束
目录 上页 下页 返回 结束 二、曲率及其计算 在光滑弧上自点 M 开始取弧段, 其长为 s , 对应切线 , 定义 弧段s上的平均曲率 s K M M s 点 M 处的曲率 s K s 0 lim ds d 注意: 直线上任意点处的曲率为 0 ! 转角为

例3.6.2求半径为R的圆上任一点处的曲率 解:如图所示 △S=R△a △a K=lim △-→0 △S R 可见:R愈小,则K愈大,圆弧弯曲得愈厉害; R愈大,则K愈小,圆弧弯曲得愈小 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 、 返回 结束
目录 上页 下页 返回 结束 例3.6.2 求半径为R 的圆上任一点处的曲率 . 解: 如图所示 , s R s K s 0 lim R 1 可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ; R 愈大, 则K 愈小 , 圆弧弯曲得愈小 . s R M M

曲率K的计算公式 da 设曲线弧y=f(x)二阶可导,则由 K ds ame=y(设-子a孕 得 a arctan y da (arctan y)'dx x 1+y2 又ds=V1+y2dx 故曲率计算公式为K= (1+y23 当y'<1时,有曲率近似计算公式K≈y" BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 下页返回 结束
目录 上页 下页 返回 结束 当 y 1时, 有曲率近似计算公式 tan y ) 2 π 2 π (设 得 arctan y d (arctan y )dx x y y d 1 2 ds 1 y dx 2 故曲率计算公式为 s K d d 2 3 (1 ) 2 y y K K y 又 曲率K 的计算公式 设曲线弧 y f (x) 二阶可导, 则由

*说明: (1)若曲线由参数方程 [x=x(t) ly=x(t) 给出,则 护- K=- 2+2)为 (2)若曲线方程为x=(y),则 K=- x" (1+x2)为 K=- y" (1+y2)为 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 返回 结束
目录 上页 下页 返回 结束 *说明: (1) 若曲线由参数方程 ( ) ( ) y y t x x t 给出, 则 2 3 (1 ) 2 y y K (2) 若曲线方程为 x ( y),则 2 3 (1 ) 2 x x K 2 3 ( ) 2 2 x y xy xy K

三、曲率圆 A(a,B) 设M为曲线C上任一点,在点 M处作曲线的切线和法线,在曲线 的凹向一侧法线上取点A使 M(x,y) 把以A为中心,R为半径的圆叫做曲线在点M处的 曲率圆(密切圆),R叫做曲率半径,A叫做曲率中心 在点M处曲率圆与曲线有下列密切关系 (1)有公切线; (2)凹向一致; (3)曲率相同 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 三、曲率圆 T y O x A(, ) R M (x, y) C 设 M 为曲线 C 上任一点 , 在点 在曲线 K AM R 1 把以 A 为中心, R 为半径的圆叫做曲线在点 M 处的 曲率圆 ( 密切圆 ) , R 叫做曲率半径, A 叫做曲率中心. 在点M 处曲率圆与曲线有下列密切关系: (1) 有公切线; (2) 凹向一致; (3) 曲率相同 . M 处作曲线的切线和法线, 的凹向一侧法线上取点 A 使

设曲线方程为y=f(x),且y”≠0,求曲线上点M处的 曲率半径及曲率中心A(,B)的坐标公式 设点M处的曲率圆方程为 (5-α)2+(7-B)2=R2 A(a,B) 故曲率半径公式为 1 R= 0+2)为 K y M(x,y) C,B满足方程组 (x-a)2+(y-B)2=R2 (M(x,y)在曲率圆上) x-a (AM⊥MT) y-B BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 设曲线方程为 y f (x), 且 y 0, 求曲线上点M 处的 曲率半径及曲率中心 A( , ) 设点M 处的曲率圆方程为 2 2 2 ( ) ( ) R 故曲率半径公式为 K R 1 2 3 (1 ) 2 y y , 满足方程组 2 2 2 (x ) ( y ) R (M (x, y)在曲率圆上) y (AM MT) y x 的坐标公式 . T y O x R M (x, y) C A(, )

*由此可得曲率中心公式 A(a,B) a=x-X(l+y2) y M(x,y) B=y+1+ (注意y-阝与y”异号) 当点M(x,y)沿曲线y=f(x)移动时,相应的曲率中心 的轨迹G称为曲线C的渐屈线, 曲线C称为曲线G的渐伸线 曲率中心公式可看成渐 屈线的参数方程(参数为x) 点击图中任意点动画开始或暂停 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束
目录 上页 下页 返回 结束 , 满足方程组 2 2 2 (x ) ( y ) R (M (x, y)在曲率圆上) y (DM MT) y x 由此可得曲率中心公式 y y y x (1 ) 2 y y y 2 1 (注意 y 与 y 异号 ) 当点 M (x , y) 沿曲线 y f (x)移动时, 的轨迹 G 称为曲线 C 的渐屈线 , 相应的曲率中心 曲率中心公式可看成渐 曲线 C 称为曲线 G 的渐伸线 . 屈线的参数方程(参数为x). 点击图中任意点动画开始或暂停 T y O x R M (x, y) C A(, ) *