
第一章 第2节 赵列的教限 数列极限的例子 二、数列与整标函数 三、数列的极限 四、数列极限的性质 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 第一章 二 、数列与整标函数 三 、数列的极限 一、数列极限的例子 第2节 数列的极限 四 、数列极限的性质
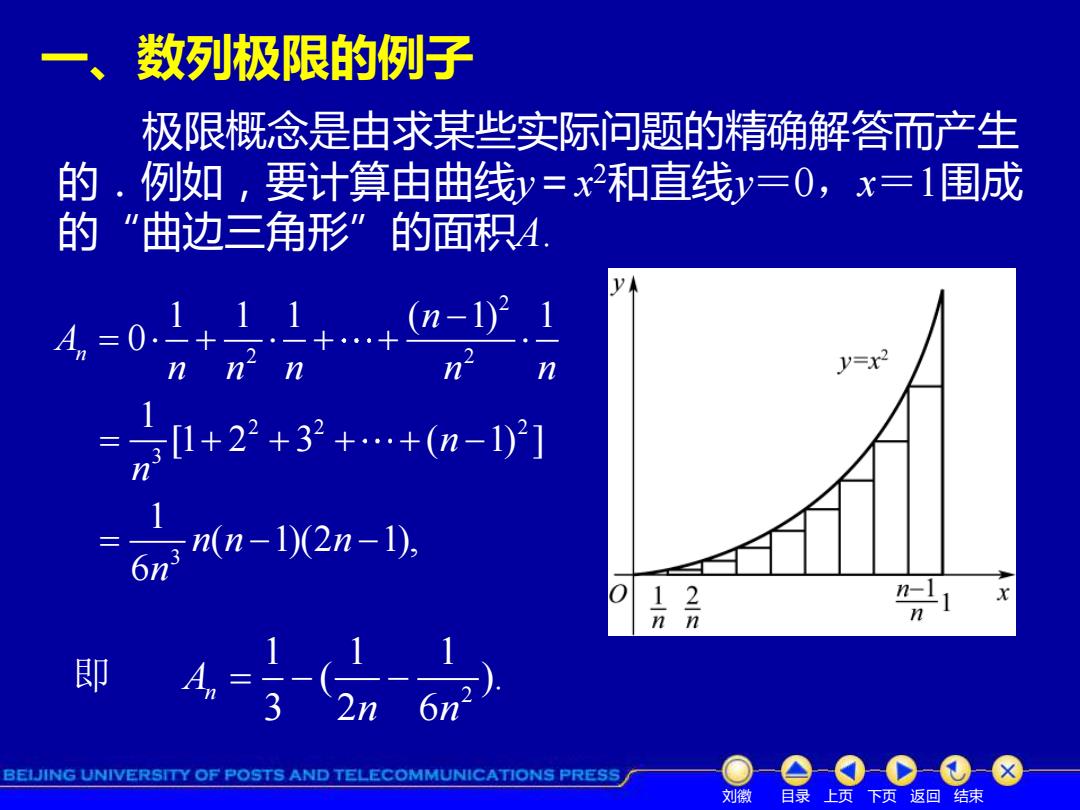
数列极限的例子 极限概念是由求某些实际问题的精确解答而产生 的.例如,要计算由曲线y=x2和直线y=0,x=1围成 的"曲边三角形”的面积4 4,=0.1+51+ (n-1)21 n' n V=x2 =31+22+32+…+(n-] 6mmn-12n-1), n n 27 n 即 4-3-no) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 刘徽 目录上页下页返回结束
目录 上页 下页 返回 结束 一、数列极限的例子 极限概念是由求某些实际问题的精确解答而产生 的.例如,要计算由曲线y=x 2和直线y=0,x=1围成 的“曲边三角形”的面积A. 刘徽 2 2 2 2 2 2 3 3 1 1 1 ( 1) 1 0 1 [1 2 3 ( 1) ] 1 ( 1)(2 1), 6 n n A n n n n n n n n n n n − = + + + = + + + + − = − − 2 1 1 1 ( ). 3 2 6 A n n n 即 = − −

台阶形面积是所分小段个数的函数.从图形上 看,台阶形面积随n的变化而变化,当n增大时,A,也 增大,但4,不会超过曲边三角形面积4,且随着的增 大,A越来越接近于A. 在这里,为了求不规则图形的面积,我们利用了 规则图形面积的极限.这就是用“极限方法”解决实 际问题的基本思想 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 台阶形面积是所分小段个数n的函数.从图形上 看,台阶形面积随n的变化而变化,当n增大时,An也 增大,但An不会超过曲边三角形面积A,且随着n的增 大,An越来越接近于A. 在这里,为了求不规则图形的面积,我们利用了 规则图形面积的极限.这就是用“极限方法”解决实 际问题的基本思想.

二、 数列与整标函数 般地,按照某种顺序排列起来的一串实数x1, X211Xn, 称为数列,简记为{x}或x(n= 1,2,3,…),其中每一个数叫做数列的项,第n项x叫 做数列的一般项或通项 11 (1)A2,A (4) (21, (5)1,-1,1,…,(-1)+1,… 14n+(-1)- (3)2,4,8,…,2 (62 23 n 以上都是数列的例子,其一般项分别为: BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 刘徽 目录上页下页返回结束
目录 上页 下页 返回 结束 二、数列与整标函数 刘徽 2 3 (1) , , , , 1 1 1 (2)1, , , , , 2 3 (3)2, 4,8, , 2 , n n A A A n 一般地,按照某种顺序排列起来的一串实数 x1, x2,…,xn,…,称为数列,简记为 或xn (n= 1,2,3,…),其中每一个数叫做数列的项,第n项xn叫 做数列的一般项或通项. xn 1 1 1 1 1 1 (4) , , , , , 2 4 8 2 (5)1, 1,1, ,( 1) , 1 4 ( 1) (6)2, , , , , 2 3 n n n n n + − − − + − 以上都是数列的例子,其一般项分别为: 1 1 1 ( 1) 1 , ,2 , ,( 1) , . 2 n n n n n n A n n − + + − −

在几何上,数列{x}表示数轴上的一列点x1,x2,… xn,…,如图所示 X, X 从函数的观点看,一个数列的通项x,可以看做某一 个函数当自变量取正整数时的函数值,即 xn=n)(n=1,2,…), 称为整标函数 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 在几何上,数列 表示数轴上的一列点x1,x2,…, xn,…,如图所示. xn 从函数的观点看,一个数列的通项xn可以看做某一 个函数当自变量取正整数n时的函数值,即 xn =f(n) (n=1,2,…), 称为整标函数.

三、数列的极限 定义设有数列{xn}, 如果对于任意给定的正数(无 论它多么小),总存在一个正整数N,使得当>N时 不等式 |xn-d恒成立,则称常数a为数列 的极 限,或称数列 收敛于a,记为 lim=a或xn→a(n>o) n->oo 如果数列{x}没有极限,就说数列{x}是发散的 为了表达方便,引入记号“”表示“对于任意 给定的”或者“对于每一个”,记号“3”表示“存 在 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 刘徽 目录上 下页返回结束
目录 上页 下页 返回 结束 三、数列的极限 刘徽 lim ( ). n n n x a x a n → = → → 或 定义 设有数列 ,如果对于任意给定的正数ε(无 论它多么小),总存在一个正整数N,使得当n>N时, 不等式 恒成立,则称常数a为数列 的极 限,或称数列 收敛 xn 于a,记为 xn | | n x a − xn 如果数列 没有极限,就说数列 是发散的. n x xn 为了表达方便,引入记号“∀”表示“对于任意 给定的”或者“对于每一个”,记号“∃”表示“存 在”.

例1.2.1用定义证明 y1 证lx,-a月 n+-1) 为了使1x,-a小于任意 n n 给定的正数,只要所以,>0,取 n v或v[卧当n时,就有 所以 lim n+1=1 n->o0 n BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例1.2.1 用定义证明 1 ( 1) lim 1 1. n x n − → − + = 证 为了使 小于任意 给定的正数ε,只要 所以,∀ε>0,取 当n>N时,就有 1 ( 1) 1 | | 1 , n n n x a n n − + − − = − = | | n x a − 1 1 n . n 或 1 1 N N( ), = 或 1 ( 1) 1 1 1 . n n n n N − + − − = 1 ( 1) lim 1. n n n n − → + − 所以 =

四、数列极限的性质 -C 1.唯一性 a+b 2 证:用反证法.假设1imx,n=a及lim=b,且aN,时, n->o∞ xn-a小kb2,从而xnN2时,有 n->oo xn-bkb2,从而xn>生 取N=max{N1,N2},则当n>N时,x,满足的不等式 矛盾,故假设不真!因此收敛数列的极限必唯一 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 − 2 3a b 2 2 b a n b a x a − − − − 四、数列极限的性质 证: 用反证法. 及 且 a b. 取 因 lim x a, n n = → 故存在 N1 , 从而 2 a b n x + 同理, 因 lim x b, n n = → 故存在 N2 , 使当 n > N2 时, 有 2 a b n x + 1. 唯一性 使当 n > N1 时, 假设 2 2 b a n b a x b − − − − n a b x + 2 2 3b−a 从而 2 a b n x + 矛盾, 因此收敛数列的极限必唯一. 取N = maxN1 , N2 , 则当 n > N 时, 故假设不真 ! n x 满足的不等式

例1.2.4 证明数列xn=(-1)+1(n=1,2,…)是发散的 证:用反证法 假设数列{xn}收敛,则有唯一极限a存在 取ε=2,则存在N,使当n>N时,有 a-3<xn<a+力 a a+ 但因xn交替取值1与-1,而此二数不可能同时落在 长度为1的开区间(a-3,a+2)内,因此该数列发散 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例1.2.4 证明数列 是发散的. 证: 用反证法. 假设数列 收敛 , 则有唯一极限 a 存在 . 取 , 2 1 = 则存在 N , 2 1 2 1 a − xn a + 但因 n x 交替取值 1 与-1 , ( , ) 2 1 2 1 a − a + 内, 而此二数不可能同时落在 长度为 1 的开区间 使当 n > N 时, 有 因此该数列发散

2.有界性 证:设1imxn=a,取e=1,则门N,当n>N时,有 n->00 xn-a<1,从而有 x (x,-a)+a<x-a+a<1+a 取 M=max,xx1+a 则有xn≤M(n=1,2,…). 由此证明收敛数列必有界 说明:此性质反过来不一定成立.例如 数列{(-1)y1}虽有界但不收敛 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 2. 有界性 证: 设 取 =1, 则 N , 当 n N 时, 从而有 xn − a + a 1+ a 取 M = max x1 , x2 , , xN ,1 + a 则有 x M ( n =1, 2 , ). n 由此证明收敛数列必有界. 说明: 此性质反过来不一定成立. 例如, 1 ( 1) + − n 虽有界但不收敛 . x − a 1, n 有 数列