
第入章 拉普拉斯变换

§8.1拉普拉斯变换定义 定义8.1设函数)当t≥0时有定义,而且积分 00 f(t)e-"dt 在复数s的某一个区域内收敛,则由此积分所确定的 函数记为 Fs-Lns∫f)e"dt 称为函数的t)的拉普拉斯变换式,F(s)称为t)的拉 普拉斯变换(或称为象函数) 若F(s)是)的拉普拉斯变换,则称)为F(s)的拉 普拉斯逆变换(或称为原象函数),记作 t)=L1[F可(t)
§8.1 拉普拉斯变换定义 定义8.1 设函数f(t)当 时有定义,而且积分 在复数s的某一个区域内收敛,则由此积分所确定的 函数记为 F(s)=L[f](s)= . 称为函数的f(t)的拉普拉斯变换式,F(s)称为f(t)的拉 普拉斯变换(或称为象函数). t 0 0 ( )e dst f t t − 0 ( )e dst f t t − 若F(s)是f(t)的拉普拉斯变换,则称f(t)为F(s)的拉 普拉斯逆变换(或称为原象函数),记作 f(t)= L-1 [F](t)

例8.1求阶跃函数u() 6?心6的拉苦拉斯空换 躲: e LLu(s)=fc "dr=- 三一 S 例8.2求函数t)=ea的拉普拉斯变换,其中a是复常数. 解:当Re(s>Re(a)时, )-Je"e 即】 e Re(s)>Re(a)
例8.1 求阶跃函数u(t)= 的拉普拉斯变换. 1, 0; 0, 0 t t 解: L[u](s)= 0 0 e 1 ( )e d st st f t t s s − − = − = 例8.2 求函数f(t)=eat的拉普拉斯变换,其中a是复常数. 解: 当Re(s)>Re(a)时, L[f](s)= ( ) 0 0 1 1 e e d e at st s a t s a s a − − − − = = − − 即 L[eatu(t)](s)= , Re(s)>Re(a) 1 s a −

例8.3求函数的拉普拉斯变换,其中n是正整数. 解:L[t四](s)=tedt 用分部积分法,得 n I"-1 S 0 所以有L[]=L["-], 当n=l时L[t(s)= 2 当n=2时,有L[t](s)= n! L[t](s)=
例8.3 求函数t n的拉普拉斯变换,其中n是正整数. 解:L[t n ](s)= 0 e d n st t t − 用分部积分法,得 1 1 0 0 0 e d e e d e d n n st st n st n st t n n t t t t t t s s s − − − − − − = − + = 所以有 L[t n ]= L[t n-1 ]. 当n=1时 L[t](s)= 2 1 s 当n=2时,有 L[t 2 ](s)= 3 2 s L[t n ](s)= 1 ! n n s +

定理8.1若函数t)满足下列条件: (1)在仑0的任意有限区间上分段连续; (2)存在常数心0与o≥0,使得 f(t)≤Meo,t>0 即当t→∞时,函数t)的增长速度不超过某一个指数 函数,ō称为函数t)的增长指数.则函数t)的拉普拉 斯变换 F()=「ft)e"dr 在半平面Re(s)>oo上存在,右端的积分在闭区域Re(s) ≥o>oo上绝对收敛且一致收敛,并且在半平面Re(s) >oo内,F(s)为解析函数
定理8.1若函数f(t)满足下列条件: (1) 在t0的任意有限区间上分段连续; (2) 存在常数M>0与00,使得 即当t→时,函数f(t)的增长速度不超过某一个指数 函数, 0称为函数f(t)的增长指数.则函数f(t)的拉普拉 斯变换 在半平面Re(s)> 0上存在,右端的积分在闭区域Re (s) > 0 上绝对收敛且一致收敛,并且在半平面Re (s) > 0 内,F(s)为解析函数. 0 ( ) e , 0 t f t M t 0 ( ) ( )e dst F s f t t − =
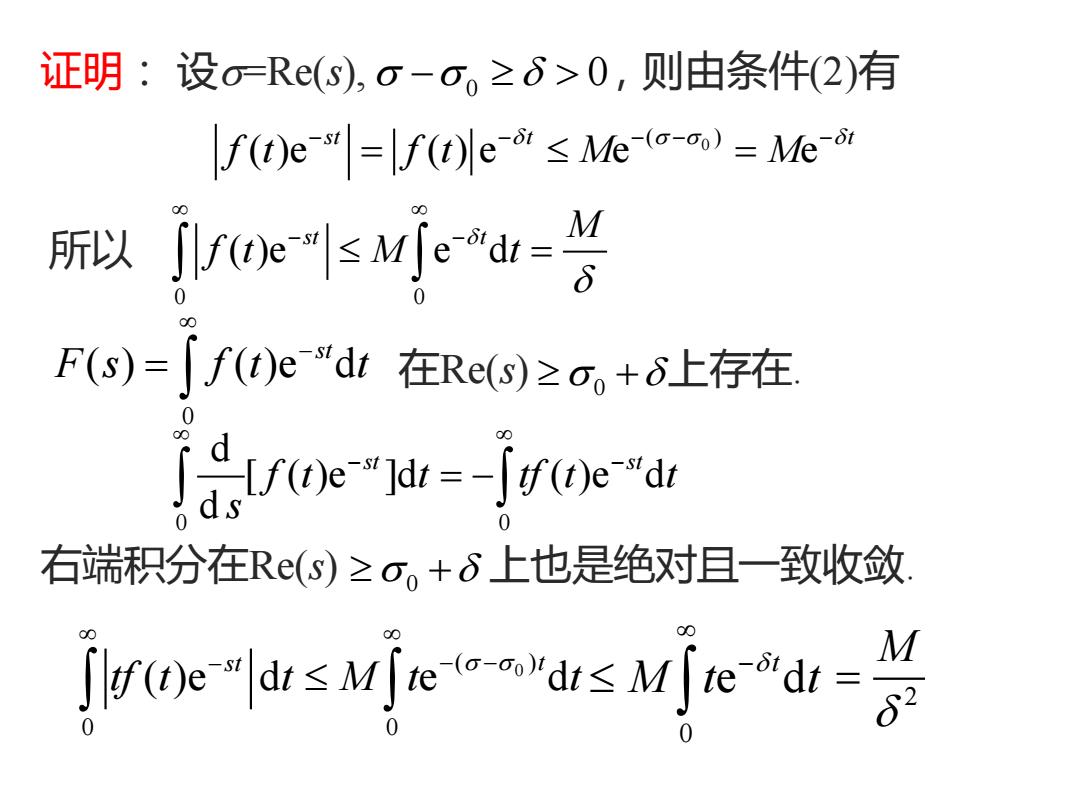
证明:设o-R(s),o-o。≥6>0,则由条件(2)有 f(u)e=f(le-m≤Meo-o)=Mea 所以- M F(s)=f(t)edt在Re(s)≥o。+6上存在 0 oe=-jgoeu 0 右端积分在R(s)≥o。+6上也是绝对且一致收敛 可= M
证明: 设=Re(s), − 0 0 ,则由条件(2)有 0 ( ) ( )e ( ) e e e st t t f t f t M M − − − − − = = 所以 0 0 ( )e e d st t M f t M t − − = + 0 0 ( ) ( )e dst F s f t t − = 在Re(s) 上存在. 0 0 d [ ( )e ]d ( )e d d st st f t t tf t t s − − = − 右端积分在Re(s) 上也是绝对且一致收敛. + 0 0 ( ) 0 0 ( )e d e d st t tf t t M t t − − − 0 e dt M t t − 2 M =

积分与微分的次序可以交换,于是有 品o=fwnean-jwe1u-joe*ar 由拉普拉斯变换的定义,得 F'(s)=L[(-t)f(t)](s) 所以F'(s)在R(s)≥o。+6上可导 由的任意性知,F(s在R(s)>o上存在,且为解析 函数.定理得证
积分与微分的次序可以交换,于是有 0 d d ( ) ( )e d d d st F s f t t s s − = 0 d [ ( )e ]d d st f t t s − = 0 ( ) ( )e d st t f t t − = − 由拉普拉斯变换的定义,得 F s t f t s ( ) L[( ) ( )]( ) = − 所以, F s ( ) 在 上可导. Re( ) 0 s + 由的任意性知, 在 上存在,且为解析 函数. 定理得证. F s( ) Re( ) 0 s

例8.4求正弦函数sin的拉普拉斯变换,其中为实数 解:当Re(s)>O时,有 ● [sin kt](s)=sin ktedt -st e Fg2+k(-y-sin-k-cosk) 0 k S2+k2 余弦函数cosk的拉普拉斯变换 c[cos() Re(s)>0
例8.4 求正弦函数sinkt的拉普拉斯变换,其中k为实数. 解:当 Re( ) 0 s 时,有 0 sin ( ) sin e d st kt s kt t − = L 2 2 0 e ( sin cos ) st s kt k kt s k − = − − + 2 2 k s k = + 余弦函数coskt的拉普拉斯变换 2 2 cos ( ) s kt s s k = + L Re( ) 0 s
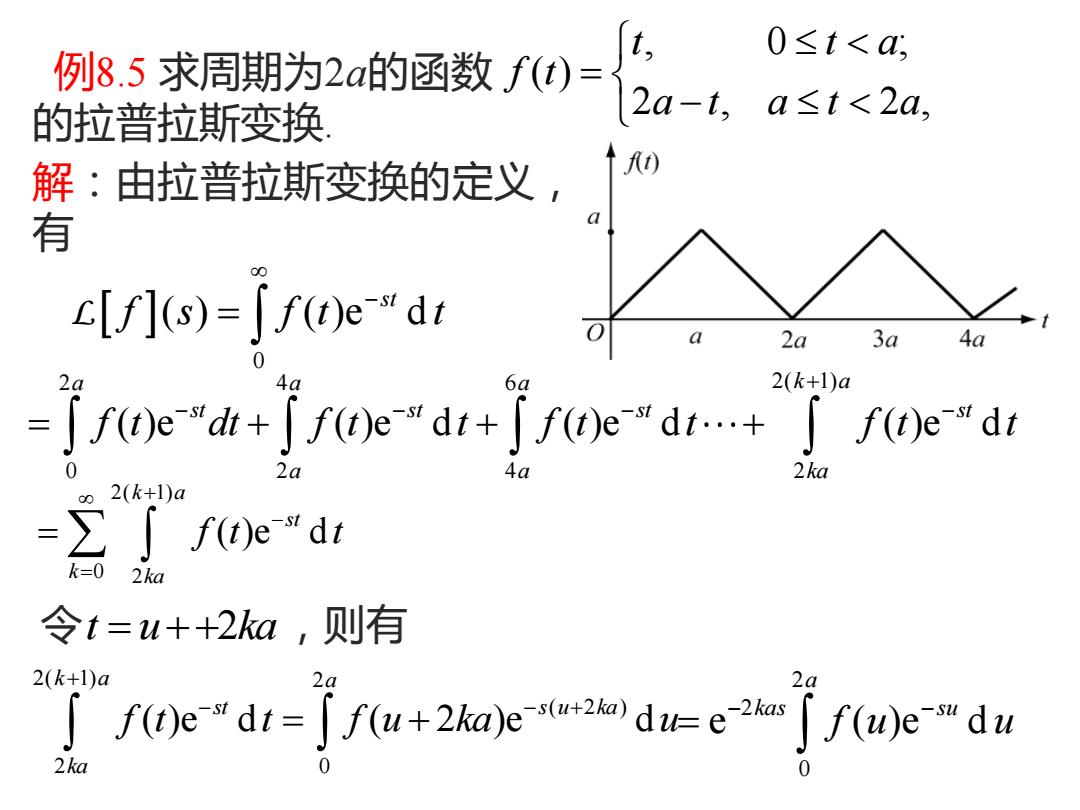
孙s5求周期为2的函数f0-2a-4,a51<2a, t, 0≤t<, 的拉普拉斯变换 解:由拉普拉斯变换的定义, 有 c[f]s)=∫f)e"dt 2a 3a 4a 2a 4a 6a 2(k+1)a "+fe+fedt+f(e"di 2a 2 ka 00 2(k+1)a ∑」f(t)edt k=0 2ka 令t=u++2ka,则有 2(k+1)a 2a 2a ∫f)e"dt=jfu+2ka)eu*adee2ka∫fw)e"du 2ka
例8.5 求周期为2a的函数 的拉普拉斯变换. , 0 ; ( ) 2 , 2 , t t a f t a t a t a = − 解:由拉普拉斯变换的定义, 有 0 ( ) ( )e d st f s f t t − = L 2 4 6 2( 1) 0 2 4 2 ( )e ( )e d ( )e d ( )e d a a a k a st st st st a a ka f t dt f t t f t t f t t + − − − − = + + + 2( 1) 0 2 ( )e d k a st k ka f t t + − = = 令 t u ka = + +2 ,则有 2( 1) 2 ( 2 ) 2 0 ( )e d ( 2 )e d k a a st s u ka ka f t t f u ka u + − − + = + 2 2 0 e ( )e d a kas su f u u − − =

根据函数的定义,有 2a udu=jedu+了rea-wed}a-e 0 2a 所以,c[f]s)=∑e2jfe"du k=0 2a -fuedu 记B=Re(s)当B>0时,有e2a=e2aB<1 因此有 1 = k=0 1-e-2as
根据函数的定义,有 2 2 0 0 0 ( )e d e d (2 )e d a a a su su su f u u u u f a u u − − − = + − 2 2 1 (1 e ) as s − = − 所以, 2 2 0 0 ( ) ( )e d a kas su k f s e f u u − − = = L 2 2 0 0 ( )e d e a su kas k f u u − − = = 记 = Re( )s . 当 0 时,有 2 2 e e 1 − − as a = 因此有 2 2 0 1 e 1 e kas as k − − = = −