
第九章 快速傅里叶变换

§9.1离散时间傅里叶变换 1.DTFT及DTFT的定义 离散时间傅里叶变换DTFT)及逆变换(DTFT) 的定义为 DTFT:X(e)=∑x(n)ema IT)-2元d 表示纯虚数单位,即是2=-1,X()是关于实数w的 一个复值函数,用直角坐标可以表示为: X(e)=Re(Y(e))+jIm(Y(e)): 用极坐标可以表示为: X(e)=Y(e)e)
§9.1 离散时间傅里叶变换 1. DTFT及IDTFT的定义 离散时间傅里叶变换(DTFT)及逆变换(IDTFT) 的定义为: DTFT: IDTFT: (e ) ( )e j jn X x n − − = π π 1 ( ) (e )e d 2π j jn x n X − = j表示纯虚数单位,即是j 2=-1, X(ejw)是关于实数w的 一个复值函数,用直角坐标可以表示为: 用极坐标可以表示为: (e ) Re( (e )) Im( (e )); j j j X X j X = + ( ) (e ) (e ) e j j j X X =

X(e)=X(e) 其中X(e°)称为幅度函数,0(o)称为相位函数,都是 关于o的实值函数.通常,也将傅里叶变换称为傅里叶 谱,相应地,将X(e)称为幅度谱,(o)称为相位谱 当相位函数相差2π时,它的傅里叶变换是保持 不变的即 X(e)=X(e)e)=Y(e)e2) 对任意一个傅里叶变换,相位函数是不能被唯 一确定的.一般地,假定相位函数(o)在区域[-π,) 内,该区域称为主值域
其中 称为幅度函数, 称为相位函数,都是 关于的实值函数.通常,也将傅里叶变换称为傅里叶 谱,相应地,将 称为幅度谱, 称为相位谱. (e ) j X ( ) (e ) j X ( ) ( ) (e ) (e ) e j j j X X = 当相位函数相差2k时,它的傅里叶变换是保持 不变的.即 ( ) ( ( ) 2 π (e ) (e ) e (e ) e ) j j j j j k X X X + = = 对任意一个傅里叶变换,相位函数是不能被唯 一确定的.一般地,假定相位函数 在区域 [-, ) 内,该区域称为主值域. ( )

2.DTFT的性质 设离散时间序列g(n),h(n),x(n)的离散时间傅里叶变换分 别为G(e/o)H(eo)和X(eo) (1)线性 设(n)=ag(n)+bh(n),则其离散时间傅里叶变换为 L(e)=aG(e)+bH(e) (2)平移性 a时移性 设l(n)=g(n-no),则其离散时间傅里叶变换为 L(e)=e jG(e). b.频移性 设(n)尸e,g(n),则其离散时间傅里叶变换为 L(e)=G(e)
2. DTFT的性质 设离散时间序列g(n),h(n),x(n)的离散时间傅里叶变换分 别为 G(e ) j , H(e ) j 和 (e ) j X (1)线性 设l(n)=ag(n)+bh(n),则其离散时间傅里叶变换为 (e ) (e ) (e ). j j j L aG bH = + (2)平移性 a.时移性 设l(n)=g(n-n0 ),则其离散时间傅里叶变换为 b.频移性 设l(n)= g(n),则其离散时间傅里叶变换为 0 (e ) e (e ). j j j n L G − = 0 e j n 0 ( ) (e ) (e ) j j L G − =

(3)频域微分性 设l(n)=ng(n),则其离散时间傅里叶变换为 L()= dG(e) (4)卷积性质 dw 设l(n)-g(n)h(n),则其离散时间傅里叶变换为 L(ejo)=G(e)H(e). (⑤)调制性质 设(n)-(n)h(n),则其离散时间傅里叶变换为 (e)=2元JGeH(eoaa (6)帕斯瓦尔关系 设h*(n)为h(n)的共轭,H*(eo为H(e的共轭,则 ∑gwh*w=2元J.Ge)H*(ea
(3)频域微分性 设l(n)=ng(n),则其离散时间傅里叶变换为 d (e ) (e ) d j j G L j = (4)卷积性质 设l(n)=g(n)h(n),则其离散时间傅里叶变换为 ( ) (e ) (e ). j j L ej G H = (5)调制性质 设l(n)=g(n)h(n),则其离散时间傅里叶变换为 π ( ) π 1 (e ) (e ) (e )d . 2π j j j L G H − − = (6)帕斯瓦尔关系 设h*(n)为h(n)的共轭, *(e ) 为 的共轭, 则 j H (e ) j H π π 1 ( ) *( ) (e ) *(e )d . 2π j j g n h n G H − − =

(7)对称性 a.复数序列的离散时间傅里叶变换的对称性 设xe(n)和xg(n)分别为x(n)的共轭对称和反共轭对称部分 和X(e分别为eo).的共轭对称和反共轭对称部分. 则有以下性质成立 )x(-n)的离散时间傅里叶变换为X(eo) i)x*(-n)的离散时间傅里叶变换为X*(eo) i)Re[x(n)的离散时间傅里叶变换为 Xe)=[X(c刃+X*(em)
(7)对称性 a.复数序列的离散时间傅里叶变换的对称性 设xcs(n)和xca(n)分别为x(n)的共轭对称和反共轭对称部分, 和 分别为 .的共轭对称和反共轭对称部分. 则有以下性质成立: i) x(-n)的离散时间傅里叶变换为 ; ii) x* (-n)的离散时间傅里叶变换为 ; iii) Re [x(n)]的离散时间傅里叶变换为 (e ) j X cs (e ) j X ca (e ) j X (e ) j X − *(e ) j X 1 (e ) [ (e )] *(e ) 2 j j j X X X cs − = +

iv)m(x(n)的离散时间傅里叶变换为 X(e)=X(e】-X*(e) v)x(n)的离散时间傅里叶变换为Re[X(eo】; vi)xea(n)的离散时间傅里叶变换为jlm[X(eo)]; b.实数序列的离散时间傅里叶变换的对称性 设xev(n),xod(n)分别是x(n)偶部和奇部.则有以下性 质成立 i)xev(n)的离散时间傅里叶变换为Re[X(eo)】; i过xo(n)的离散时间傅里叶变换为jm[X(e/o)】;
iv) jIm(x(n))的离散时间傅里叶变换为 v) xcs(n)的离散时间傅里叶变换为 ; vi) xca(n)的离散时间傅里叶变换为 ; 1 (e ) [ (e )] *(e ) 2 j j j X X X ca − = − Re[ (e )] j X Im[ (e )] j j X b.实数序列的离散时间傅里叶变换的对称性 设xev(n), xod(n)分别是x(n)偶部和奇部. 则有以下性 质成立: i) xev (n)的离散时间傅里叶变换为 ; ii) xod(n)的离散时间傅里叶变换为 ; Re[ (e )] j X Im[ (e )] j j X
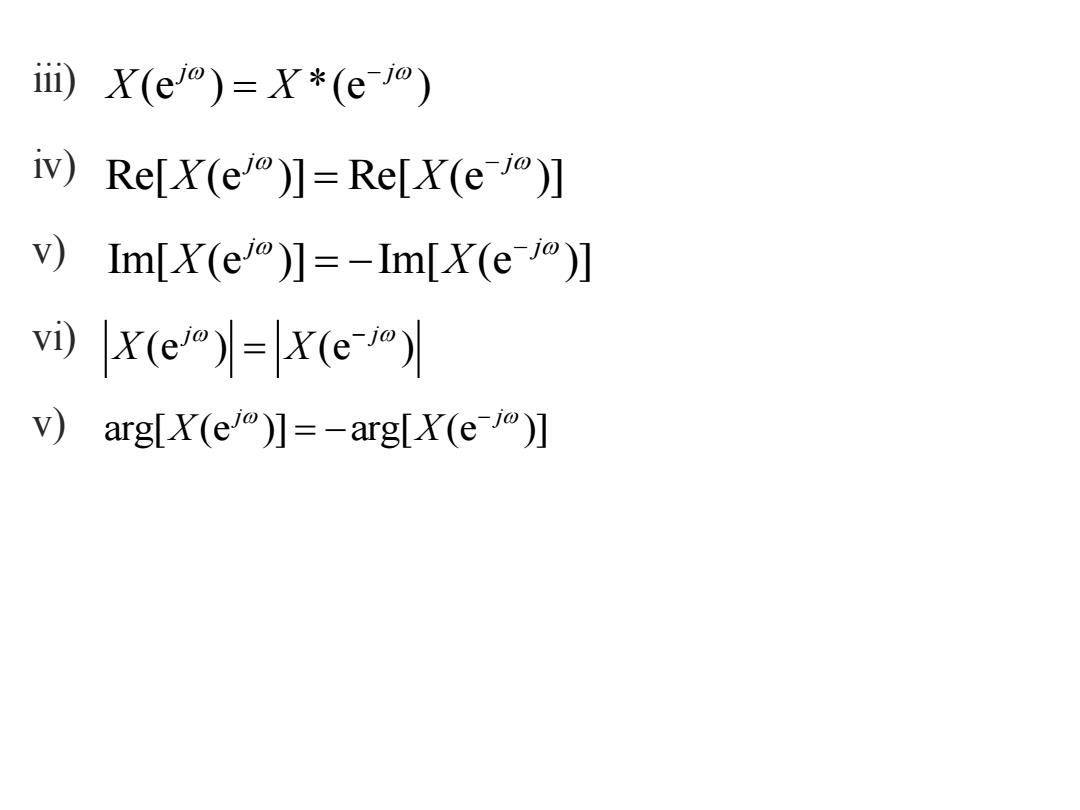
ii)X(ei)=*(e) iv)Re[X(e)]=Re[X(e)] v)Im[X(eo)】=-Im[X(eo)】 vi)X(e)=X(e-) V)arg[X(e)]=-arg[X(e)]
iii) iv) v) vi) v) (e ) *(e ) j j X X − = Re[ (e )] Re[ (e )] j j X X − = Im[ (e )] Im[ (e )] j j X X − = − (e ) (e ) j j X X − = arg[ (e )] arg[ (e )] j j X X − = −

3.Matlab的实现 在Matlab中可以使用内部函数freqz来进行离散时间 傅里叶变换 常用的格式主要有以下两种 H-freqz(num,den,w) 和 H=freqz(num,den,f,FT) 在H=freqz(num,den,w)中,w给出在0到之间的指定频 率集;在H=freqz(num,den,f,FT)中,向量指定了值必 须在0到FT/2之间的频率点,其中FT为采样频率
3. Matlab的实现 在Matlab中可以使用内部函数freqz来进行离散时间 傅里叶变换. 常用的格式主要有以下两种: H=freqz(num,den,w) 和 H=freqz(num,den,f,FT). 在H=freqz(num,den,w)中,w给出在0到之间的指定频 率集;在H=freqz(num,den,f,FT)中,向量f指定了值必 须在0到FT/2之间的频率点,其中FT为采样频率

§9.2变换简介 1.变换的定义 序列x(n)的Z变换X(z)的定义为 Xe=Z(x(n)=x(n)z” 其中实一个复变量, 设=reo,有 X(re)=∑x(n)r"eom, 2.逆变换的定义 定义逆变换为 x(n)=Z(()
§9.2 Z变换简介 1. Z变换的定义 序列x(n)的Z变换X(z)的定义为 X(z)=Z(x(n))= 其中z实一个复变量. ( ) n x n z − − 设z= re j ,有 ( e ) ( ) e . j n j n X r x n r − − − = 2. 逆Z变换的定义 定义逆Z变换为 x n Z X z ( ) ( ( )). − =