
第一章 复数和复平面

§1.1复数 1.复数的概念 形如z=a+ib或z=a+bi的数称为复数。 称为虚单位,即满足2=-1 α和b为实数,分别称为复数z的实部和虚部,记作 a=Rez,b=Imz. 当且仅当虚部b=0时,=a是实数; 当且仅当a=b=0时,z就是实数0; 当虚部b0时,叫做虚数; 当实部a=0且虚部b0时,=ib称为纯虚数 全体复数的集合称为复数集,用C表示 实数集R是复数集C的真子集
§1.1 复 数 1. 复数的概念 形如 z a b = +i 或 z a b = + i 的数称为复数。 a和b为实数,分别称为复数z的实部和虚部,记作 a z b z = = Re , Im . i称为虚单位,即满足 2 i = −1 •当且仅当虚部b=0时,z=a是实数; •当且仅当a=b=0时,z就是实数0; •当虚部b≠0时,z叫做虚数; •当实部a=0且虚部b≠0时,z=ib称为纯虚数. 全体复数的集合称为复数集,用C表示. 实数集R是复数集C的真子集
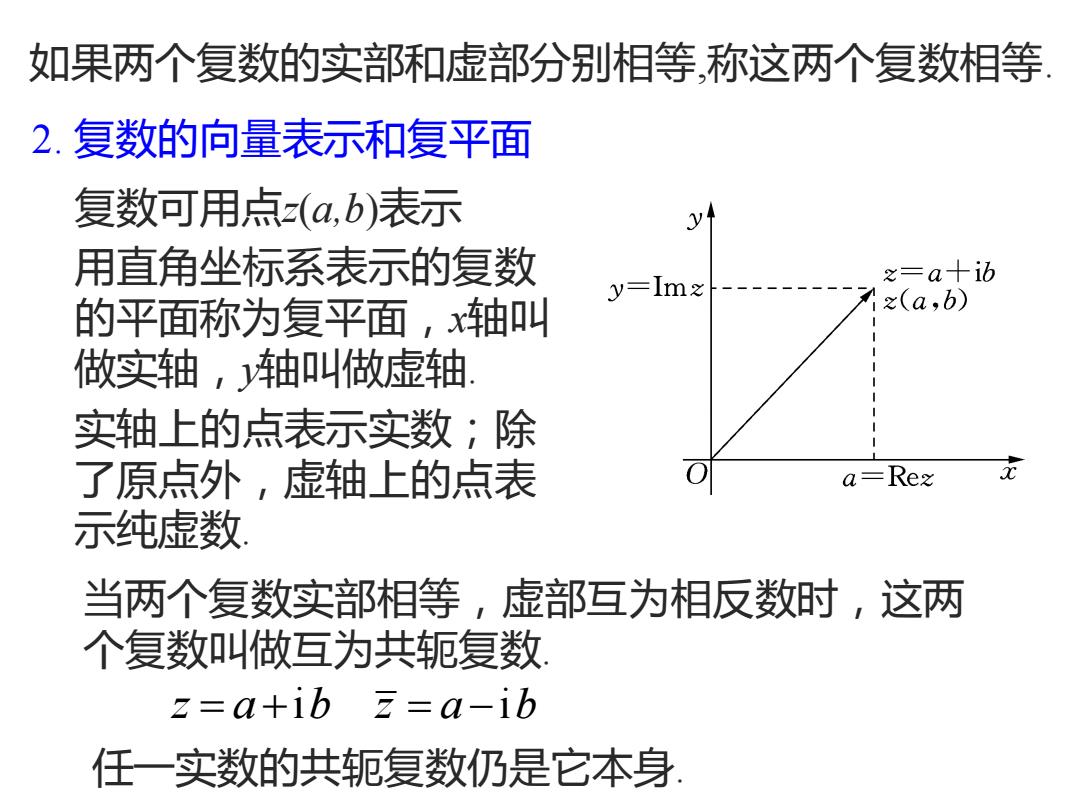
如果两个复数的实部和虚部分别相等,称这两个复数相等 2.复数的向量表示和复平面 复数可用点(a,b)表示 用直角坐标系表示的复数 y=Imz x=a十ib 的平面称为复平面,轴叫 升z(a,b) 做实轴,轴叫做虚轴 实轴上的点表示实数;除 了原点外,虚轴上的点表 a=Rex 示纯虚数 当两个复数实部相等,虚部互为相反数时,这两 个复数叫做互为共轭复数 z=a+ib z=a-ib 任一实数的共轭复数仍是它本身
如果两个复数的实部和虚部分别相等,称这两个复数相等. 2. 复数的向量表示和复平面 复数可用点z(a,b)表示 用直角坐标系表示的复数 的平面称为复平面,x轴叫 做实轴,y轴叫做虚轴. 实轴上的点表示实数;除 了原点外,虚轴上的点表 示纯虚数. 当两个复数实部相等,虚部互为相反数时,这两 个复数叫做互为共轭复数. z a b = +i z a b = −i 任一实数的共轭复数仍是它本身

在复平面上,复数z=a+ib还可以用由原点引向点z 的向量0z来表示,这种表示方式建立了复数集C与平面 向量Oz所成的集合的一一对应(实数0与零向量对 应).向量Oz的长度称为复数的模,记为或. lzl=r=Va2+b2≥0 Rez≤z≤Rez+lmzl,lImz≤lzl≤lRez+lImz. 3.复数的运算 复数的运算,有关复数的模和共轭 z,=c+id 复数的性质 z=a+ib,z,=c+id z =a+ib 加法 z1+22=(a+c)+(b+d) 减法 z1-22=(a-c)+i(b-d) 图1.2复数的加法
在复平面上,复数 还可以用由原点引向点z 的向量 来表示,这种表示方式建立了复数集C与平面 向量 所成的集合的一一对应(实数0与零向量对 应).向量 的长度称为复数z的模,记为 |z|或r . z a b = +i Oz Oz Oz 2 2 z = = + r a b 0 Re Re Re z z z + + z z z z z Im Im Im , . 3. 复数的运算 1 2 z a b z c d = + = + i , i 1 2 加法 z z a c i b d + = + + + ( ) ( ) 减法 1 2 z z a c i b d − = − + − ( ) ( ) 复数的运算,有关复数的模和共轭 复数的性质

乘法 zz2 ac+ibc+iad+ibd =(ac-bd)+i(bc+ad) lz2=z·2 除法 5atib (a+ib)(c-id) ac+bd bc-ad c+id 22 (c+id)(c-id) c2+d+ie2+d2,≠0 复数的模和共轭复数的性质 0Re:-e+m:-2点e- 21+网=E+,-写(得w*0叭 (3)w=zwl. (4) W bl (5)=z
乘法 2 1 2 z z ac bc ad bd ac bd bc ad = + + + = − + + i i i ( ) i( ) 2 z = z z 除法 1 2 2 2 2 2 2 i ( i )( i ) i , 0 i ( i )( i ) z a b a b c d ac bd bc ad z z c d c d c d c d c d + + − + − = = = + + + − + + 复数的模和共轭复数的性质 1 1 (1) Re ( ),Im ( ). 2 2i (2) ( ) , , ( 0). (3) . (4) . (5) . z z z z z z z z z w z w zw z w w w w zw w z z z w w z z = + = − + = + = = = = =
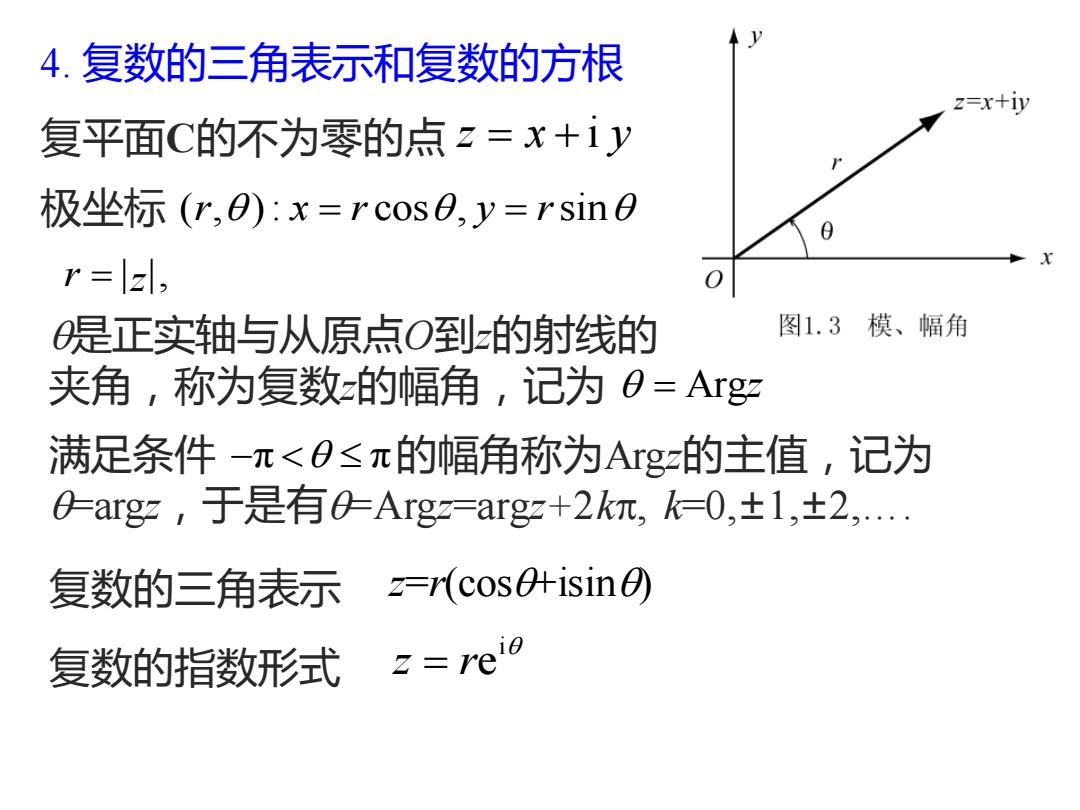
4.复数的三角表示和复数的方根 z=x+iy 复平面C的不为零的点z=x+1y 极坐标(r,O):x=rcos0,y=rsin8 r=el, 是正实轴与从原点O到z的射线的 图1.3模、幅角 夹角,称为复数z的幅角,记为0=Argz 满足条件-π<O≤π的幅角称为Agz的主值,记为 0arg,于是有0Arg=argz+2k饥,k-0,±1,±2,. 复数的三角表示=r(cos0升isin0 复数的指数形式 z=reio
4. 复数的三角表示和复数的方根 复平面C的不为零的点 z x y = + i 极坐标 ( , ) : cos , sin r x r y r = = r = z , 是正实轴与从原点O到z的射线的 夹角,称为复数z的幅角,记为 = Argz 满足条件 的幅角称为Argz的主值,记为 =argz,于是有=Argz=argz+2k, k=0,±1,±2,…. − π π 复数的三角表示 z=r(cos+isin) 复数的指数形式 i z re =

例1.1求Arg(-3-i4) 解:Arg(-3-i4)Farg(-3-i4)+2km,k=0,±1,±2,. 点-3-4位于第三象限 (-4) 4 arg(-3-i4)=arctan 元=arctan--π (-3) 3 4 Arg(-3-i4)=arctan。+(2k-l)π, =0,±1,±2,. 例1.2计算z=em 解:eπ=cosπ+isinπ=-l
例1.1 求Arg(-3-i4). 解: Arg(-3-i4)= arg(-3-i4)+2k, k=0,±1,±2,…. 点-3-i4位于第三象限 ( 4) 4 arg( 3 i 4) arctan π arctan π ( 3) 3 − − − = − = − − 4 Arg( 3 i 4) arctan (2 1)π, 3 − − = + −k k=0,±1,±2,…. 例1.2 计算 i π z = e i π 解: e cos = + = − π isin π 1

例1.3把复数V3+i表示成三角形式和指数形式 解:r=3+1-2,cos0= 2 √5+i对应的点在第一象限 ae5+)-8 5+1=2osg*1sn别 √5+i=2eim6
例1.3 把复数 3 i + 表示成三角形式和指数形式. 3 3 1 2,cos . 2 解: r = + = = 3 i + 对应的点在第一象限 π arg( 3 i) 6 + = π π 3 i 2 cos isin 6 6 + = + iπ/ 6 3 i 2e + =

复数乘法的几何意义 (cos +isin),2=(cose2 +isin). 2=r(cose +isin).(cose,+isine,) ((cos cose-sine sin)+i(sin cose+cose sin)) =(cos(,+02)+isin(02+02) z122=hei85e8=r3e(8+8), 322=3=322 Arg()=Arg=+Argz2. 两个复数相乘,积的模等于各复 数的模的积,积的幅角等于这两 个复数的幅角的和. 图1.4复数的乘法
复数乘法的几何意义 1 1 1 1 2 2 2 2 z r z r = + = + (cos isin ), (cos isin ). 1 2 1 1 1 2 2 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 2 2 (cos sin ) (cos isin ) ((cos cos sin sin ) i(sin cos cos sin )) (cos( ) isin( )) z z r i r r r r r = + + = − + + = + + + 1 2 1 2 i i i( ) 1 2 1 2 1 2 z z r r r r e e e . + = = 1 2 1 2 1 2 z z z z = = r r Arg( ) Arg Arg . 1 2 1 2 z z z z = + 两个复数相乘,积的模等于各复 数的模的积,积的幅角等于这两 个复数的幅角的和

322=53=l32 Arg(2)=Arg=1+Argz2. = 五5 ,Arg=Arg三+Arg2 2 21 Arg 22 5L=Args-Args2. 22 两个复数的商的模等于它们模的商,商的幅角 等于被除数的幅角与除数的幅角的差
1 1 1 2 1 2 2 2 ,Arg Arg Arg , z z z z z z z z = = + 1 1 1 1 2 2 2 2 ,Arg Arg Arg . z z z z z z z z = = − 两个复数的商的模等于它们模的商,商的幅角 等于被除数的幅角与除数的幅角的差. 1 2 1 2 1 2 z z z z = = r r Arg( ) Arg Arg . 1 2 1 2 z z z z = +