
概率论与数理统 第二章 随机变量 第一节 随机变量及其分布函数 第二节 离散型随机变量及其分布 第三节 连续型随机变量及其分布 第四节 随机变量函数的分布
第二章 随机变量 第一节 随机变量及其分布函数 第二节 离散型随机变量及其分布 第三节 连续型随机变量及其分布 第四节 随机变量函数的分布

概率论与数理统计 第一节【 随机变量及其分布函数 定义2.1设E是随机试验,它的样空间为2,如果对 2中每一个元素,有一个实数r()与之对应这样就 得到一个定义在2上的单值函数=X(),称之为 随机变量 定义2.2设X是一随机变量,x为任意实数,函数 F(x)=P{X≤x} 称为随机变量的分布函数。 上一页 下一页 返回
第一节 随机变量及其分布函数 定义2.1 称为随机变量X的分布函数。 定义2.2 设X是一随机变量,x为任意实数,函数 上一页 下一页 返回

概率论与数理统计 分布函数的基本性质: (1)F(x是一个单调不减函数; (2)0≤F(x)≤1,且IimF(x)=0,limF(x)=1; (3)F(x是右连续的。即对任意实数x,有 F(e+0)=F(x) 证明: (1)如x1<x2,则{X≤x}c{X≤x2,得: P{X≤x}≤P{X≤x2} F(x)≤F(x2) 上一页 下一页 返回
证明: 上一页 下一页 返回

概率论与数理统计 (2)由F(x)的定义易得0≤F(x)≤1。利用F(x)的单调性 为证,limF(x)=0,只要证1imF(-n)=0。考虑事件 An={X≤-n,n=1,2…,则An一A∩An=, 由概率的连续性得 lim F(x)=lim F(-n)=lim P(A) 11→十c0 00 =P(∩An)=0 n=1 极限imF(x)=1的类似证明 X)+00 上一页 下一页 返回
上一页 下一页 返回

概率论与数理统计 (3)由F(x的单调性,为证此性质只须证明: lim F(x+-)=F() 1→+o0 令An={X≤x+1,n=1,2,…, 则An一An∩An={X≤x}, n1 由概率的 连续性得: F(x+0)=imF(+)=lim) n n=1 =PX≤x}=F(e) 上一页 下一页 返回
由概率的 连续性得: 上一页 下一页 返回

概率论与数理统计 第二节 离散型随机变量及其分布 如果随机变量所有的可能取值为有限个或可数无 穷多个,则称这种随机变量为离散型随机变量。 设离散型随机变量X的可能取值为xk(k=1,2,…),事 件{X=X}发生的概率为pk,即 P(X=xg)=pr k=1,2,... 称为随机变量X的概率或分布律。 分布律常用表格 X x1 X2 .Xk… 形式表示如下: Pk 卫2 卫k… 上一页 下一页 返回
第二节 离散型随机变量及其分布 分布律常用表格 形式表示如下: X x1 x2 … xk… pk p1 p2 … pk… 如果随机变量所有的可能取值为有限个或可数无 穷多个,则称这种随机变量为离散型随机变量。 设离散型随机变量X的可能取值为xk (k=1,2,…),事 件 发生的概率为pk ,即 称为随机变量X的概率或分布律。 上一页 下一页 返回
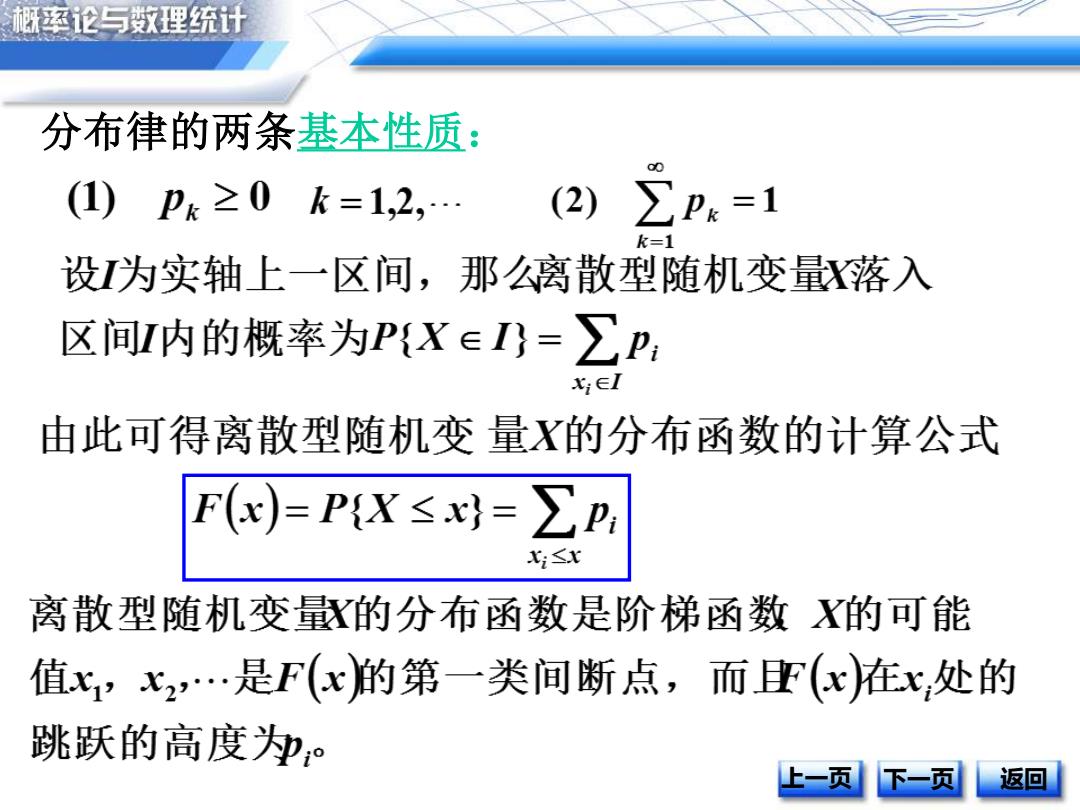
概率论与数理统计 分布律的两条基本性质: (1)pk≥0k=1,2,. (2) ∑Pk=1 K=1 设为实轴上一区间,那离散型随机变量落入 区间I内的概率为PX∈I)=∑p: x;∈I 由此可得离散型随机变量X的分布函数的计算公式 F(x)=PX≤x=p, X:≤x 离散型随机变量的分布函数是阶梯函数X的可能 值x,x2…是F(x的第一类间断点,而F(x在x,处的 跳跃的高度。 上一页 下一页 返回
分布律的两条基本性质: 上一页 下一页 返回
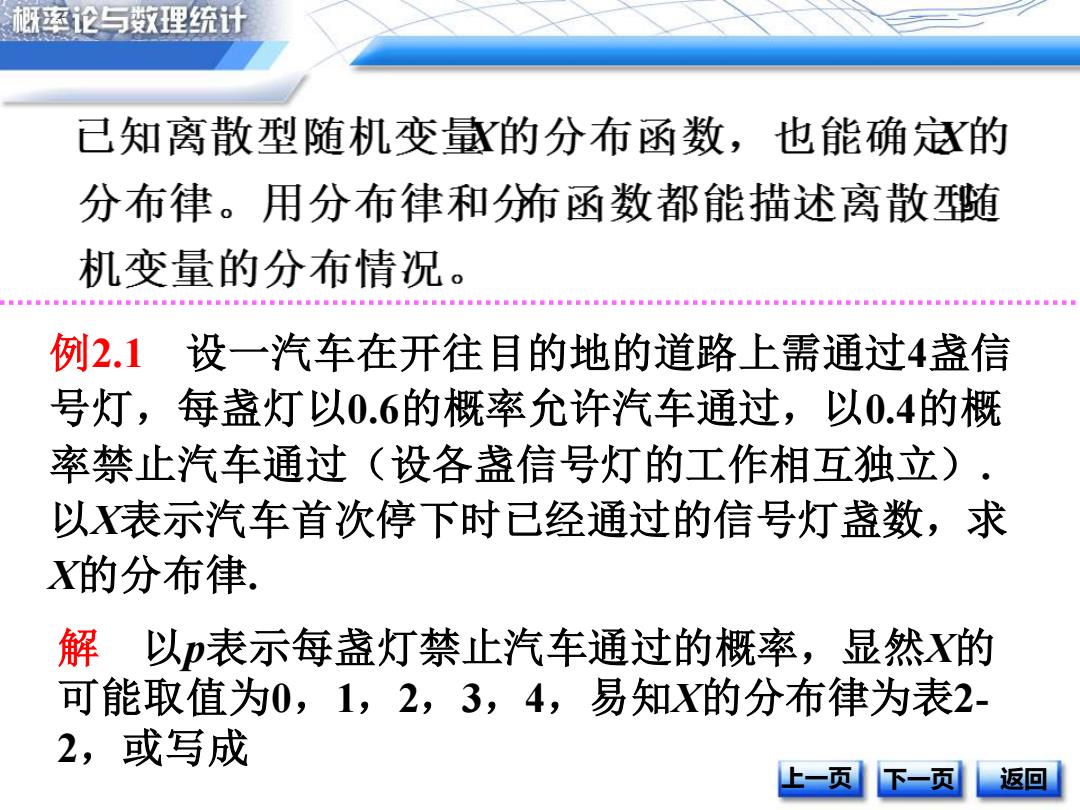
概率论与数理统计 己知离散型随机变量的分布函数,也能确的 分布律。用分布律和布函数都能描述离散随 机变量的分布情况 例2.1 设一汽车在开往目的地的道路上需通过4盏信 号灯,每盏灯以0.6的概率允许汽车通过,以0.4的概 率禁止汽车通过(设各盏信号灯的工作相互独立) 以表示汽车首次停下时已经通过的信号灯盏数,求 X的分布律 解以表示每盏灯禁止汽车通过的概率,显然X的 可能取值为0,1,2,3,4,易知X的分布律为表2- 2,或写成 上一页 下一页 返回
例2.1 设一汽车在开往目的地的道路上需通过4盏信 号灯,每盏灯以0.6的概率允许汽车通过,以0.4的概 率禁止汽车通过(设各盏信号灯的工作相互独立). 以X表示汽车首次停下时已经通过的信号灯盏数,求 X的分布律. 解 以p表示每盏灯禁止汽车通过的概率,显然X的 可能取值为0,1,2,3,4,易知X的分布律为表2- 2,或写成 上一页 下一页 返回
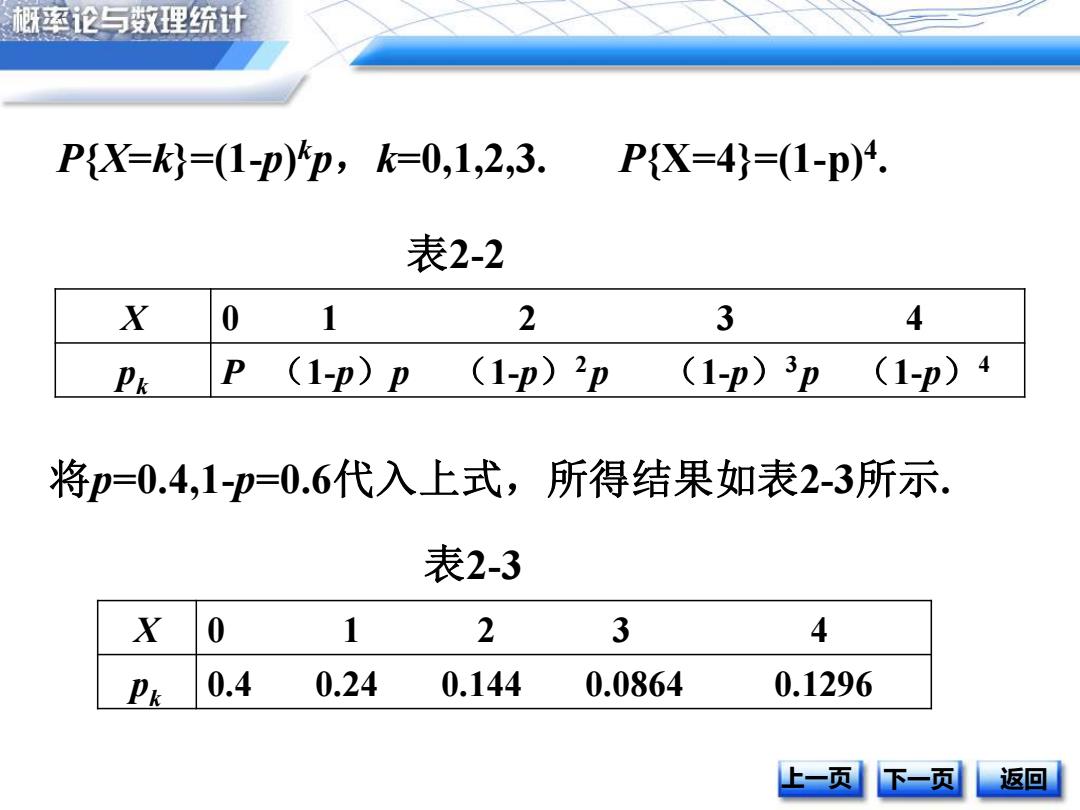
概率论与数理统计 P{X=k=(1-p)p,k=0,1,2,3. P{X=4}=(1-p)4. 表2-2 X 0 1 2 3 4 Pk P (1-p)p (1-p)2p (1-p)3p(1-p)4 将p=0.4,1-p=0.6代入上式,所得结果如表2-3所示. 表2-3 X 0 1 2 3 4 Pk 0.4 0.24 0.144 0.0864 0.1296 上一页 下一页 返回
P{X=k}=(1-p) kp,k=0,1,2,3. P{X=4}=(1-p)4 . 上一页 下一页 返回 表2-2 X 0 1 2 3 4 pk P (1-p)p (1-p)2 p (1-p)3 p (1-p)4 将p=0.4,1-p=0.6代入上式,所得结果如表2-3所示. 表2-3 X 0 1 2 3 4 pk 0.4 0.24 0.144 0.0864 0.1296

概率论与数理统计 1.两点分布 若在一次试验中X只可能取x1或x2两值(化1<x2), 它的概率分布是 P{X=x}=1-p(0<p<1), P{X=x2}=p, 则称X服从两点分布。 当规定x1=0,x2=1时两点分布称为(0一1)分布。 简记为X(0-1)分布。 X 0 1 Pk 1-p p 三下一页 返回
1.两点分布 若在一次试验中X只可能取x1 或x2 两值(x1<x2 ), 它的概率分布是 则称X服从两点分布。 当规定x1=0,x2=1时两点分布称为(0-1)分布。 简记为X~(0-1)分布。 X 0 1 pk 1-p p 上一页 下一页 返回