
第2为 第三章 洛必达法则 型和”型未定式 00 二、其他类型的未定式 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 二、其他类型的未定式 一、 型和 型未定式 0 0 第2节 洛必达法则 第三章

函数的性态 微分中值定理 导数的性态 本节研究: 函数之商的极限im 得型 00 转化 洛必达法则 导数之商的极限1im ∫'(x) g'(x) 将色达.6,手,4de BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 洛必达目录上页下页返回结束
目录 上页 下页 返回 结束 微分中值定理 函数的性态 导数的性态 函数之商的极限 导数之商的极限 转化 ( 或 型) 本节研究: 洛必达法则 洛必达

一、 0-0 型和 型未定式 定理1. 1)lim f(x)=lim g(x)=0 x→a x→a 2)f(x)与g(x)在U(a)内可导,且g(x)≠0 3) lim '(x) 存在(或为0) x->a g'(x) lim /(x) /(x) (或为无穷大) →a 8(x) xa g'(x) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 一、 '( ) ( ) 3) lim g x f x x a → 存在 (或为 ) '( ) ( ) lim ( ) ( ) lim g x f x g x f x x a x a = → → 2) f (x)与g(x) 在U(a)内可导, 定理 1. 型和 0 0 (或为无穷大) . 型未定式

定理条件:1)1imf(x)=limg(x)=0 X→a X→a 2)f(x)与g(x)在U(a内可导,且g'(x)≠0 3)lim f'(x) 存在(或为0) x→d 8(x) 证:无妨假设f(a)=g(a=0, 在指出的邻域内任取 x≠a,则f(x),g(x)在以a,x为端点的区间上满足柯 西中值定理条件,故 f(x)_f(x)-f(af'(5) (5在a,x之间) 8(x) g(x)-g(a) g(5) lim (x) lim f'(5)3) f'(x) x→d 8(x) x->a 8'(5) 8'(x) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 ( 在 a, x 之间) 证: 无妨假设 f (a) = g(a) = 0, 在指出的邻域内任取 则 在以a, x 为端点的区间上满足柯 故 ( ) ( ) ( ) ( ) ( ) ( ) g x g a f x f a g x f x − − = '( ) ( ) g f = '( ) ( ) lim g f x a = → 3) 定理条件: 西中值定理条件, '( ) ( ) 3) lim g x f x x a → 存在 (或为 ) 2) f (x)与g(x) 在U(a)内可导,

f'(x) 洛必达法则 lim f(x) x→ 8(x) x→a g'(x 推论1.定理1中x>a换为下列过程之一 x→a,X>a,x>0,x>+0,x→-0 条件2)作相应的修改,定理1仍然成立 推论2.若lim f'(x) 仍属9 x→ag(x) 型,且f"(x),g(x)满足定 理1条件,则 lim =m-=m ∫"(x) x→a 8(x) xa g'(x) x→a g"(x) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 定理1目录上页下页返回结束
目录 上页 下页 返回 结束 推论1. 定理 1 中 x →a 换为下列过程之一: , → − x a 推论2. 若 '( ) ( ) lim g x f x x a → 理1条件, 则 条件 2) 作相应的修改 , 定理 1 仍然成立. x → +, 洛必达法则 定理1
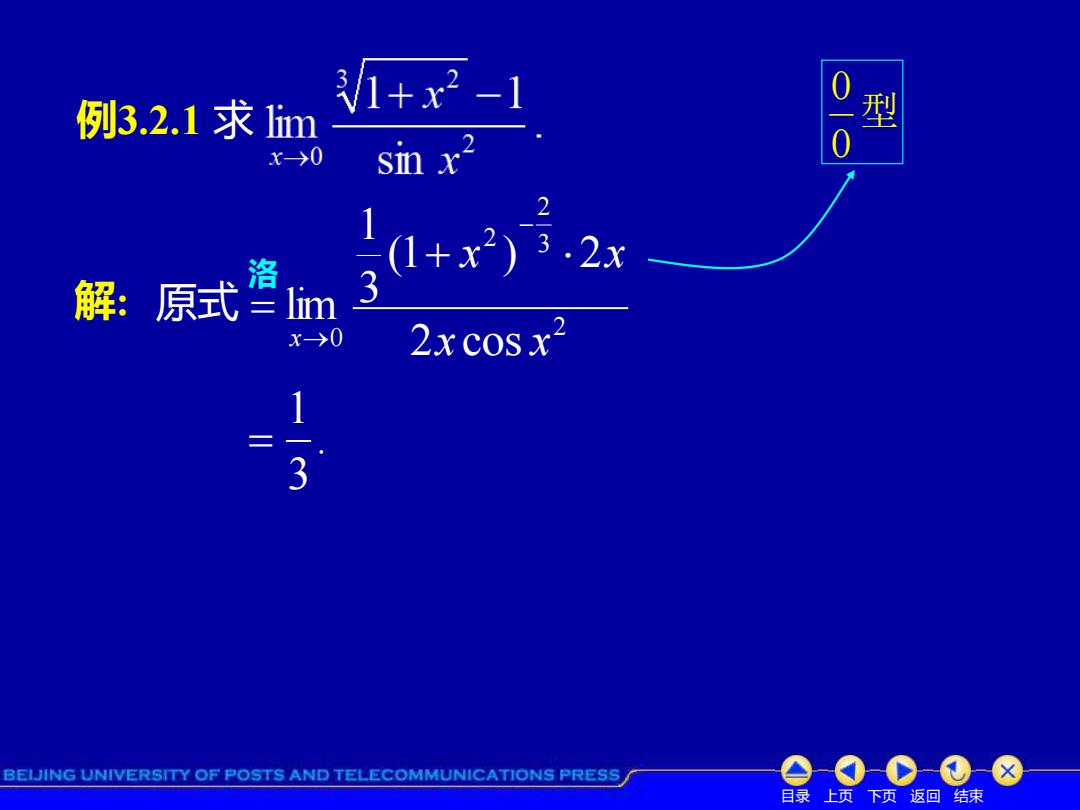
例3.2.1求1im 1+x2-1 型 x->0 sin x2 2 洛 解:原式lm x→0 2x cos x2 3 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS e-0-C-①8 目录上页下页返回结束
目录 上页 下页 返回 结束 例3.2.1 求 型 0 0 . 3 1 = 解: 原式 2 3 2 2 0 2 cos (1 ) 2 3 1 lim x x x x x + = − → 洛

ex-e *-2x 例3.2.2求1im x-→0 x-si x 解:im et-ex-2x e*+ex-2 ex-e-x lim lim x-→0 x-sin x x-→0 1-cosx x-→0 sin x lim e+e=2. x→0 cos x BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS e-0C⑨8 目录上页下页返回结束
目录 上页 下页 返回 结束 例3.2.2 求 解:

定理2. 1)lim f(x)=lim g(x)=0: x→00 2)f(x)与g(x)在x>N可导,且g(x)≠0 3)lim /"(x) 存在(或为o) x-→0g'(x) lim f(x) f'(x) (洛必达法则) g(x) g"(x) 证明与定理1相类似 注:对于x→a或x→o时 f(0为 型未定式 8(x) 00 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 '( ) ( ) 3) lim g x f x x → 存在 (或为∞) . '( ) ( ) lim ( ) ( ) lim g x f x g x f x x x a = → → 定理 2. 证明与定理1相类似. (洛必达法则) 2) f (x)与g(x) 在x N可导, 注:对于x→a或x→∞时 型未定式. 为 ( ) ( ) g x f x

例3.2.6求1im x (n>0,2>0) 型 解:(1)n为正整数的情形 原式=lim nxh-l 渣 Aeix lim n(n-l)xn-2 x>十+00 X→十00 22e2 谄. lim nl =0 x->+00 A"eix BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS ◆0-C-①8 目录上页下页返回结束
目录 上页 下页 返回 结束 例3.2.6 求 解: (1) n 为正整数的情形. 原式 = 0 x n x nx e lim −1 →+ = x n x n n x e ( 1) lim 2 −2 →+ − = ( 0). e lim →+ n 0 , x x n x 型 洛 n x x n e ! lim →+ == 洛 洛

例3.2.6求1im x” (n>0,元>0) X→十00 e (2)n不为正整数的情形 存在正整数k,使当x>1时 xk x"<xhtl 从而 用夹逼准则 。2x 由(1) lim lim X→+00 lim 。x BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例3.2.6 求 ( 0). e lim →+ n 0 , x x n x (2) n 不为正整数的情形. n x 从而 x n x e x k x e x k x e +1 由(1) 0 e lim e lim 1 = = + →+ →+ x k x x k x x x 0 e lim = →+ x n x x 用夹逼准则 k x +1 k x 存在正整数 k , 使当 x > 1 时