
第4章 不定积分 微分法:F'(x)=(?) 互逆运算 积分法:(?)Y=f(x))
第4章 微分法: F(x) = ( ? ) 积分法: ( ? ) = f (x) 互逆运算 不定积分

第1节 第四章 不定积分的桡念与性质 原函数与不定积分的概念 二、基本积分表 三、不定积分的性质 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 二、 基本积分表 三、不定积分的性质 一、 原函数与不定积分的概念 第1节 不定积分的概念与性质 第四章

原函数与不定积分的概念 实例:如果已知物体的直线运动方程为s=),则此 物体的运动速度是距离s对时间的导数.反过来 如果已知物体的运动速度是时间的函数y=v(),求 物体的运动方程s=),即求孔),使它的导数f()等 于已知函数() 定义1.若在区间I上定义的两个函数F(x)及f(x) 满足F'(x)=f(x)或dF(x)=f(x)dx,则称F(x)为f(x) 在区间I上的一个原函数 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 一、 原函数与不定积分的概念 实例: 如果已知物体的直线运动方程为s=f(t),则此 物体的运动速度v是距离s对时间t的导数.反过来, 如果已知物体的运动速度v是时间t的函数v=v(t),求 物体的运动方程s=f(t),即求f(t),使它的导数f′(t)等 于已知函数v(t). 定义 1 . 若在区间 I 上定义的两个函数 F (x) 及 f (x) 满足 在区间 I 上的一个原函数. 则称 F (x) 为f (x)

问题: 1.在什么条件下,一个函数的原函数存在? 2.若原函数存在,它如何表示? 原函数存在定理 若函数f(x)在区间I上连续, 则f(x)在I上存在原函数 (下章证明) 初等函数在定义区间上连续 初等函数在定义区间上有原函数 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 问题: 1. 在什么条件下, 一个函数的原函数存在 ? 2. 若原函数存在, 它如何表示 ? 原函数存在定理 存在原函数 . 初等函数在定义区间上连续 初等函数在定义区间上有原函数 (下章证明)

注.若F(x)是f(x)的一个原函数,则f(x)的所有 原函数都在函数族F(x)+C(C为任意常数)内 证:1)(F(x)+C)'=F'(x)=f(x) ∴.F(x)+C是f(x)的原函数 2)设Φ(x)是f(x)的任一原函数,即 Φ'(x)=f(x) 又知 F'(x)=f(x) ∴.[Φ(x)-F(x)]'=Φ'(x)-F'(x)=f(x)-f(x)=0 故 Φ(x)=F(x)+C(C0为某个常数) 它属于函数族F(x)+C BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 注. 原函数都在函数族 ( C 为任意常数 ) 内 . 证: 1) 又知 [(x) − F(x)] =(x) − F(x) = f (x) − f (x) = 0 故 0 (x) = F(x) +C ( ) C0为某个常数 它属于函数族 F(x) +C . 即

定义2.f(x)在区间I上的原函数全体称为f(x)在1 上的不定积分,记作f(x)dx,其中 「一积分号; f(x)一被积函数; (P120 x一积分变量;f(x)dk一被积表达式. 若F'(x)=f(x),则 「f(x)d=F(x)+C(C为任意常数) 例如, [e*dx=e*+C C称为积分常数, 「x2d=x3+C 不可丢! sin xdx cosx+C BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 定义 2. 在区间 I 上的原函数全体称为 上的不定积分, 其中 — 积分号; — 被积函数; — 积分变量; — 被积表达式. (P120) 若 则 ( C 为任意常数 ) C 称为积分常数, 不可丢 ! 例如, = x x e d C x e + = x dx 2 x +C 3 3 1 = sin xdx − cos x +C 记作

不定积分的几何意义: f(x)的原函数的图形称为f(x)的积分曲线 f(x)dx的图形 f(x)的所有积分曲线组成 的平行曲线族 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 不定积分的几何意义: 的原函数的图形称为 f (x)dx 的图形 的所有积分曲线组成 的平行曲线族. y O x0 x 的积分曲线
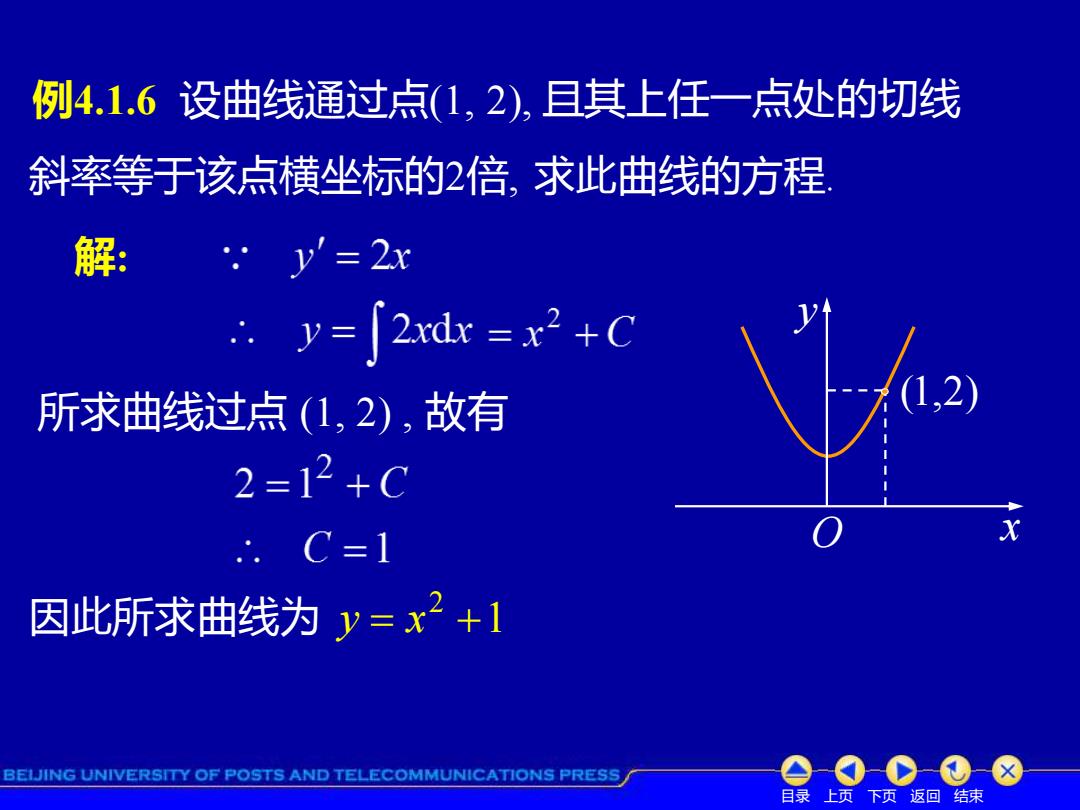
例4.1.6 设曲线通过点(1,2),且其上任一点处的切线 斜率等于该点横坐标的2倍,求此曲线的方程 解: .·y=2x .y=∫2dr=x2+C 所求曲线过点(1,2),故有 1,2 2=12+C C=1 因此所求曲线为y=x2+1 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例4.1.6 设曲线通过点(1, 2), 且其上任一点处的切线 斜率等于该点横坐标的2倍, 求此曲线的方程. 解: 所求曲线过点 (1, 2) , 故有 因此所求曲线为 1 2 y = x + y x (1,2) O

从不定积分定义可知 0) [J=-)或djra]Fa (2) ∫F'(x)dr=F(x)+C或∫dF(x)=F(x)+C 二、 基本积分表P122) 利用逆向思维 kdx kx+C (k是常数) (2) ∫rd=在x++C(k≠-) ()=1nx+C x<0时 (Inx)'=[In(-x)]'= X BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 d x d (1) f (x)d x = f (x) 二、 基本积分表 (P122) 从不定积分定义可知: d 或 f (x)dx = f (x)dx x = +C (2) F(x) d F(x) 或 = +C d F(x) F(x) 利用逆向思维 = (1) kdx kx +C ( k 是常数) = x x k (2) d x C k k + + + 1 1 1 = x d x (3) ln x +C x 0时 (k −1) (ln x ) = [ln(−x)] x 1 =

dx (4) arctanx+C-arccot x+C 1+X (5) dx arcsinx+C-arccosx+C (6) cos xdx sinx+C (7 sin xdx -cos x+C (8) j、-jca=nC (9) 「jox=-m+C BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 = + 2 1 d (4) x x arctan x +C = (6) cos xdx sin x +C = x x 2 cos d (8) = sec xdx 2 tan x +C 或 − arccot x +C = − 2 1 d (5) x x arcsin x +C 或 − arccos x +C = (7) sin xdx − cos x +C = x x 2 sin d (9) = csc xdx 2 − cot x +C