北京邮电大学出版社：21世纪高等学校规划教材《高等数学》课程教学资源（PPT课件讲稿）第4章 不定积分 2第一类换元积分法

第四章 第2为 第一类换元积分法 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束

目录 上页 下页 返回 结束 第2节 第一类换元积分法 第四章

基本思路 设F'(u)=f(W,u=2(x)可导，则有 dF[e(x)]=f[o(x)]o'(x)dx .∫fo(x】p'(x)dx=F[p(x]+C=F(u+Cu=ox =∫f(a)duue=ox) 第一类换元法 「flo(x)]p'(x)dx 第二类换元法 J∫fa)du BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 录 上负 返回 结束

目录 上页 下页 返回 结束 第二类换元法 第一类换元法 f [(x)](x)dx  f (u)du  基本思路 设 F(u)  f (u), u (x) 可导,     f [(x)] (x)dx F[(x)]C ( ) ( )d u x f u u    ( ) ( ) C u x F u    dF[(x)]  f [(x)](x)dx 则有

定理设F(u)是f()的一个原函数，且u=p(x)可导， 那么F[o(x]是f[p(x)]op(x)的原函数，即有换元公式 jIo(x】o'xdr=∫fuwu u=p(x) 即 ∫fp(xp'(x=∫f(o(x)ap(x) (也称配元法，凑微分法) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下 返回 结束

目录 上页 下页 返回 结束 定理 设F(u)是 f (u)的一个原函数,且u  (x)可导,    f [(x)] (x)dx  f (u)du u (x)  f ((x))d(x) (也称配元法 即    f [(x)] (x)dx , 凑微分法) 那么F[(x)]是 f [(x)] '(x)的原函数,即有换元公式

例42.7求∫tanxdx 解：∫anxd=∫dx=-j dcosx cos x cos x -In cosx C 同理 col sinx In sinx +C BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 自录上页 下负返回 结束

目录 上页 下页 返回 结束 例4.2.7 求 tan d .  x x 解:  x x xd cos sin    x x cos dcos  ln cos x C cot d  ?  x x  x x x sin cos d  ln sin x C   x x sin dsin   tan xdx 同理

例4.2.8求 dx 想到公式 du 条j dx arctan u C 令u=,则du=1dx a a arctan u C -aretan()+C BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 自录上页 下返回 结束

目录 上页 下页 返回 结束 2 2 1 d 1 ( ) x a x a    例4.2.8 求   . d 2 2 a x x 解:   2 2 d a x x , a x 令 u  则 x a u d 1 d    2 1 u du a 1 u C a  arctan  1 C a x a  arctan( )  1 想到公式   2 1 d u u  arctan u  C ( ) x a 

29求。o>0 dx 解： 1。 X arcsin n*+C a 想到 du arcsinu C [fo(x)]o'(x)dx=[f(p(x)dp(x) (直接配元 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 返回 结束

目录 上页 下页 返回 结束 例4.2.9 求    ( 0). d 2 2 a a x x    2 1 d u u 想到 arcsin u  C 解: 2 d 1 ( ) x a x a      f ((x))d(x) (直接配元)  f [(x)] (x)dx 2 d( ) 1 ( ) x a x a    C a x  arcsin     2 2 d a x x

例4.2.10求 ) dx 解： 1 x2-a2 +a--0=（1-1) 2a (x-a)(x+a) 2a'x-a x+a 原式= 。小] -] =2a[In x-al-Inxtall+C-2a x-a +C x+a BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束

目录 上页 下页 返回 结束 C x a x a a     ln 2 1 例4.2.10 求 ( 0). d 2 2    a x a x 解: 2 2 1 x  a  (x  a)(x  a) (x  a)  (x  a) 2a 1  ) 1 1 ( 2 1 a x a x  a    ∴ 原式 =    2a 1      x a x x a dx d        2a 1    x a d(x a)    2a 1  ln x  a  ln x  a C     x a d(x a)

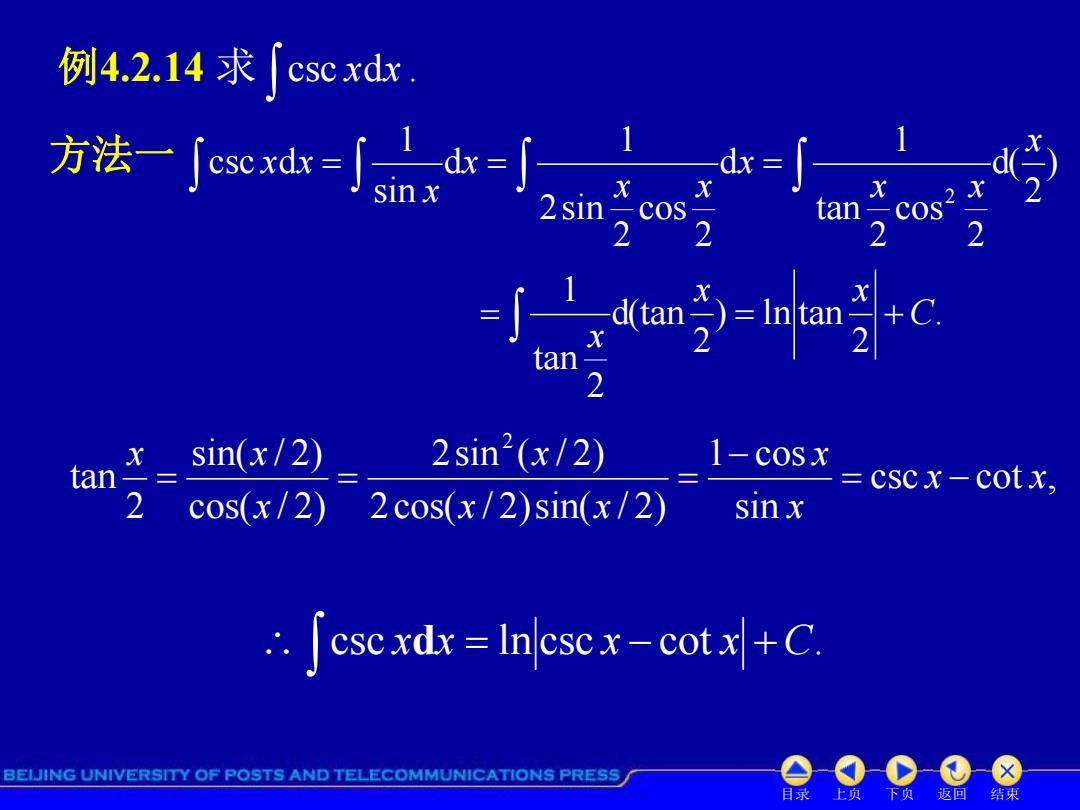
例4.2.14求csc xdx - 2 tan-cos 2 2 =j之dtem宁-n斗c tan sin(x/2) 2sin2(x/2) 1-cosx tan cscx-cotx, 2 cos(x/2) 2cos(x/2)sin(x/2) sinx cscxdx Incscx-cotx+C. BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 返回 结束

目录 上页 下页 返回 结束 例4.2.14 求 csc d .  x x 方法一        ) 2 d( 2 cos 2 tan 1 d 2 cos 2 2sin 1 d sin 1 csc d 2 x x x x x x x x x x . 2 ) ln tan 2 d(tan 2 tan 1 C x x x     csc cot , sin 1 cos 2cos( / 2)sin( / 2) 2sin ( / 2) cos( / 2) sin( / 2) 2 tan 2 x x x x x x x x x x        csc x x  ln csc x  cot x C.  d

解法二 2 sin +cos fo r=∫ 2 X 2sm2c02 2c02 sin-cos -jwr9-w如c enam月c--owtc BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 自录上负 下返回 结束

目录 上页 下页 返回 结束 解法 二 ) 2 d( 2 cos 2 sin 2 cos 2 sin d 2 cos 2 2sin 1 d sin 1 csc d 2 2 x x x x x x x x x x x x         C x x x x x        2 ln sin 2 ) ln cos 2 )d( 2 cot 2 (tan ln csc cot . 2 ln tan C x x C x     

解法三 xd-小==s 应用积分公式(18)得 d(cosx)incosx-1 cos'x-172cosx+1 +C Inescx-cotx+C. 同理可证 sec xdx =In secx+tanx+C. BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 、 返回 结束

目录 上页 下页 返回 结束 解法三 . cos 1 d(cos ) d sin sin d sin 1 csc d    2  2     x x x x x x x x x 同理可证  sec xdx  ln sec x  tan x C. 应用积分公式(18)得 ln csc cot . cos 1 cos 1 ln 2 1 cos 1 d(cos )  2         C x x C x x x x