北京邮电大学出版社：21世纪高等学校规划教材《高等数学》课程教学资源（PPT课件讲稿）第5章 定积分 1定积分的概念

第5章 定积分 不定积分 积分学 定积分

第5章 定积分 积分学 不定积分 定积分

第1为 第五章 定积分的桡念 一、引例 二、 定积分定义 三、定积分的几何意义 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页 返回 结束

目录 上页 下页 返回 结束 第1节 一、引例 二、 定积分定义 三、 定积分的几何意义 定积分的概念 第五章

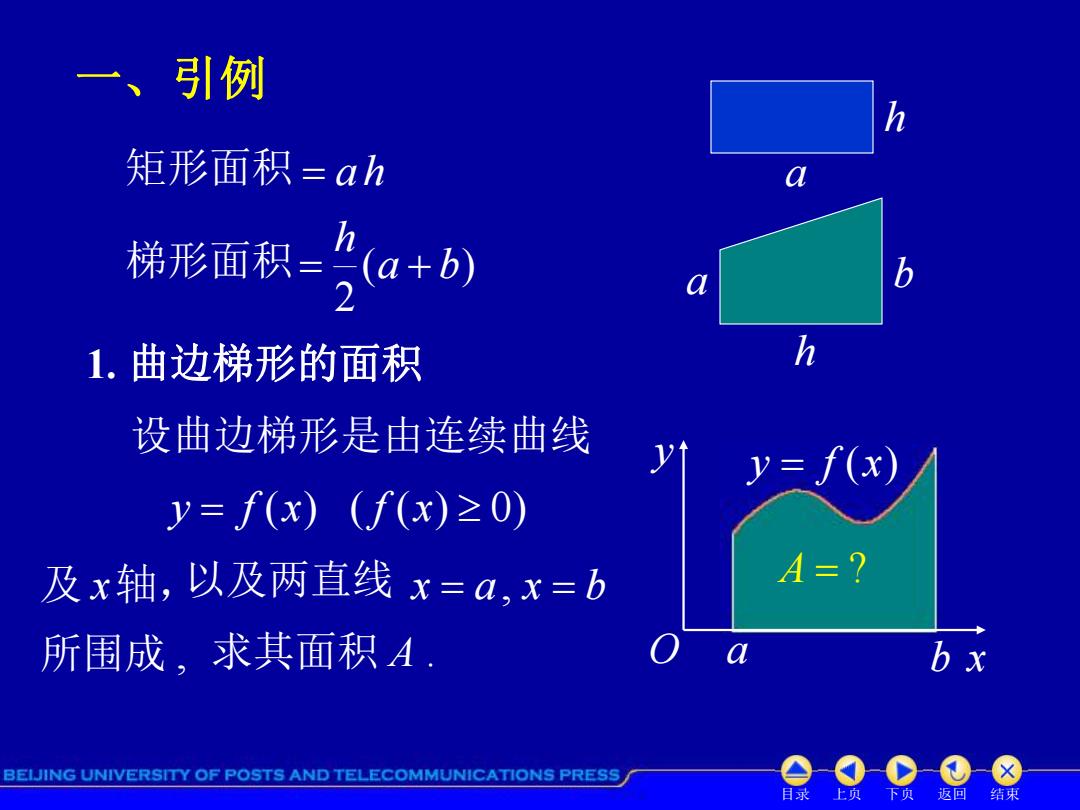
一、引例 矩形面积=ah 梯形面积-身a+) b 1.曲边梯形的面积 h 设曲边梯形是由连续曲线 y y=f(x) y=f(x)(f(x)≥0) 及x轴，以及两直线x=a,x=b A=? 所围成，求其面积A: a bx BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上负 下 返回 结束

目录 上页 下页 返回 结束 一、引例 1. 曲边梯形的面积 设曲边梯形是由连续曲线 y  f (x) ( f (x)  0) 及 x轴，以及两直线 x  a, x  b 所围成 , 求其面积 A . A  ? y  f (x) 矩形面积 a h  a h a h 梯形面积 ( ) b 2 a b h   y O a b x

解决步骤： 1)分割.在区间[a,b]中任意插入n-1个分点 a=x0<x<x2<<Xn-1<xn=b 用直线x=x,将曲边梯形分成个小曲边梯形： 2)近似代替.在第i个窄曲边梯形上任取5，∈[x-1,x] 作以[x1,x,]为底，f(5) 为高的小矩形。并以此小 矩形面积近似代替相应 窄曲边梯形面积△4，得 a xy Xi-1 xi bx 51 △4，≈f(5a)△x;(△x,=x1-xi-1,i=1,2,…,n) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束

目录 上页 下页 返回 结束 1x i x i1 a x b x y O 解决步骤 : 1) 分割. 在区间 [a , b] 中任意插入 n –1 个分点 a x x x x x b  0  1  2  n1  n  [ , ] i i 1 i x x    用直线 i x  x 将曲边梯形分成 n 个小曲边梯形; 2) 近似代替. 在第i 个窄曲边梯形上任取 作以[ , ] i 1 i x x  为底 , ( ) i f  为高的小矩形, 并以此小 矩形面积近似代替相应 窄曲边梯形面积 , Ai 得 ( ) ( )  i  i  i  i  i  i1 A f  x x x x , i 1,2,,n )  i

3)求和. A=2A4,=2f5)△x i=1 i=1 4)取极限.令2=max{△x},则曲边梯形面积 1si≤n n A=lim∑A4, 2→0 1 lim∑f(5,)△x, 0 a O a x Xi-xi bx BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束

目录 上页 下页 返回 结束 3) 求和.     n i A Ai 1     n i i i f x 1 ( ) 4) 取极限. 令 max{ }, 1 i i n  x    则曲边梯形面积      n i A Ai 1 0 lim       n i i i f x 1 0 lim ( )  1x i x i1 a x b x y O  i

2.变速直线运动的路程 设某物体作直线运动，己知速度v=v(t)∈C[T,T],且 v(t)≥0，求在运动时间内物体所经过的路程s. 解决步骤： 1)分割.在[☑，T]中任意插入n-1个分点，将它分成 n个小段[t-1,t](i=1,2,…,n),在每个小段上物体经 过的路程为△S,(i=1,2,…,n) 2)近似代替.任取5，∈[，-1,1]，以v(x,)代替变速，得 △S,≈v(t,)△t,(i=1,2,…,n) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束

目录 上页 下页 返回 结束 2. 变速直线运动的路程 设某物体作直线运动, ( ) [ , ], C T1 T2 v  v t  且 v(t)  0, 求在运动时间内物体所经过的路程 s. 解决步骤: 1) 分割. [ , ], i i 1 i t t 任取   将它分成 [ , ]( 1, 2, , ), 1 t t i n i i   在每个小段上物体经 2) 近似代替. 以 ( )代替变速 , i v  得 i i i  s  v( )t [ , ] 1 , 在 T1 T2 中任意插入 n  个分点 s (i 1, 2, , n)  i   (i 1, 2,,n) 已知速度 n 个小段 过的路程为

3)求和. s≈∑c,)A i 4)取极限. s =limv()At, (2=max△t,) 2→0 lsi≤n 上述两个问题的共性： ·解决问题的方法步骤相同 “分割，近似代替，求和，取极限” 。所求量极限结构式相同： 特殊乘积和式的极限 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束

目录 上页 下页 返回 结束 3) 求和. i n i i s  v t 1 ( ) 4) 取极限 . i n i i s  v t   1 0 lim ( )  ( max ) 1 i i n  t    上述两个问题的共性: • 解决问题的方法步骤相同 : “分割 , 近似代替 , 求和 , 取极限 ” • 所求量极限结构式相同: 特殊乘积和式的极限

二、定积分定义 定义设函数f(x)定义在[a,b]上，若对[a,b]的任一种分法 a=x0<为<x2<<xn=b,令△x;=x,-x1,任取 5,∈[x,1,x,],只要元=max{△x,}→0时∑f(5)△x, 1si≤n i=l 总趋于确定的极限I,则称此极限I为函数f(x)在区间 [a,b1上的定积分，记作心f(x)dx 即 心fx)dx=mΣ5，)， 2→01 此时称f(x)在[a,b]上可积 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束

目录 上页 下页 返回 结束 O a b x 二、定积分定义 定义 设函数 f (x)定义在[a,b]上, 若对[a, b]的任一种分法 , 0 1 2 a x x x x b     n  ,  i  i  i1 令 x x x 任取 [ , ] , i i 1 i x x     i 只要 max{ } 0时 1      i i n  x i n i i  f x 1 ( ) 总趋于确定的极限 I ,则称此极限 I 为函数 f (x) 在区间 [a, b]上的定积分, 1 x i x i1 x  b a f (x)dx 即   b a f (x)dx i n i i  f x  1 0 lim ( )  此时称 f ( x ) 在 [ a , b ] 上可积 . 记作

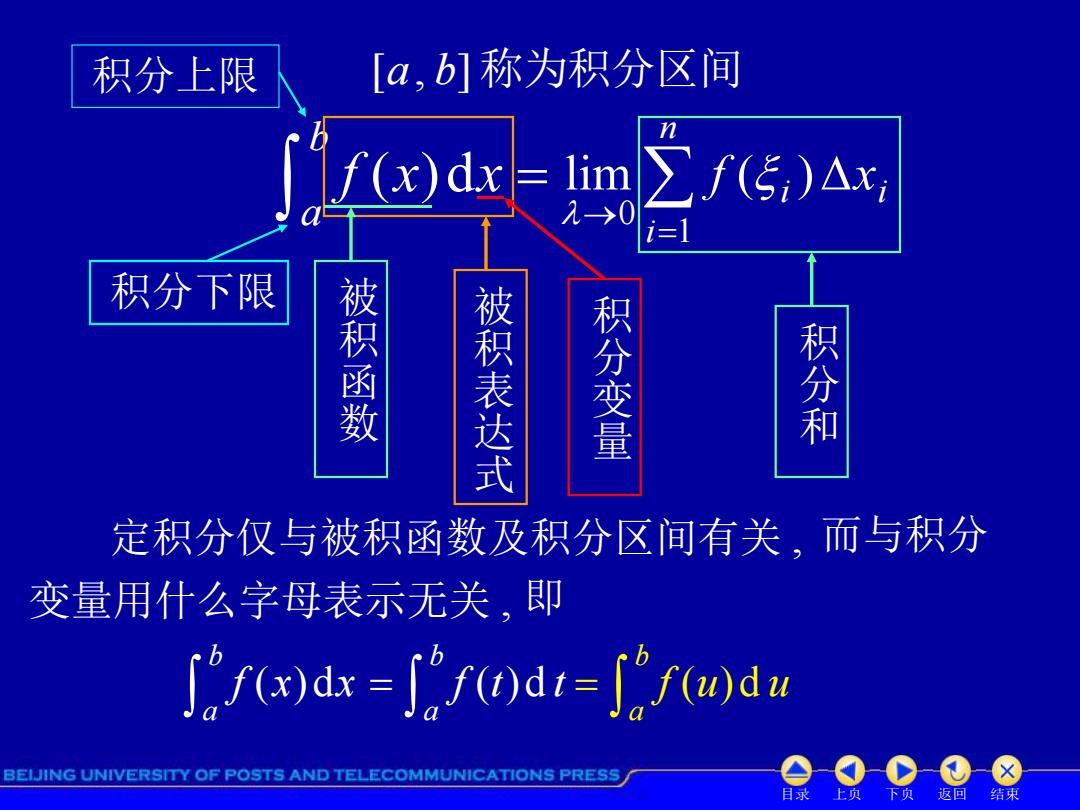
积分上限 [a,b]称为积分区间 f网 f(5,)Ax i=1 积分下限 被积函数 被积表达式 积分变量 积分和 定积分仅与被积函数及积分区间有关，而与积分 变量用什么字母表示无关，即 dx-at-d BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 录 返回 结束

目录 上页 下页 返回 结束   b a f (x)dx i n i i  f x   1 0 lim ( )  积分上限 积分下限 被 积 函 数 被 积 表 达 式 积 分 变 量 积 分 和 [a, b] 称为积分区间 定积分仅与被积函数及积分区间有关 , 而与积分 变量用什么字母表示无关 , 即  b a f (x)dx   b a f (t)d t   b a f (u)d u

可积的充分条件： 定理1函数f(x)在[a,b]上连续>f(x)在[a,b]可积. 定理2函数f(x)在[a,b]上有界，且只有有限个间断点 →f(x)在[a,b]可积 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页 返回 结束

目录 上页 下页 返回 结束 可积的充分条件: 定理1 函数 f (x)在[a,b]上连续 f (x)在 [a,b]可积. 定理2 函数 f (x)在[a,b]上有界, 且只有有限个间断点 f (x)在 [a,b]可积