
第4节 第九章 对面积的曲面积分 一 对面积的曲面积分的概念与性质 二、对面积的曲面积分的算法 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 第4节 一、对面积的曲面积分的概念与性质 二、对面积的曲面积分的算法 对面积的曲面积分 第九章

一、对面积的曲面积分的概念与性质 1.引例:设曲面形构件具有连续面密度4(x,y,z),求质 量M 类似求平面薄板质量的思想,采用 (5,7,5) 分割,近似,求和,取极限 的方法,可得 M=1im∑4(5,7,5,)△S 20 其中,λ表示n小块曲面的直径的 最大值(曲面的直径为其上任意两点间距离的最大者) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 O x y z 一、对面积的曲面积分的概念与性质 1.引例: 设曲面形构件具有连续面密度 类似求平面薄板质量的思想, 采用 可得 1 ( , , ) n i i i i i S = M = ( , , ) i i i 求质 “分割, 近似, 求和, 取极限” 的方法, 量 M. 其中, 表示 n 小块曲面的直径的 最大值 (曲面的直径为其上任意两点间距离的最大者)

2对面积的曲面积分的定义 定义:设∑为光滑曲面,f(x,y)是定义在∑上的 有界函数, 若对Σ做任意分割和局部区域任意取点 乘积和式极限 (5)AS 记作 f(x,y,=)ds 都存在,则称此极限为函数f(x,y)在曲面Σ上对面积 的曲面积分或第一类曲面积分.其中f(x,yz)叫做被积 函数,∑叫做积分曲面 据此定义,曲面形构件的质量为M=小4(x,y,)dS 曲面面积为S=厂2ds BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 M x y z S ( , , )d = 定义: 设 为光滑曲面, “乘积和式极限” 都存在, 的曲面积分 f (x, y,z)d S 其中 f (x, y, z) 叫做被积 据此定义, 曲面形构件的质量为 曲面面积为 f (x, y, z) 是定义在 上的 有界函数, 记作 或第一类曲面积分. 若对 做任意分割和局部区域任意取点, 则称此极限为函数 f (x, y, z) 在曲面 上对面积 函数, 叫做积分曲面. 2.对面积的曲面积分的定义

3对面积的曲面积分的性质 (1)线性性质 [(x,,)+ng(x,y,)]dS =kf()dS+)dS; (2)分域性质 若∑是分片光滑的,例如分成两 片光滑曲面马,∑2,则有 ∬2fx,yads=八fx,)as+,ca)ds BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 kf x y z hg x y z S ( , , ) ( , , ) d + (1)线性性质 k f x y z S h g x y z S ( , , )d ( , , )d ; = + 3.对面积的曲面积分的性质 (2)分域性质 , , 1 2 则有 = f (x, y,z)d S 1 ( , , )d f x y z S 若 是分片光滑的, 例如分成两 片光滑曲面
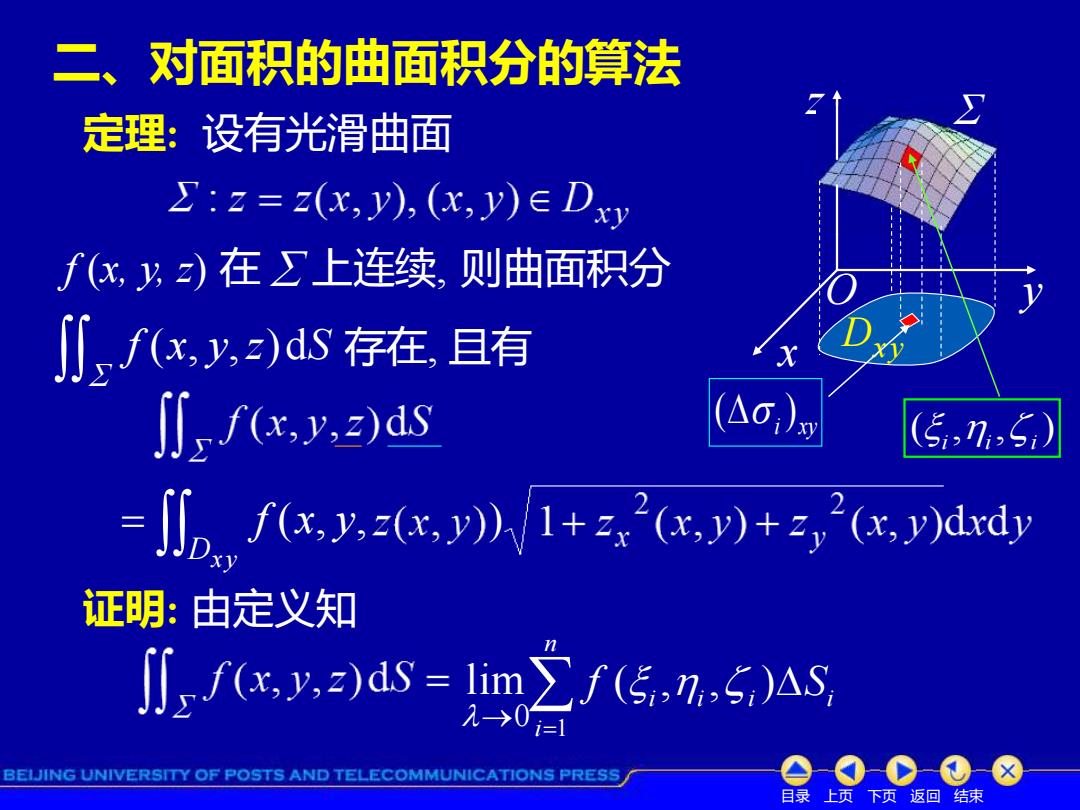
二、对面积的曲面积分的算法 定理:设有光滑曲面 ∑:z=z(x,y),(x,y)∈Dxy f(,y)在∑上连续,则曲面积分 ∬2f(x,y,)ds存在且有 ∬2f(x,y,2)ds (5,7,5) -)j1+zG.y)+z,(w.ydxdy 证明:由定义知 ∬2f(x,y,2dS=1im∑f(5,n,5)AS BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 O x y z 定理: 设有光滑曲面 f (x, y, z) 在 上连续, 存在, 且有 f (x, y,z)dS = Dx y f (x, y, ) 二、对面积的曲面积分的算法 则曲面积分 证明: 由定义知 1 ( , , ) n i i i i i f S = 0 lim → Dxy ( , , ) i i i ( ) i xy

而△S,=V+6xt,(,)ddy =√1+二,(n0+,2(50(△a), 小fx,,2)ds 1im∑f(5,7,z5,7》 2-→0同 V1+250+,(50(△o,), =1imΣf(5,n,2(5,n,》 ②光滑) 0 V1+2(5,7)+,(5,7)(△a,)y .)dxdy BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 2 2 ( ) 1 ( , ) ( , ) d d i x y x y z x y z x y x y + + 2 2 1 ( , ) ( , ) ( ) x i i y i i i x y = + + z z 2 2 1 ( , ) ( , ) ( ) x i i y i i i x y + + z z 2 2 1 ( , ) ( , ) ( ) x i i y i i i x y + + z z f x y z x y z x y x y x y Dx y ( , , ) 1 ( , ) ( , )d d 2 2 = + + f (x, y,z)dS 而 ( 光滑)

说明: 1)如果曲面方程为 x=x(y,z),(y,2)∈DyE 或y=Jy(x,),(x,)∈Dxz 可有类似的公式 2)若曲面为参数方程,只要求出在参数意义下dS 的表达式,也可将对面积的曲面积分转化为对参数的 二重积分 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 说明: Dyz x = x( y,z), ( y,z) Dxz 或 y = y(x,z), (x,z) 可有类似的公式. 1) 如果曲面方程为 2) 若曲面为参数方程, 只要求出在参数意义下dS 的表达式 , 也可将对面积的曲面积分转化为对参数的 二重积分

刚,41计算曲面积盼八, 其中Σ是球面x2+y2+2 =a被平面z=h(0<h<a截出的顶部. 解:z=√a2-x2-y2,(x,)eDy Dyx2+y2≤a2-h2 1++5=。--y -a3,a0ae7 adxdy a2-x2 -2x4-a。-y] 2-h2 =2πan BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 Dxy 例9.4.1 计算曲面积分 其中 是球面 被平面 截出的顶部. 解: 2 2 2 2 Dxy : x + y a − h 2 2 1 x y + z + z z d S = 2π 0 a d 2 2 1 2 2 2 π ln( ) 2 0 a h a a r − = − − − − = Dx y a x y a x y 2 2 2 d d − − 2 2 0 2 2 a h d a r r r x z y h a

思考: 若∑是球面x2+y2+z2=a2被平行平面z=±h截 出的上下两部分,则 0 h j儿e4an台 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 思考: 若 是球面 被平行平面 z =±h 截 出的上下两部分, ( ) d = z S ( ) d = z S 0 4 ln π h a a 则 h − h x z y

例.4.4计算厂,xyzdS,其中Σ是由平面x+y+z=1与 坐标面所围成的四面体的整个边界曲面! 解:设1,卫2,3,卫4分别表示∑在平面 x=0,y=0,z=0,x+y+z=1上的部分,则 原式= +,+,as -xds 5=1--D,06 -3xx月0-x-d=i20 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例9.4.4 计算 其中 是由平面 坐标面所围成的四面体的整个边界曲面. 解: 设 上的部分, 则 1 2 3 4 , , , = 4 d xyz S : 1 , 4 z = − x − y − 0 1 0 1 ( , ) : x y x x y Dxy − − − x y x y y 1 0 (1 ) d 120 3 = 与 = 1 0 3 x dx + + + 1 2 3 4 xyz dS 原式 = 分别表示 在平面 z y x 1 1 1