
第一章 行列式 目录 四1.1二阶和三阶行列式 四1.2n阶行列式 ★1.3行列式的性质 四1.4行列式的计算 四1.5克拉默法则 河套大学《线性代数》课件 快乐学司
第一章 行列式 1.1 二阶和三阶行列式 1.2 阶行列式 ★ 1.3 行列式的性质 1.4 行列式的计算 1.5 克拉默法则 n 目录 河套大学《线性代数》课件 快乐学习
存节授裸计划 水人 (2课时) 尚本 必新课 1.3行列式的性质 第四次课 必小结 》思考题及答案提示 必练习、作业及参考答案 河套大学《线性代数》课件 第一章行列式 快东学可
快乐学习 以人 为本 河套大学《线性代数》课件 ❖新课 1.3 行列式的性质 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 四 次 课 本节授课计划(2课时) 第一章 行列式

水人 1.3行列式的性质 尚本 主题调 1.行列式的初等变换 2.行列式的转置 3.行列式基本性质 4.下三角行列式 5.行列式性质 返回 河套大学《线性代数》课件 第一章行列式 快东学司
快乐学习 以人 为本 河套大学《线性代数》课件 主 题 词 1.3 行列式的性质 1.行列式的初等变换 2.行列式的转置 3.行列式基本性质 4.下三角行列式 5.行列式性质 第一章 行列式 返回
相关内容回预 水人 尚本 定 n阶行列式等于它的某一行 行刻式的 义 或某一列每个元素与它的代 汁方法 法 数余子式乘积之和。 行列式的 选择有最多零的行或列展开 计算技巧 行列式是教的又一种特殊的表示方法 河套大学《线性代数》课件 第一章行列式 快东学司
快乐学习 以人 为本 河套大学《线性代数》课件 相关内容回顾 行列式的 计算方法 定 义 法 阶行列式等于它的某一行 或某一列每个元素与它的代 数余子式乘积之和。 n 行列式的 计算技巧 选择有最多零的行或列展开 行列式是数的又一种特殊的表示方法 第一章 行列式
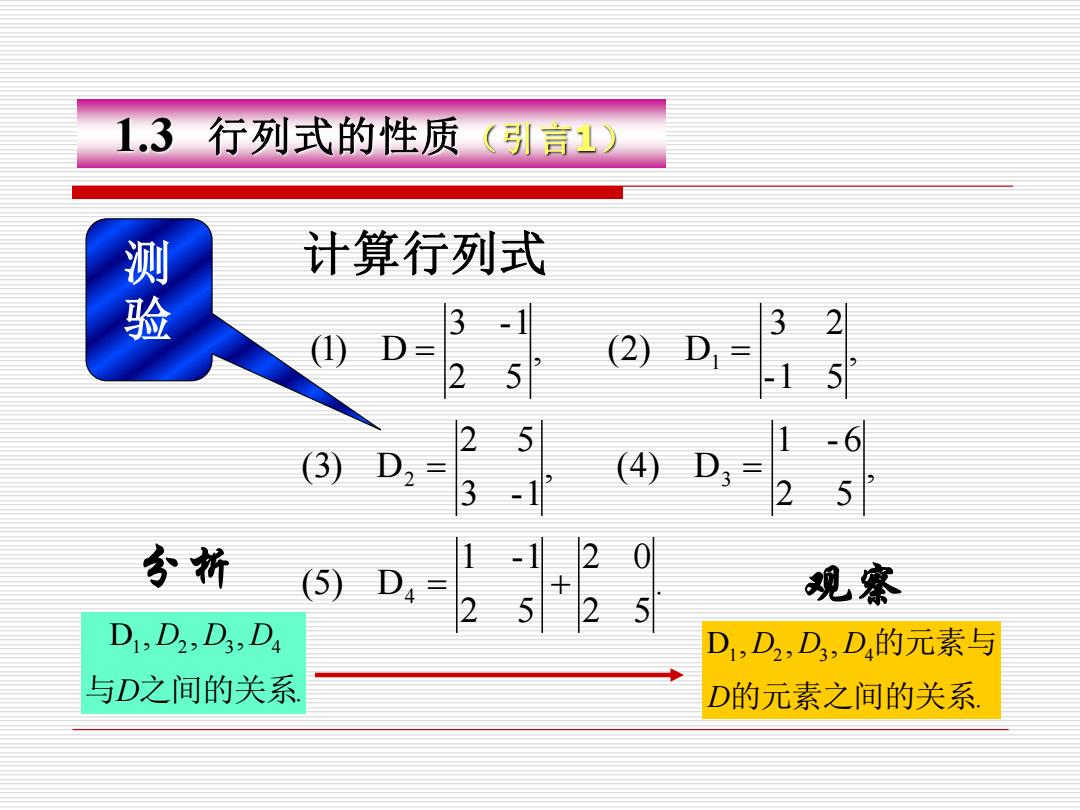
1.3行列式的性质(引言1) 测验 计算行列式 (2) 2 (4) 分折 (5) 观察 D1,D2,D3,D4 D1,D2,D3,D的元素与 与D之间的关系 D的元素之间的关系
1.3 行列式的性质(引言1) , 2 5 3 -1 (1) D = 计算行列式 , 3 -1 2 5 (3) D2 = , -1 5 3 2 (2) D1 = , 2 5 1 - 6 (4) D3 = . 2 5 2 0 2 5 1 -1 (5) D4 = + 测 验 分析 . D , , , 1 2 3 4 与D之间的关系 D D D 观察 . D , , , 1 2 3 4 的元素之间的关系 的元素与 D D D D

水人 1.3行列式的性质(引言2) 尚本 行列式的奥妙在于对行列式的行或列进行了 某些变换(如交换两行(列)位置、某行(列) 乘以某个数、某行(列)乘以某个数后加到另 行(列)等)后,行列式虽然会发生相应的变化, 但变换前后两个行列式却仍保持着某种关系,这 意味着我们可以利用这些关系简化高阶行列式的 计算.为了行列式计算的方便,我们引进行列式的 初等变换概念 河套大学《线性代数》课件 第一章行列式 快东学日
快乐学习 以人 为本 河套大学《线性代数》课件 1.3 行列式的性质(引言2) 计算.为了行列式计算的方便,我们引进行列式的 行列式的奥妙在于对行列式的行或列进行了 某些变换(如交换两行(列)位置、某行(列) 乘以某个数、某行(列)乘以某个数后加到另一 行(列)等)后,行列式虽然会发生相应的变化, 但变换前后两个行列式却仍保持着某种关系,这 意味着我们可以利用这些关系简化高阶行列式的 初等变换 概念. 第一章 行列式

水人 1.3行列式的性质(续1) 尚本 定义13.1行列式的初等行变换是指: ()用一个非零常数k遍乘行列式的某一行; (2)互换行列式任意两行的位置, (3)将行列式某一行加上另一行的k倍 将定义1.3.1中的“行”换成“列”,即得 行列式的初等列变换的定义 行列式的初等行变换与初等列变换统称为行 列式的初等变换 河套大学《线性代数》课件 第一章行列式 快乐骨司
定义1.3.1 行列式的初等行变换 是指: (1)用一个非零常数 遍乘 行列式的某一行; (2) 互换行列式任意两行的位置; (3) 将行列式某一行加上另一行的 倍. 快乐学习 以人 为本 河套大学《线性代数》课件 1.3 行列式的性质(续1) k 将定义1.3.1中的“行”换成“列”,即得 行列式的初等列变换 的定义. 列式的初等变换. 行列式的初等行变换与初等列变换统称为行 第一章 行列式 k

水人 1.3行列式的性质 (续2) 尚本 此外,行列式的计算是一个重要的问题,但 根据行列式的定义,计算一个n阶行列式,当n 比较大时,计算量很大,因此有必要讨论行列式 的其它计算方法 由上节给出的几个例题可以看出,在行列式的 计算过程中,为了计算简便,可选择含零元素较 多的一行(列)展开.本节将介绍行列式的性质, 利用这些性质可以将一个行列式中某行(列)的元 素尽可能多的化为零,以使行列式的计算变得简单, 河套大学《线性代数》课件 第一章行列式 快东学日
快乐学习 以人 为本 河套大学《线性代数》课件 1.3 行列式的性质(续2) n n 此外,行列式的计算是一个重要的问题,但 根据行列式的定义,计算一个 阶行列式,当 的其它计算方法. 比较大时,计算量很大,因此有必要讨论行列式 由上节给出的几个例题可以看出,在行列式的 计算过程中 ,为了计算简便,可选择含零元素较 多的一行(列)展开. 本节将介绍行列式的性质, 利用这些性质可以将一个行列式中某行(列)的元 素尽可能多的化为零,以使行列式的计算变得简单. 第一章 行列式

水人 1.3行列式的性质(续3 尚本 设n阶行列式 12 D C 02 020 将行列式D的相应的行变为相应的列, 得到的新行列式 d21 d 2 022 a2n 称为行列式D的转置行列式,记作 D 河套大学《线性代数》课件 第一章行列式 快东学司
的相应的行变为相应的列, 称为行列式 快乐学习 以人 为本 河套大学《线性代数》课件 1.3 行列式的性质(续3) n , 1 2 21 22 2 11 12 1 n n n n n n a a a a a a a a a D = D , 1 2 12 22 2 11 21 1 n n nn n n a a a a a a a a a . T D 设 将行列式 的转置行列式,记作 阶行列式 得到的新 行列式 第一章 行列式 D

人人 1.3行列式的性质(续4) 尚本 行列式基本性质: 行列 式 D与它的转置行列式D「相等 下面仅对三阶行列式作验证 若 ari d12 a3 C d21 D 1 a22 d23 D 12 d32 则 D=D d32 033 13 d33 河套大学《线性代数》课件 第一章行列式 快乐骨司
与它的转置行列式 快乐学习 以人 为本 河套大学《线性代数》课件 1.3 行列式的性质(续4) 下面仅对三阶行列式作验证. , 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = , 13 23 33 12 22 32 11 21 31 T a a a a a a a a a D = . T 则 D = D 第一章 行列式 D T D 行列式基本性质: 相等. 行列 式 若