
第二章 矩阵 目录 四 2.1 矩阵的概念 ★2.2 矩阵的运算 四 2.3 逆矩阵 四 2.4 矩阵的分块 四 2.5 初等变换与初等矩阵 四 2.6 矩阵的秩 四 2.7 应用举例 河套大学《线性代数》课件 第二章矩阵 快乐学司
第二章 矩 阵 2.1 矩阵的概念 ★ 2.2 矩阵的运算 2.3 逆矩阵 2.4 矩阵的分块 2.5 初等变换与初等矩阵 2.6 矩阵的秩 2.7 应用举例 目录 河套大学《线性代数》课件 第二章 矩阵 快乐学习
本节授裸计划 水人 (2课时) 尚本 &新课 ,2.2 矩阵的运算 第九次课 2.2.2 矩阵的乘法 小结 心思考题及答案提示 练习、1 作业及参考答案 河套大学《线性代数》课件 第二章矩阵 快东学可
快乐学习 以人 为本 ❖新课 2.2 矩阵的运算 2.2.2 矩阵的乘法 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 九 次 课 本节授课计划(2课时) 河套大学《线性代数》课件 第二章 矩阵

水人 2.2矩阵的运算《续) 尚本 主题调 1.一重求和符号 2,双重求和符号 3矩阵的乘法 4交换律 5.消去律 返回 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 为本 主 题 词 1.一重求和符号 2.双重求和符号 3.矩阵的乘法 4.交换律 5.消去律 1 2.2 矩阵的运算(续) 返回 河套大学《线性代数》课件 第二章 矩阵

水人 2.2.2矩阵的乘法 尚本 在作矩阵的乘法时,用求和符号比较方便,为此 在这里先作心点说明. 一重求和符号是我们所熟悉的,我们只指出以 下等式成立 ab.=h a=ha i=1 i=1 引入符号 这里的a与无关 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 2.2.2 矩阵的乘法 为本 在作矩阵的乘法时,用求和符号比较方便,为此 在这里先作几点说明. 一重求和符号 是我们所熟悉的,我们只指出以 下等式成立: = = = n i i n i a bi ab 1 1 = = = = n i i n i bi a b a 1 1 这里的 a 与 i 无关. 引入符号 河套大学《线性代数》课件 第二章 矩阵

以人 2.2.2矩阵的乘法 (续1) 尚本 我们要用到形如 ∑∑a,b,的双重求和符号. i=1j=1 双重求和符号的意思是,先对第二个求和符号 求和,再对第一个求和符号求和.则有, 2艺62a++ =1=1 i=1 =ab+ab2+…+ab,n+ +ab+ab2+…+a2bn+ 引入符号 土 +anb+anb2+…+anbn 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.2.2 矩阵的乘法 (续1) 为本 = = m i n j ai bj 1 1 我们要用到形如 双重求和符号的意思是,先对第二个求和符号 求和,再对第一个求和符号求和 . 则有, 的双重求和符号 . = = = = = m i n j n i n j ai bj ai bj 1 1 1 1 ( ) 1 2 1 n m i = ai b + b + + b = . 1 2 2 1 2 2 2 1 1 1 2 1 m m m n n n a b a b a b a b a b a b a b a b a b + + + + + + + + + + + = + + + + 引入符号 河套大学《线性代数》课件 第二章 矩阵

水人 2.2.2 矩阵的乘法(续2) 尚本 若交换求和符号的次序,则有 22a6,2a2(a+a,++a.b =1 =a,b,+a,b,+…+amb n m +ab2+a4,b2+…+anb ∑∑a,b,=∑∑ab i=1 i=l i=1 i=l +abn+abn+…+anb, 这两个等式的右端显然相等,因此有这就是 说,双重求和符号可以交换次序 引入符号 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 2.2.2 矩阵的乘法 (续2) 为本 若交换求和符号的次序,则有 j n j m i n j m i ai bj ai b = = = = = 1 1 1 1 = = + + + n j a a am bj 1 1 2 ( ) . 1 2 1 2 2 2 2 1 1 2 1 1 n n m n m m a b a b a b a b a b a b a b a b a b + + + + + + + + + = + + + 这两个等式的右端显然相等,因此有这就是 说,双重求和符号可以交换次序. = = = = = n j m i i j m i n j ai bj a b 1 1 1 1 . 引入符号 河套大学《线性代数》课件 第二章 矩阵

以人 2.2.2 矩阵的乘法(续3) 尚本 例2.2.5 某校明后两年计划建筑教学楼与宿舍 楼建筑面积及材料耗用量列表如下: 建筑面积(单位:100m2) 建筑 时间 面积 教学楼 宿舍楼 明年 20 10 后年 30 20 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.2.2 矩阵的乘法 (续3) 为本 例2.2.5 某校明后两年计划建筑教学楼与宿舍 楼.建筑面积及材料耗用量列表如下: 建筑面积(单位:100 ) 2 m 建筑 时间 面积 教学楼 宿舍楼 明年 20 10 后年 30 20 河套大学《线性代数》课件 第二章 矩阵
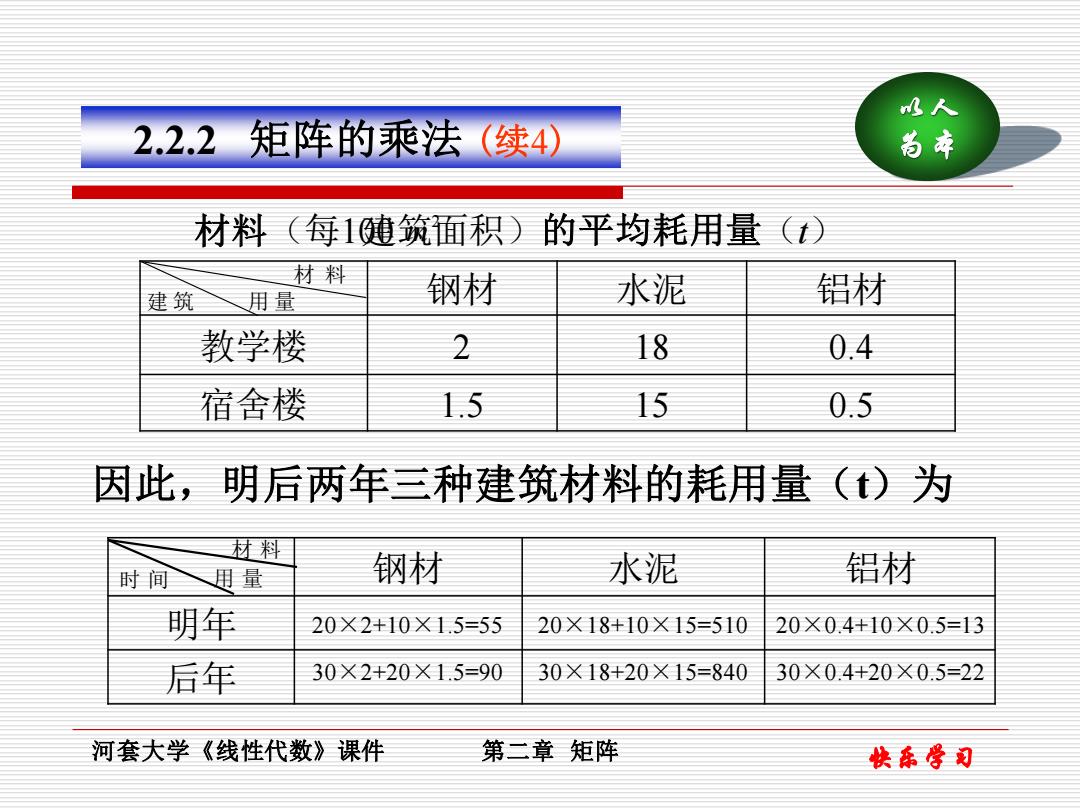
水人 2.2.2矩阵的乘法(续4) 尚本 材料(每1健筑面积)的平均耗用量() 材料 建筑 用量 钢材 水泥 铝材 教学楼 2 18 0.4 宿舍楼 1.5 15 0.5 因此,明后两年三种建筑材料的耗用量()为 材料 时间 思量 钢材 水泥 铝材 明年 20×2+10×1.5=55 20×18+10×15=510 20×0.4+10×0.5=13 后年 30×2+20X1.5=90 30×18+20×15=840 30×0.4+20×0.5=22 河套大学《线性代数》课件 第二章矩阵 快乐学司
建筑面积) m 2 的平均耗用量(t) 材 料 建 筑 用 量 材料(每100 钢材 水泥 铝材 教学楼 2 18 0.4 宿舍楼 1.5 15 0.5 因此,明后两年三种建筑材料的耗用量(t)为 钢材 水泥 铝材 明年 20×2+10×1.5=55 20×18+10×15=510 20×0.4+10×0.5=13 后年 30×2+20×1.5=90 30×18+20×15=840 30×0.4+20×0.5=22 材 料 时 间 用 量 以人 2.2.2 矩阵的乘法 (续4) 为本 河套大学《线性代数》课件 第二章 矩阵 快乐学习

水人 2.2.2矩阵的乘法 (续5) 尚本 若把上述三个数表用矩阵表示为: 2010 2 180.4 A= B= 3020 1.5150.5 20×2+10×1.5 20x18+10×15 20×0.4+10×0.5 C= 30×2+20×1.5 30×18+20×15 30×0.4+20×0.5 则矩阵C称为矩阵A与B的乘积 问数:矩阵C与A、B 奔 芳 元素之间有什么关系? 河套大学《线性代数》课件 第二章矩阵 快东学司
以人 2.2.2 矩阵的乘法 (续5) 为本 若把上述三个数表用矩阵表示为: , 30 20 20 10 A = , 0.5 0.4 15 18 1.5 2 B = 则矩阵 C 称为矩阵 A 与 B 的乘积. , 30 0.4 20 0.5 20 0.4 10 0.5 30 18 20 15 20 18 10 15 30 2 20 1.5 20 2 10 1.5 + + + + + + C = 问题:矩阵 C 与 A、B 元素之间有什么关系? 河套大学《线性代数》课件 第二章 矩阵 快乐学习

水人 2.2.2矩阵的乘法(续6) 尚本 例2.2.6设有两个线性变换 21=ay+4122 (2.2.1) 22=421y1+022y2, 23=031y1+0322 y=bx+b12x2, y2=b11+b23 (2.2.2) 若需求出由X,x2到☑,22,23的线性变换,可将 (2.2.2)代入(2.2.10,得 河套大学《线性代数》课件 第二章矩阵 快东骨司
以人 2.2.2 矩阵的乘法 (续6) 为本 例2.2.6 设有两个线性变换 = + = + = + . , , 3 31 1 32 2 2 21 1 22 2 1 11 1 12 2 z a y a y z a y a y z a y a y = + = + . , 2 21 1 22 2 1 11 1 12 2 y b x b x y b x b x (2.2.1) (2.2.2) 1 2 x , x 1 2 3 若需求出由 到 z ,z ,z 的线性变换,可将 (2.2.2)代入(2.2.1),得 河套大学《线性代数》课件 第二章 矩阵 快乐学习