
第一章 行列式 目录 四1.1二阶和三阶行列式 ★1.2n阶行列式 四1.3行列式的性质 四1.4行列式的计算 四1.5克拉默法贝则 河套大学《线性代数》课件 快乐学司
第一章 行列式 1.1 二阶和三阶行列式 ★ 1.2 阶行列式 1.3 行列式的性质 1.4 行列式的计算 1.5 克拉默法则 n 目录 河套大学《线性代数》课件 快乐学习
存节授裸计划 水人 (2课时) 尚本 必新课 1.2 n阶行列式 1.2.1n阶行列式的定义 第三次课 1.2.2n阶行列式展开定理 小结 》思考题及答案提示 必练习、作业及参考答案 河套大学《线性代数》课件 快乐学司
快乐学习 以人 为本 河套大学《线性代数》课件 ❖新课 1.2 阶行列式 1.2.1 阶行列式的定义 1.2.2 阶行列式展开定理 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 三 次 课 本节授课计划(2课时) n n n
水人 1.2 n阶行列式 尚本 主题调 1.n阶行列式 2.余子式 3.代数余子式 4.行列式展开定理 5,对角行列式 6.上三角行列式 返回 河套大学《线性代数》课件 第一章行列式 快东学司
1. 阶行列式 2.余子式 3.代数余子式 4.行列式展开定理 5.对角行列式 6.上三角行列式 快乐学习 以人 为本 河套大学《线性代数》课件 主 题 词 1.2 n 阶行列式 第一章 行列式n 返回

相关内容回预 水人 尚本 二阶行列式等于它的第一行每个元素与它 的代数余子式乘积之和;三阶行列式等于它的第 一行每个元素与它的代数余子式乘积之和. 二阶 D=aAu+a2 A2> 三阶 D=auAu+an An2+aA 精测:n阶行列式等于它的第一行每个元素与 它的代数余子式乘积之和 河套大学《线性代数》课件 第一章行列式 快乐骨司
二阶行列式等于它的第一行每个元素与它 的代数余子式乘积之和;三阶行列式等于它的第 一行每个元素与它的代数余子式乘积之和. 快乐学习 以人 为本 河套大学《线性代数》课件 相关内容回顾 猜测: 阶行列式等于它的第一行每个元素与 它的代数余子式乘积之和 n 第一章 ? 行列式 , D a11A11 a12A12 a13A13 = + + , D a11A11 a12A12 二阶 = + 三阶
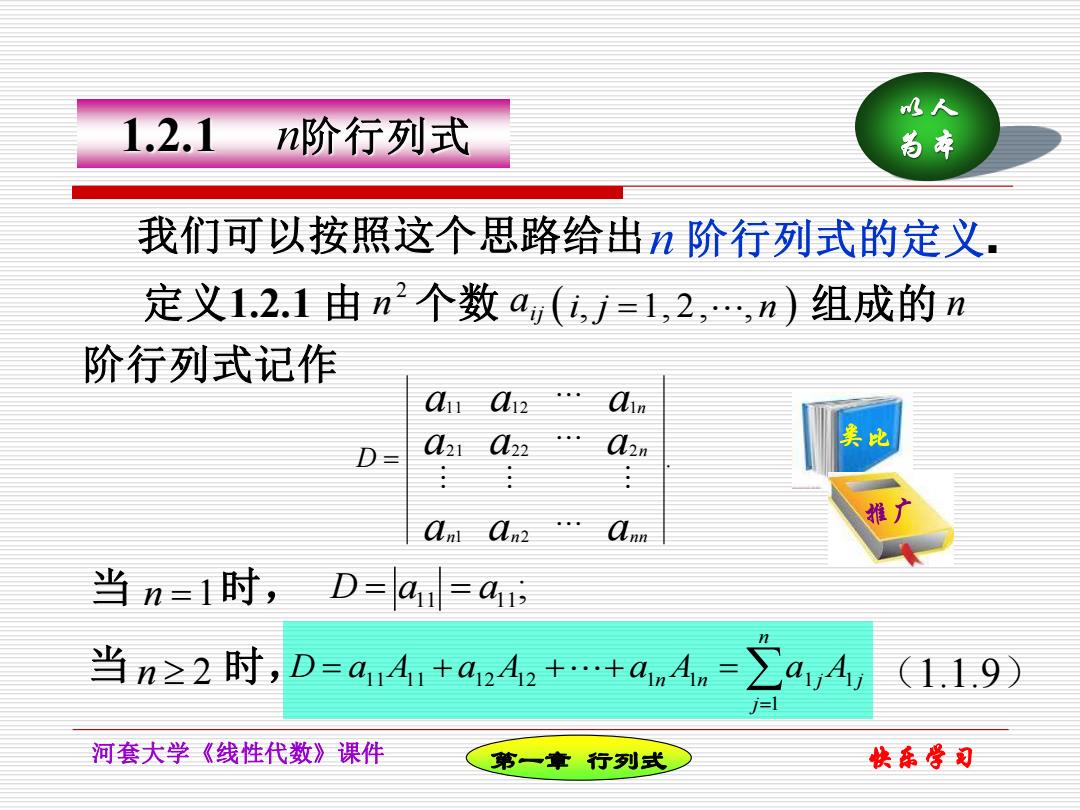
水人 1.2.1 n阶行列式 尚本 我们可以按照这个思路给出阶行列式的定义, 定义1.2.1由n2个数a(,j=1,2,,n)组成的n 阶行列式记作 ain 集比 D a21a22 a2n 推 an2 ann 当n=1时,Da =a 当n≥2时,D=a414,+a4,+…+an4n=∑4,4 (1.1.9) i= 河套大学《线性代数》课件 第一章行列式 快东学司
我们可以按照这个思路给出 快乐学习 以人 为本 河套大学《线性代数》课件 n 1.2.1 n 阶行列式 阶行列式的定义. n 2 定义1.2.1 由 n 个数 aij ( i, j =1, 2, , n ) 组成的 阶行列式记作 . 1 2 21 22 2 11 12 1 a a a a a a a a a n n n n n n D = n =1 n 2 = = + + + = n j D a A a A a n An a j A j 1 11 11 12 12 1 1 1 1 当 时, 当 时, (1.1.9) ; D = a11 = a11 第一章 行列式

水人 1.2.1 n阶行列式(续1) 尚本 其中A,为D的元素a,的代数余子式. 灌:对二、三阶行列式余子式写代数余子式的橇念进行推 广,可得阶行列式余子式乌代数余子式的橇念.(栋习) 数学思想 特殊到一般 例1.2.1应用行列式的定义计算四阶行列式 2 -2 3 D 0 2 0 河套大学《线性代数》课件 第一章行列式 快东学司
注:对二、三阶行列式余子式与代数余子式的概念进行推 广,可得 阶行列式余子式与代数余子式的概念.(练习) 快乐学习 以人 为本 河套大学《线性代数》课件 1.2.1 n 阶行列式(续1) 其中 A1 j 为 D 的元素 a1 j 的代数余子式. n 例1.2.1 应用行列式的定义计算四阶行列式. . 2 0 5 1 0 1 2 3 3 0 1 1 2 1 2 4 − − D = 数学思想 特殊到一般 第一章 行列式

水人 1.2.1 n阶行列式(续2) 尚本 解 0 311 D=2(123+(石 023+ 05 251 30 3 0 +(2(0-13+4 0-12 20 20 =2(5+1)-(6+6-4-45)-23+2)-415+2 =-8+37+2+52=83 问邀乏 是否可以按其它行或列展开? 徐习按第四行展开计算行列式。 河套大学《线性代数》课件 第一章行列式 快东学司
快乐学习 以人 为本 河套大学《线性代数》课件 1.2.1 n 阶行列式(续2) 解 ( ) ( ) ( )( ) ( ) ( ) ( ) ( ) ( ) 8 37 2 52 83. 2 5 1 6 6 4 45 2 3 2 4 15 2 2 0 5 0 1 2 3 0 1 4 1 2 0 1 0 1 3 3 0 1 2 1 2 5 1 0 2 3 3 1 1 1 1 0 5 1 1 2 3 0 1 1 2 1 1 3 1 4 1 1 1 2 = − + + + = = − + − + − − − − + − − + + − − − + − − = − − + − + + + + + D 问题: 是否可以按其它行或列展开? 第一章 行列式 练习:按第四行展开计算行列式

水人 1.2.2n阶行列式展开定理 尚本 椎广,与三阶行列式一样,n阶行列式也有类似的 行列式展开定理 定理1.1.2n阶行列式等于它的任一行或任一列 的每个元素与它的代数余子式的乘积之和,即 D=aAn±anA,+±anAn=∑a,A0=l2,s,m 或DQa,A,±a,A,++awA∑a,AG=,2,sm 河套大学《线性代数》课件 第一章行列式 快乐学司
快乐学习 以人 为本 河套大学《线性代数》课件 1.2.2 n 阶行列式展开定理 n n ... ( 1,2, , ). 1 1 1 2 2 D a A a A a A a A i n i j n j = i i + i i + + i n i n = i j = = ... ( 1,2, , ). 1 1 1 2 2 D a A a A a A a A j n i j n i = j j + j j + + n j n j = i j = = 与三阶行列式一样, 阶行列式也有类似的 阶行列式等于它的任一行或任一列 或 定理1.1.2 的每个元素与它的代数余子式的乘积之和,即 行列式展开定理. 第一章 行列式 推广:

水人 1.2.2n阶行列式展开定理(续1) 尚本 般来说,低阶行列式比高阶行列式的计 算要简单,根据上述定理,能够把n阶行列式 用-1阶行列式来表示,从而将高阶行列式的 计算问题转化为低阶行列式的计算. 化恒 n阶行列式 n-1阶行列式 转化与化归思想 河套大学《线性代数》课件 第一章行列式 快东学司
体会 1.2.2 阶行列式展开定理(续1) 一般来说,低阶行列式比高阶行列式的计 算要简单,根据上述定理,能够把 快乐学习 以人 为本 河套大学《线性代数》课件 n n n−1 阶行列式 计算问题转化为低阶行列式的计算. 用 阶行列式来表示,从而将高阶行列式的 n 阶行列式 化归 n −1 阶行列式 转化与化归思想 第一章 行列式
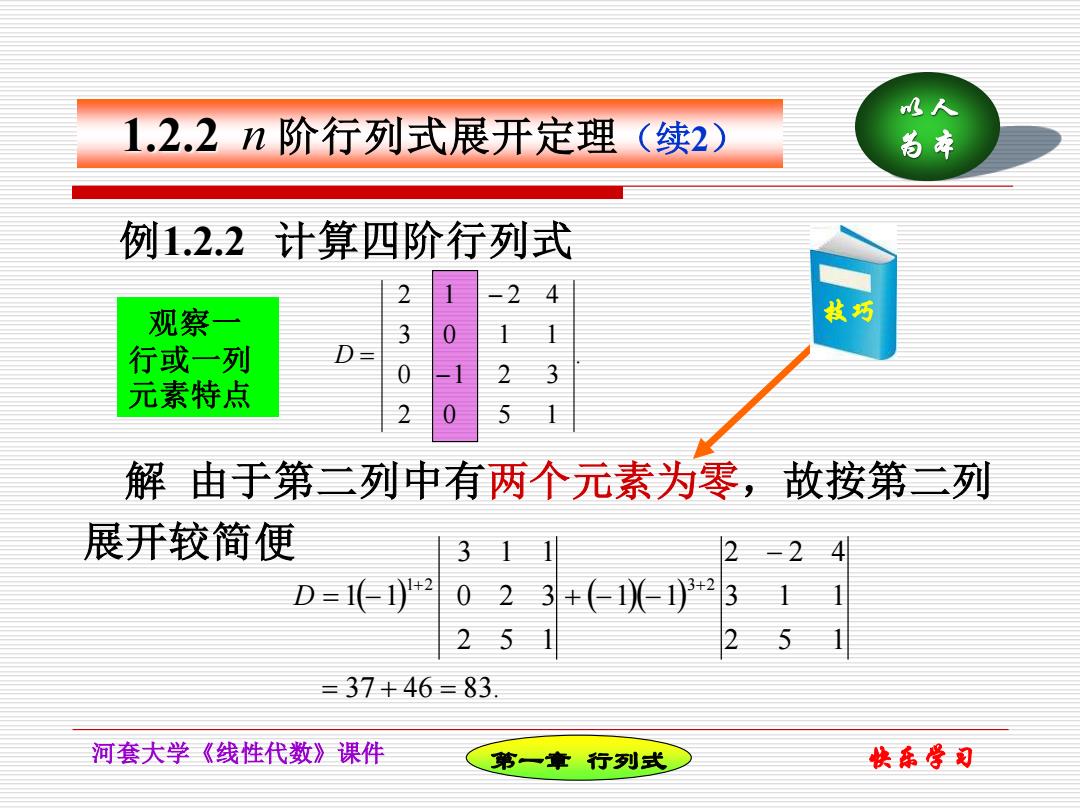
水人 1.2.2n阶行列式展开定理(续2) 尚本 例1.2.2计算四阶行列式 2 观察一 枝巧 3 行或一列 D 0 元素特点 2 0 解由于第二列中有两个元素为零,故按第二列 展开较简便 31 2-2 D=( 023 3 25 2 =37+46=83 河套大学《线性代数》课件 第一章行列式 快乐骨司
解 由于第二列中有两个元素为零,故按第二列 展开较简便 1.2.2 阶行列式展开定理(续2) 快乐学习 以人 为本 河套大学《线性代数》课件 n . 2 0 5 1 0 1 2 3 3 0 1 1 2 1 2 4 − − D = ( ) ( )( ) 37 46 83. 2 5 1 3 1 1 2 2 4 1 1 2 5 1 0 2 3 3 1 1 1 1 1 2 3 2 = + = − = − + − − + + D 例1.2.2 计算四阶行列式 技巧 第一章 行列式 观察一 行或一列 元素特点