
第二章 矩阵 目录 四 2.1 矩阵的概念 ★2.2 矩阵的运算 四 2.3 逆矩阵 四 2.4 矩阵的分块 四 2.5 初等变换与初等矩阵 四 2.6 矩阵的秩 四 2.7 应用举例 河套大学《线性代数》课件 第二章矩阵 快乐学司
第二章 矩 阵 2.1 矩阵的概念 ★ 2.2 矩阵的运算 2.3 逆矩阵 2.4 矩阵的分块 2.5 初等变换与初等矩阵 2.6 矩阵的秩 2.7 应用举例 目录 河套大学《线性代数》课件 第二章 矩阵 快乐学习

本节授裸计划 人人 (2课时) 尚本 必新课 2.2 矩阵的运算 第十次课 2.2.3 矩阵的转置 2.2.4方阵的行列式 必小结 》思考题及答案提示 必练习、作业及参考答案 河套大学《线性代数》课件 第二章矩阵 快乐学司
快乐学习 以人 为本 ❖新课 2.2 矩阵的运算 2.2.3 矩阵的转置 2.2.4 方阵的行列式 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 十 次 课 本节授课计划(2课时) 河套大学《线性代数》课件 第二章 矩阵

水人 2.2 矩阵的运算(续) 尚本 主题调 1,转置矩阵 2.对称矩阵 3,反对称矩阵 4.方阵的行列式 5.行列式乘法公式 6.伴随矩阵 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 为本 主 题 词 1 2.2 矩阵的运算(续) 1.转置矩阵 2.对称矩阵 3.反对称矩阵 4.方阵的行列式 5.行列式乘法公式 6.伴随矩阵 河套大学《线性代数》课件 第二章 矩阵

水人 2.2.3矩阵的转置 尚本 定义2.2.4设m×n矩阵 02 0 0h2 A= 09 行变成 则侧n×m矩阵 对应列 22 1112 中中中中中 称为mxn矩阵A的转置矩阵,简称A的转置, 河套大学《线性代数》课件 第二章矩阵 快乐学司
, .... .... .... 1 2 21 22 2 11 12 1 = m m mn n n a a a a a a a a a A n n mn m m a a a a a a a a a 1 2 12 22 2 11 21 1 快乐学习 以人 2.2.3 矩阵的转置 为本 定义2.2.4 设 mn 矩阵 则 nm 矩阵 称为 mn 矩阵 A 的转置矩阵,简称 A 的转置, 行变成 对应列 河套大学《线性代数》课件 第二章 矩阵
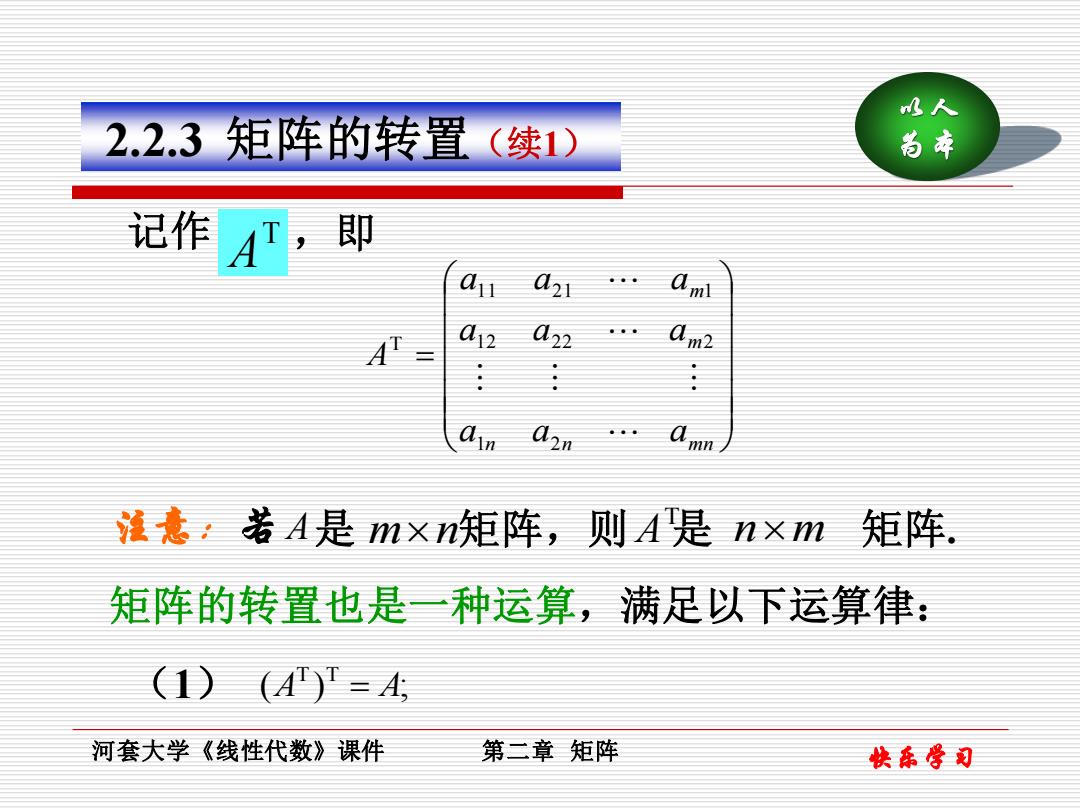
人人 2.2.3矩阵的转置(续1) 尚本 记作 AT即 a m a 2 l22 ”” a2n a m 滋意:若A是mxn矩阵,则A是 nx m 矩阵 矩阵的转置也是一种运算,满足以下运算律: (1)(A)=A 河套大学《线性代数》课件 第二章矩阵 快东骨司
快乐学习 以人 2.2.3 矩阵的转置(续1) 为本 T 记作 A ,即 = n n mn m m a a a a a a a a a A 1 2 12 22 2 11 21 1 T A mn T 注意:若 是 矩阵,则 A 是 nm 矩阵. 矩阵的转置也是一种运算,满足以下运算律: (1) ( ) ; T T A = A 河套大学《线性代数》课件 第二章 矩阵

水人 2.2.3矩阵的转置(续2) 尚本 (2)(A+B)I=A+B可推广为 (A+B++C=A+B++C雪 (3)(4④-4(为常数) (4)(AB)T=BA可推广为 (AB..C=BTAT...CT 下面只证明(4) 证明设A=(Q)ms,B=(色,)m,则(4B与B 都是nxm矩阵,而(AB)的第1行第)列的元素 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.2.3 矩阵的转置(续2) 为本 ( ) . T T T A+ B = A + B ( ) ; T T T T A+ B ++C = A + B ++C (2) 可推广为 (3) ( ) ( ) A T = A T 为常数 ; . T T T (AB) = B A T T T T (4) 可推广为 (ABC) = B A C . 下面只证明(4) A aij ms = ( ) ij sn B = (b ) T (AB) T T B A nm 证明 设 , ,则 与 都是 矩阵,而 T (AB) 的第 i 行第 j 列的元素 河套大学《线性代数》课件 第二章 矩阵
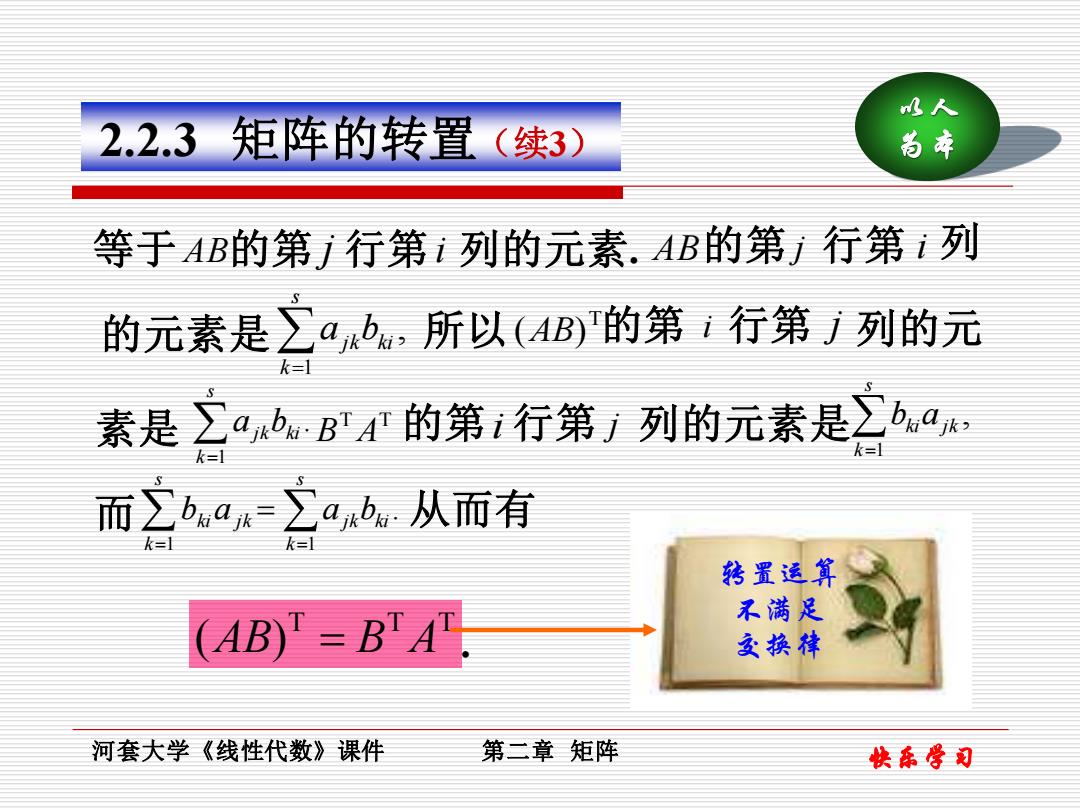
水人 2.2.3矩阵的转置(续3) 尚本 等于AB的第j行第ì列的元素.AB的第行第1列 的元素是∑4bu,所以(4B)的第i行第列的元 k三 素是∑abB'的第i行第/列的元素是∑ba, k=1 而》ba∑ab从而有 转置运算 (AB)T=BTAT 不满足 交换律 河套大学《线性代数》课件 第二章矩阵 快乐学司
快乐学习 以人 2.2.3 矩阵的转置(续3) 为本 AB 的第 j 行第 i 的元素是 , 1 = s k ajkbki T 所以 (AB) 第 i 行第 j 列的元 . 1 = s k ajkbki T T B A 的第 i 行第 j 列的元素是 , 1 = s k bkiajk 而 = s k bkia jk 1 . 1 = = s k ajkbki 从而有 T T T (AB) = B A 的 . 等于 AB 的第 j 行第 i 列的元素. 列 素是 转置运算 不满足 交换律 河套大学《线性代数》课件 第二章 矩阵

水人 2.2.3矩阵的转置(续4) 尚本 例2.2.11已知 A= 2 B= 4 求BA 解(方法一) 2 BTAT= 4 3 45 21628 111 19 河套大学《线性代数》课件 第二章矩阵 快乐学可
快乐学习 以人 2.2.3 矩阵的转置(续4) 为本 例2.2.11 已知 , 4 3 2 1 , 5 3 0 4 2 1 = A = B 求 T T B A . T T T T 5 3 0 4 2 1 4 3 2 1 B A = = 5 4 3 2 0 1 1 3 2 4 . 19 28 11 16 1 2 = 解 (方法一) . 河套大学《线性代数》课件 第二章 矩阵

水人 2.2.3矩阵的转置(续5) 尚本 解(方依二) AB= 2 3 16 4 28 故 2 1628 BA(49 对于矩阵A,如果满足A”=A,则称A是对称 矩阵而当A「=-A时,则称A是反对称矩阵 河套大学《线性代数》课件 第二章矩阵 快东骨司
快乐学习 以人 2.2.3 矩阵的转置(续5) 为本 , 19 11 1 28 16 2 4 3 2 1 5 3 0 4 2 1 = AB = 解 (方法二) 故 ( ) . 19 28 11 16 1 T 2 T T B A = AB = A A = A T 对于矩阵 ,如果满足 , 则称 A 是对称 矩阵.而当 A = −A T 时,则称 A 是反对称矩阵. 河套大学《线性代数》课件 第二章 矩阵

水人 2.2.3矩阵的转置(续6) 尚本 对称矩阵的元素满足 ay=0(,j=1,2,,n 即以主对角线为对称轴的元素对应相等;反对称 矩阵的元素满足,=-4,=1,2,…,),从而 a,=0-1,2,,n),即主对角线上的元素都为 零,其它元素以主对角线为对称轴,对应元素 互为相反数 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 2.2.3 矩阵的转置(续6) 为本 河套大学《线性代数》课件 第二章 矩阵 对称矩阵的元素满足 a a (i , j 1, 2 , , n ) i j = j i = , 即以主对角线为对称轴的元素对应相等;反对称 矩阵的元素满足 a a (i , j 1, 2 , , n ) i j = − j i = ,从而 a 0(i 1, 2 , , n ), ii = = , 即主对角线上的元素都为 零,其它元素以主对角线为对称轴,对应元素 互为相反数