
第三章 线性方程组 目录 3.1线性方程组和高斯 (Gauss)消元法 3.2维向量组及向量组的线性组合 3.3向量组的线性相关性 3.4向量组的秩 3.5向量空间 四 3.6齐次线性方程组解的结构 3.7非齐次线性方程组解的结构 3.8应用举例 河套大学《线性代数》课件 第三章线性方程组 快乐学司
第三章 线性方程组 □ 3.1 线性方程组和高斯(Gauss)消元法 □ 3.2 维向量组及向量组的线性组合 □ 3.3 向量组的线性相关性 □ 3.4 向量组的秩 □ 3.5 向量空间 3.6 齐次线性方程组解的结构 □ 3.7 非齐次线性方程组解的结构 □ 3.8 应用举例 目录 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 n

本节授裸计划 水人 (2课时) 尚本 必复习 新课3.6 齐次线性方程组解的结构 第二十五次课 3.61齐次线性方程组有非零解的条件 3.62齐次线性方程组解的结构 必小结 思考题及答案提示 必练习、作业及参考答案 河套大学《线性代数》课件 第三章线性方程组 快乐学司
快乐学习 以人 为本 ❖复习 ❖新课 3.6 齐次线性方程组解的结构 3.6.1 齐次线性方程组有非零解的条件 3.6.2 齐次线性方程组解的结构 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 二 十 五 次 课 本节授课计划(2课时) 河套大学《线性代数》课件 第三章 线性方程组

水人 3.6齐次线性方程组解的结构 尚本 主题调 1.解空间 2.齐次线性方程 组的基础解系 3.全部解 通解) 返回 河套大学《线性代数》课件 第三章线性方程组 快东学司
快乐学习 以人 为本 主 题 词 3.6 齐次线性方程组解的结构 河套大学《线性代数》课件 第三章 线性方程组 1.解空间 2.齐次线性方程 组的基础解系 3.全部解(通解) 返回
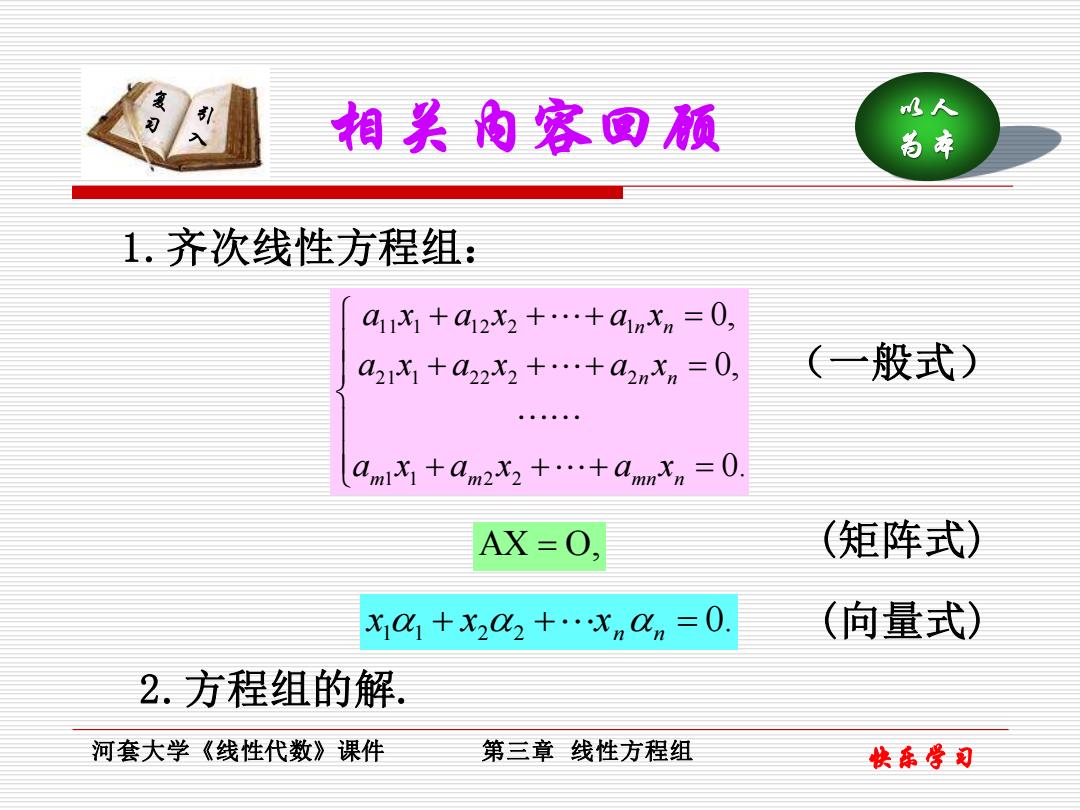
相关内容国预 人人 尚本 1.齐次线性方程组: 4111+a12X2+…+a1mXn=0, a21x1+a22X2+…+a2nXn=0, (一般式) amam2+amnn=0. AX=0, (矩阵式) xC必1+x202+xnCn=0, (向量式) 2.方程组的解 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
快乐学习 以人 相关内容回顾 为本 河套大学《线性代数》课件 第三章 线性方程组 1.齐次线性方程组: 2.方程组的解. + + + = + + + = + + + = 0. 0, 0, 1 1 2 2 21 1 22 2 2 11 1 12 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x (一般式) AX = O, (矩阵式) 0. x1 1 + x2 2 +xn n = (向量式)

水人 新课 3.6.1齐次线性方程组有非零解的条件1 尚幸 考虑n元齐次线性方程组 4X=0, (3.61) 其中A为mxn矩阵,显然X=O是AX=O的一个 解(称之为零解或平凡解 ),故齐次线性方(3.61) 总是相容的.那么齐次线性方程组(361)在什么 条件下有非零解(或只有零解)呢? 将齐次线性方程组(36.1)表示成向量形式: 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
以人 新课 3.6.1齐次线性方程组有非零解的条件 1 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 考虑 n 元齐次线性方程组 AX = O , (3.6.1) 其中 A 为 mn 矩阵. 显然 X = O 是 AX = O 的一个 解(称之为零解或平凡解),故齐次线性方(3.6.1) 总是相容的.那么齐次线性方程组(3.6.1)在什么 条件下有非零解(或只有零解)呢? 将齐次线性方程组(3.6.1)表示成向量形式:

水人 新课 3.6.1齐次线性方程组有非零解的条件2 尚本 x01+X2C2+xnQ,=0 显然,下列四个命题等价: (1)方程(3.6.1)有非零解; (2)存在不全为零的数x,x2,…,xn 使(3.6.2)成立 (3)向量组a,c,,a,线性相关; (4)R(A=R(@1,02,,Qn)<n 河套大学《线性代数》课件 第三章线性方程组 快东学日
以人 新课 3.6.1齐次线性方程组有非零解的条件 2 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 0. x1 1 + x2 2 +xn n = 显然,下列四个命题等价: (1) 方程(3.6.1)有非零解; (2) 存在不全为零的数 , , , 1 2 n x x x 使(3.6.2)成立; (3)向量组 n , , , 1 2 线性相关; (4) R(A) = R(1 ,2 , ,n ) n

水人 新课 3.6.1齐次线性方程组有非零解的条件3 尚本 于是又从一个角意得出下面的结论(即定理 3.1.2) 444444444404t444444440g 定理3.6.1设A是m×n矩阵,则齐次线性方程 组AX=O有非零解的充分必要条件是R(0<n■ 华水华米华米中本华中中华水华华华中中水年年华单华有华中*中华华华单华年中年水中中年年有有华*中4中中中华华年中中中年单年年中华◆年4中年中◆年年◆中4中华中年中中年中中中年中年年华年年中年中年年中单◆4年华◆中◆单◆华中年4年中华华年中◆◆年◆ 此定理的等价命题是: 设A是mxn矩阵, 则齐次线性方程组X=O只有零解的充要条件是 R(A)=n. 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
以人 新课 3.6.1齐次线性方程组有非零解的条件 3 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 于是又从另一个角度得出下面的结论(即定理 3.1.2): 定理3.6.1 设 A 是 mn 矩阵,则齐次线性方程 组 AX = O 有非零解的充分必要条件是 R(A) n . 此定理的等价命题是:设 A 是 mn 则齐次线性方程组 AX = O 只有零解的充要条件是 R(A) = n. 矩阵

水人 新课 3.6.1齐次线性方程组有非零解的条件4 尚本 推论36.1设A是m×n矩阵,则 中中中中中 1.当m<n时,齐次线性方程组AX=O必有 非零解; 2.当 m=n时,齐次线性方程组AX=O有 非零解(只有零解)的充要条件是 A=0(4≠0) 河套大学《线性代数》课件 第三章线性方程组 快乐学司
以人 新课 3.6.1齐次线性方程组有非零解的条件 4 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 推论3.6.1 设 A 是 mn 矩阵,则 1.当 m n 时,齐次线性方程组 AX = O 非零解; 2.当 m = n 时,齐次线性方程组 AX = O 必有 非零解(只有零解)的充要条件是 A = 0 有 ( A 0)

水人 新课 3.6.1齐次线性方程组有非零解的条件5 本 例3.6.1 试判断当入为何值时,齐次线性 方程组 x1+2x2+x3=0, X1-X2+X3=0, 2x+x2+2x3=0 (1)有非零解;(2)只有零解 解(解一)将齐次线性方程组的系数矩阵 A进行初等行变换 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
以人 新课 3.6.1齐次线性方程组有非零解的条件 5 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 例3.6.1 试判断当 为何值时,齐次线性 方程组 + + = − + = + + = 2 0. 0, 0, 1 2 3 1 2 3 1 2 3 x x x x x x x x x (1)有非零解;(2)只有零解. 解 (解法一 )将齐次线性方程组的系数矩阵 A 进行初等行变换

0人 新课 3.6.1齐次线性方程组有非零解的条件6 尚本 0元+1 0 +(=1)x A= r3+(-)× 01+12-入 1 -1 r<今12 0 λ+1 0 3+(-1)×2 002-九 当1=2或1=1时,R(A)=2<3; 当1≠2或2≠1时,R(4)=3 河套大学《线性代数》课件 第三章线性方程组 快东学司
以人 新课 3.6.1齐次线性方程组有非零解的条件 6 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 = − 1 2 1 1 1 1 1 A 3 2 1 2 r r r r + − + − ( λ) ( 1) + − − + 0 1 2 1 1 1 0 1 0 3 2 1 2 r r r r + − ( 1) . 0 0 2 0 1 0 1 1 1 − + − 当 = 2或 = −1时,R(A) = 2 3 ; 当 2或 −1时,R(A) = 3