
鍇论 高等数学少学时 绪论 一、现实生活中的数学问题 二、高等数学的基本思想方法 三、为什么要学?学什么?怎样学? 北京邮电大学出版社
2 绪 论 一、现实生活中的数学问题 二、高等数学的基本思想方法 三、为什么要学?学什么?怎样学?

论 高等敦学少学时 一、现实生活中的数学问题 经典数学一研究现实世界中的数量关系和空间形式. 在自然界中,到处都渗透着数学的思想和法则.例如: ① 如果扔一块肉骨头给狗狗一定沿直线奔过去 两点之间线段最短 2 蜂巢的截面是正六边形的 表面积最小容积最大 两端固定的一条柔软绳子,它必然呈悬连线的形状 中心位置最低(总位能最小) 奇妙的自然界按照数学的法则创造了世界,数学的规律 是宇宙的精髓,数学是开启宇宙奥秘之门的钥匙, 北京邮电大学出版社 3
3 一、现实生活中的数学问题 经典数学—研究现实世界中的数量关系和空间形式. 在自然界中,到处都渗透着数学的思想和法则.例如: ① 如果扔一块肉骨头给狗,狗一定沿直线奔过去 ——两点之间线段最短 ② 蜂巢的截面是正六边形的 ——表面积最小容积最大 ③ 两端固定的一条柔软绳子,它必然呈悬连线的形状 ——中心位置最低(总位能最小) 奇妙的自然界按照数学的法则创造了世界,数学的规律 是宇宙的精髓,数学是开启宇宙奥秘之门的钥匙

鍇论 高等数学少学时 二、高等数学的基本思想方法 初等数学的主要研究对象—常量 高等数学的主要研究对象— 变量 ①变速直线运动的速度问题 —以不变代变 S V= t T to h t2 titi in tn t 北京邮电大学出版社
4 二、高等数学的基本思想方法 初等数学的主要研究对象——常量 高等数学的主要研究对象——变量 ①变速直线运动的速度问题 ——以不变代变 t s v = t T1 T2 0 t 1 t 2 t i−1 t i t n−1 t n t i
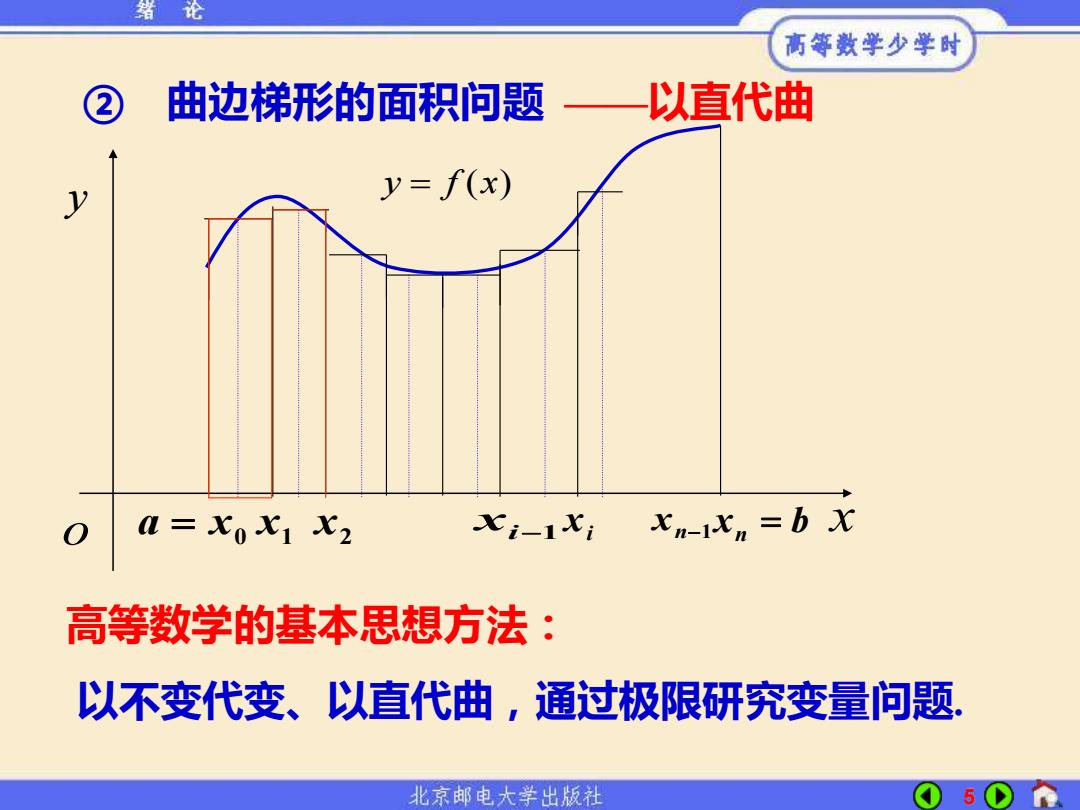
鍇论 高等数学少学时 ② 曲边梯形的面积问题 一以直代曲 y y=f(x) 0=x0X1X2 x-1X: xn-1xn=b x 高等数学的基本思想方法: 以不变代变、以直代曲,通过极限研究变量问题. 北京邮电大学出版社 5
5 x y y = f (x) o a = x0 x1 xi−1 xi xn−1 xn = b x2 ② 曲边梯形的面积问题 ——以直代曲 高等数学的基本思想方法: 以不变代变、以直代曲,通过极限研究变量问题

鍇论 高等数学少学时 三、为什么要学?学什么?怎样学? 1.为什么要学高等数学 一门科学,只有当它成功地运用数学时, 才能达到真正完善的地步: 马克思 要辨证而又唯物地了解自然,就必须熟 悉数学 恩格斯 高等数学是理、工、医、农类等院校学生学习的基石 北京邮电大学出版社 6
6 三、为什么要学?学什么?怎样学? 1.为什么要学高等数学 马克思 恩格斯 要辨证而又唯物地了解自然 ,就必须熟 悉数学. 一门科学, 只有当它成功地运用数学时, 才能达到真正完善的地步. 高等数学是理、工、医、农类等院校学生学习的基石

鍇论 高等数学少学时 2.学习内容 一元函数微分学(1一3) 内容 一元函数积分学(4一5) 微分方程(6) 数学的思想方法 北京邮电大学出版社 7
7 2.学习内容 数学的思想方法 一元函数微分学(1—3) 内容 一元函数积分学(4—5) 微分方程(6)

鍇论 高等数学少学时 3.怎样学 熊明在于学司,天才在于积累. 学而优则用,学而优则创· 由薄到厚,由厚到薄。 华罗庚 学习数学最好的方式是做数学, 北京邮电大学出版社 8
8 3. 怎样学 聪明在于学习, 天才在于积累. 学而优则用 , 学而优则创 . 由薄到厚 , 由厚到薄 . 华罗庚 学习数学最好的方式是做数学