
第华章 导数与微分 高等数学少学时 第四节微分及其适算 一、 微分的定义 二、微分的几何意义 三、微分的公式及运算法则 四、微分应用举例 北京邮电大学出版社 O1
1 第四节 微分及其运算 一、 微分的定义 二、 微分的几何意义 三、 微分的公式及运算法则 四、 微分应用举例

第三章导数与微分 高等数学少学时 微分的定义 1.引例一一函数增量的构成 Xo x 正方形的金属薄片受温度的影响, x x 其边长由x变到xo+△x面积增加了多少? 正方形边长与面积的函数关系式为 A=x好 xo 4cxo A=x2 当边长的增量为x时,面积的增量为 △M=(x+△x)2-x=2x△x+△2x 当△x→0时,是比 △x高阶的无穷小 △x的线性式是函数增量的主要部分 北京邮电大学出版社 2
2 一、 微分的定义 1.引例—— 函数增量的构成 2 A = x A x x x x x x 2 0 2 0 2 = ( 0 + ) − = 2 + 2 A = x0 x0x x0x x 2 x0 x x0 x 正方形边长与面积的函数关系式为 正方形的金属薄片受温度的影响, 其边长由x0变到x0+ Δx面积增加了多少? 当边长的增量为Δx时,面积的增量为 x的线性式,是函数增量的主要部分 高阶的无穷小 当 时 是比 x x → 0

第东章 导数与微分 高等数学少学时 定义设函数y=fx)在某一区间内有定义,K及x+x在 该区间内,如果y=f(x。+x)-f(x)可表示为 △y=A△x+o(△x) 其中A与△x无关,那么称函数y=fx)在点x是可微分的,而A△x 叫做函数y=f(x)在点x的微分,记作dy,即 =A△x 注△y=A△x+O(△x)中,也称dy是△y的线性主部. 显然,当△x很小时,有△y≈少. 北京邮电大学出版社 3
3 y = Ax +(x) dy = Ax 设函数 y =f (x)在某一区间内有定义,x0及x0+ Δx在 该区间内,如果 y = f (x0 + x) − f (x0 )可表示为 注 y = Ax +(x) 中,也称 dy 是y 的线性主部. 显然,当x很小时,有 y dy. 定义 其中A与Δx无关,那么称函数y=f (x)在点x0是可微分的,而AΔx 叫做函数 y =f (x)在点x0的微分,记作dy,即

第二章导数与微分 高等数学少学时 2.导数与微分的关系 设函数y=f(x)在点x,可微,则△y=A△x+o(△x), Ay =A+ (△)∴.A= lim Ay =f'(xo). △x→0 △x △x 即f(x)在点x可导,且A=f'(x) 反之,如果f(w)在点x,可导,即1imA=f'x,)存在 Ax→0△ 由极限与无穷小的关系, Ay=f'(x)+a,其中ix=0. △x ∴.Ay=f'(x)△x+Ax=f'(x)△x+o(△x) 即函数y=f(x)在点x,可微. 北京邮电大学出版社
4 , ( ) x x A x y = + lim ( ). 0 0 f x x y A x = = → ( ) , 即f x 在点x0 可导 ( ). x0 且A = f 设函数y = f (x)在点x0 可微,则 lim ( ) . 0 0 即 f x 存在 x y x = → , ( ) , 反之 如果f x 在点x0可导 2. 导数与微分的关系 y = Ax +(x), ( ) , = 0 + f x x y y = f (x0 )x +x ( ) . 即函数y = f x 在点x0 可微 lim 0. 0 = → x 由极限与无穷小的关系, 其中 ( ) ( ). = f x0 x + o x

第三章导数与微分 高等数学少学时 定理y=f(x)在点x可导←=f(x)在点x可微. 注由dk=1·△x=△K,所以通常把△x称为自变量的微分, 记作k.于是y=f(x)的微分又可记作 少=f'(x)k 有 =f'(x) dx 即函数的微分与自变量的微分之商等于该函数的导数.因此,导数 也叫“微商”. 北京邮电大学出版社 5
5 定理 y = f (x)在点x0 可导 ( ) . y = f x 在点x0可微 注 记作dx. 于是y = f (x)的微分又可记作 dy = f (x0 )dx 由dx = 1x = x, 所以通常把Δx称为自变量的微分, 即函数的微分与自变量的微分之商等于该函数的导数.因此, 导数 也叫“微商”. ( ) x0 f dx dy 有 =

第华章 导数与微分 高等数学少学时 例1设y=x2,当r=2,△x=0.01时,求△y,y及△y-d. 解y=(x2)'d=2xdc, Ay=(x+△x}-x2=2xAx+(△x}. ∴.当r=2,△x=d=0.01时, Ay,=2xAc+acl3=2-20.01+0.01y=0.0401, c=0.01 ..dy2=2xA 2=2.2.0.01=0.04, △x=0.01 △x=0.01 (4y-4w)g21=0.0401-0.04=0.001 北京邮电大学出版社 6
6 例 1 2, 0.01 , . 2 设 y = x , 当x = x = 时,求y dy及y − dy ( ) 2 , 2 dy = x dx = xdx 当x = 2,x = dx = 0.01时, 2 0.01 2 0.01 2 == = = = xx x dy x x x 解 ( ) 2 ( ) . 2 2 2 y = x + x − x = xx + x ( ) 0.0 1 2 2 0.0 1 2 2 == = = = + xx x y x x x x 2 2 0.01 (0.01 ) 0.0401, 2 = + = = 2 2 0 .01 = 0 .04 , ( ) 0 .01 2 = − =x y dy x = 0.0401 − 0.04 = 0.0001
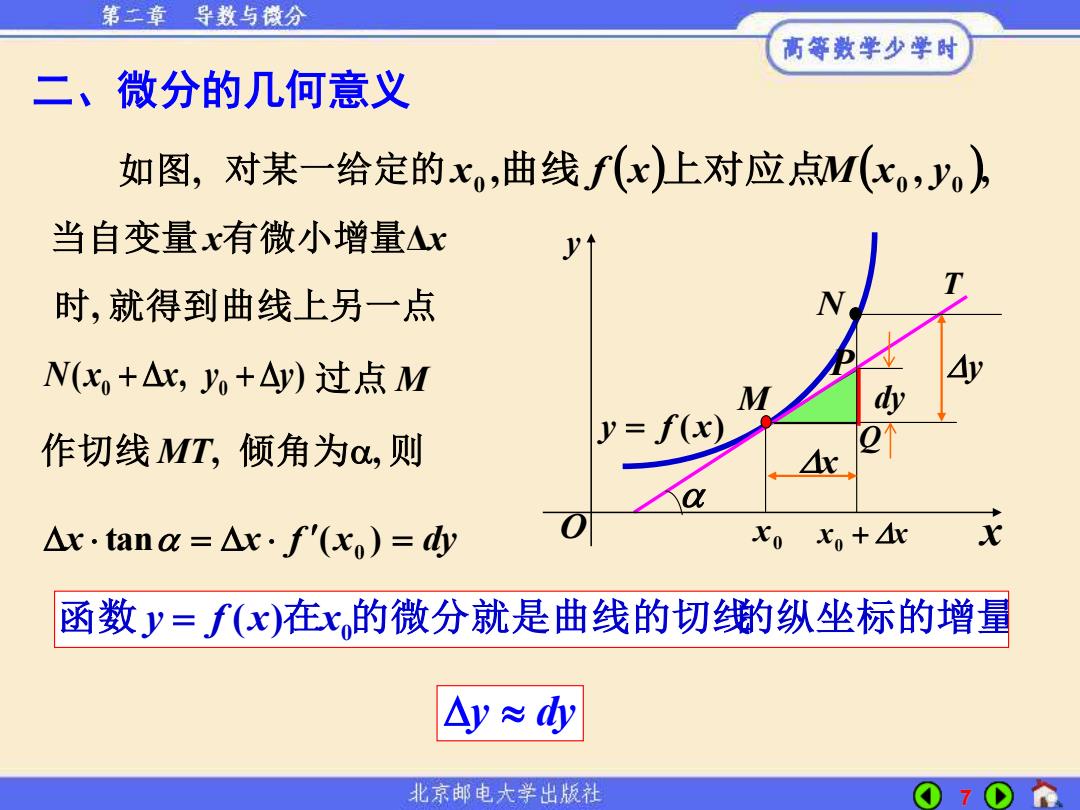
第三章导数与微分 高等数学少学时 二、微分的几何意义 如图,对某一给定的x,曲线f(x)上对应点M(xoy) 当自变量x有微小增量△x 时,就得到曲线上另一点 N(x,+△x,y+△y)过点M M 作切线MT,倾角为o,则 y=f(x) △x·tana=x·f'(xo)=y x0x。+ x 函数y=f(x)在x的微分就是曲线的切线的纵坐标的增量 △y≈ 北京邮电大学出版社
7 二、微分的几何意义 ( , ) 0 0 N x + x y + y 作切线 MT, 倾角为, 则 时, 就得到曲线上另一点 当自变量 x有微小增量Δx 如图, , ( ) ( , ), 0 0 0 对某一给定的 x 曲线 f x 上对应点M x y tan ( ) x0 x = x f = dy 函 数 y = f (x)在x0 的微分就是曲线的切线的纵坐标的增量 y dy 过点 M y = f (x) M N Q T P x y dy x + x 0 0 x x y O

第工章导数与微分 高等数学少学时 三、微分的公式及运算法则 1.基本初等函数的微分公式 (1) (c)=0, d(c=0, (2) ()=a, d(x")=pxa-Idx, (3) (sinx)=cosx, d (sinx)=cosxdx, (④)(cosx)=-sinx, d(cosx)=-sinxdx, (tanx)=secx, d (tanx)=sec xdx, (6) (cotx)=-csc'x, d(cotx)=-csc2xdx, (7)(secx)=secxtanx,d(secx)=secxtanxox, ⑧)(csex)=-cscxcot.x, d(cscx)=-cscxcotxdx, 北京邮电大学出版社
8 1. 基本初等函数的微分公式 (1) (C) = 0, d (C) = 0, (2) ( ) , −1 = x x ( ) , 1 d x x dx − = (3) (sin x) = cos x, d (sin x) = cos xdx, (4) (cos x) = −sin x, d(cos x) = −sin xdx, 三、微分的公式及运算法则 (5) (tan ) sec , 2 x = x (tan ) sec , 2 d x = xdx (6) (cot ) csc , 2 x = − x (cot ) csc , 2 d x = − xdx (7) (secx) = secx tan x, d (secx) = secxtan xdx, (8) (csc x) = −csc x cot x, d (csc x) = −csc xcot xdx

第章 导数与微分 高等数学少学时 9(a)=ana, d(a*)=a*Inadx, o)(e)=e, de)=e"dx, )ogr)=1 d(o. 2)血=女 d(Inx)=-dx, 创sa。 en小 间(ac京 uos小-血, )(a=1十 at时-十k 北京邮电大学出版社 9
9 (9) (a ) a lna, x x = d (a ) a lnadx, x x = (10) ( ) , x x e = e d(e ) e dx, x x = ( ) ( ) , ln 1 11 loga x a x = ( ) , ln 1 log dx x a d a x = ( ) ( ) , 1 12 ln x x = ( ) , 1 ln dx x d x = ( ) ( ) , 1 1 13 arcsin 2 x x − = ( ) , 1 1 arcsin 2 dx x d x − = ( ) ( ) , 1 1 14 arccos 2 x x − = − ( ) , 1 1 arccos 2 dx x d x − = − ( ) ( ) , 1 1 15 arctan 2 x x + = ( ) , 1 1 arctan 2 dx x d x + =

第章 导数与微分 高等数学少学时 =4女ri时=2a 2.微分的四则运算法则 设u=(x,v=(x)可微分,则有 ((u±)=W±, d(u±)=du±d, (2)(uv)='y+uv, d(uv)=vdu+udy, (3)(C=Cu(c是常数) d(Cu)=Cdu, 4) 〔)“w咖。叭 北京邮电大学出版社 010
10 ( ) ( ) , 1 1 16 arc cot 2 x x + = − ( ) . 1 1 arc cot 2 dx x d x + = − 设u = u(x),v = v(x)可微分,则有 2. 微分的四则运算法则 (1) (u v) = u v , d(u v)= du dv, (Cu) = Cu (C是常数), (3) d(Cu) = Cdu, (2) (uv) = u v + uv , d(uv) = vdu+ udv, (4) ( 0), 2 − = v v u v uv v u ( 0). 2 − = v v vdu udv v u d