
第三章 微分中值定理与导数的应用 高等数学少学时 第五节品数的极值 与最大值最小值 一、函数的极值及其求法 二、函数的最大最小值问题 北京邮电大学出版社
1 第五节 函数的极值 与最大值最小值 一、函数的极值及其求法 二、函数的最大最小值问题

第三章微分中值定理与导数的应用 高等数学少学时 一、函数的极值及其求法 定义设函数f(x)在区间(,b)内有定义,x。∈(a,b). 如果存在着点x,的一个去心邻域,从这去心邻域内任取一点 x,都有f(x)f(x),那么称f(x)是函数 f(x)的一个极大小值. 函数的极大值与极小值统称为函数的极值,使函数取得 极值的点称为极值点. 函数的极大值和极小值的概念是局部性的.如下图 北京邮电大学出版社 2
2 一、函数的极值及其求法 定义 设函数 f x( ) 在区间 ( , ) a b 内有定义, 0 x a b ( , ). 如果存在着点 0 x 的一个去心邻域, 从这去心邻域内任取一点 x, 函数的极大值与极小值统称为函数的极值,使函数取得 极值的点称为极值点. 函数的极大值和极小值的概念是局部性的.如下图 都有 0 f x f x ( ) ( ) 0 ( ( ) ( )), f x f x 那么称 0 f x( ) 是函数 f x( ) 的一个极大(小)值
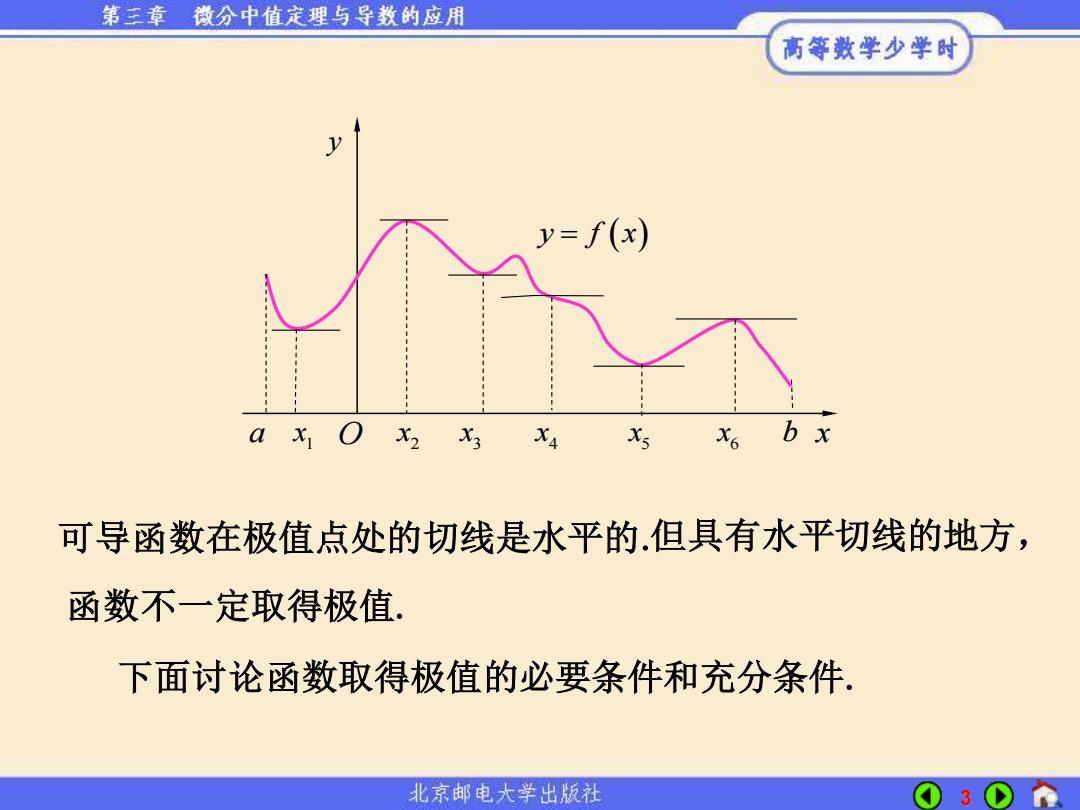
第三章 微分中值定理与导数的应用 高等数学少学时 y=f(x) x6 b x 可导函数在极值点处的切线是水平的.但具有水平切线的地方, 函数不一定取得极值. 下面讨论函数取得极值的必要条件和充分条件. 北京邮电大学出版社 3
3 可导函数在极值点处的切线是水平的. 函数不一定取得极值. 但具有水平切线的地方, 下面讨论函数取得极值的必要条件和充分条件. a x1 O x2 x3 x4 x5 x6 b y f x = ( ) y x

第三章 微分中值定理与导数的应用 高等数学少学时 定理1(必要条件)设函数f(x)在点x,处可导,且在x 处取得极值,那么f'(x)=0. 证设f(x)是极大值.由于函数f(x)在点x。处可导, 根据导数定义"(x,)=im f(x)-f() x-x0 x-xo x时, (x-fx】<0 因此lim f(s)-f(x≤0. x-xo x→x0 x-xo 故f'()=0. 使得导数等于零的点(即方程'(x)=0的实根),叫做函数 f(x)的驻点. 北京邮电大学出版社
4 定理1(必要条件) 设函数 f (x) 在点 0 x 处可导,且在 0 x 处取得极值,那么 f x ( 0 ) = 0. 证 设 f x( 0 ) 是极大值. 由于函数 f (x) 在点 0 x 处可导, 根据导数定义 ( ) ( ) ( ) 0 0 0 0 lim . x x f x f x f x → x x − = − 0 x x 时, ( ) ( 0 ) 0 0 f x f x x x − − 因此 ( ) ( ) 0 0 0 lim 0; x x f x f x x x → − − − 0 x x 时, ( ) ( 0 ) 0 0 f x f x x x − − 因此 ( ) ( ) 0 0 0 lim 0. x x f x f x x x → − − − 故 f x ( 0 ) = 0. 使得导数等于零的点(即方程 f x ( ) = 0 的实根),叫做函数 f x( ) 的驻点
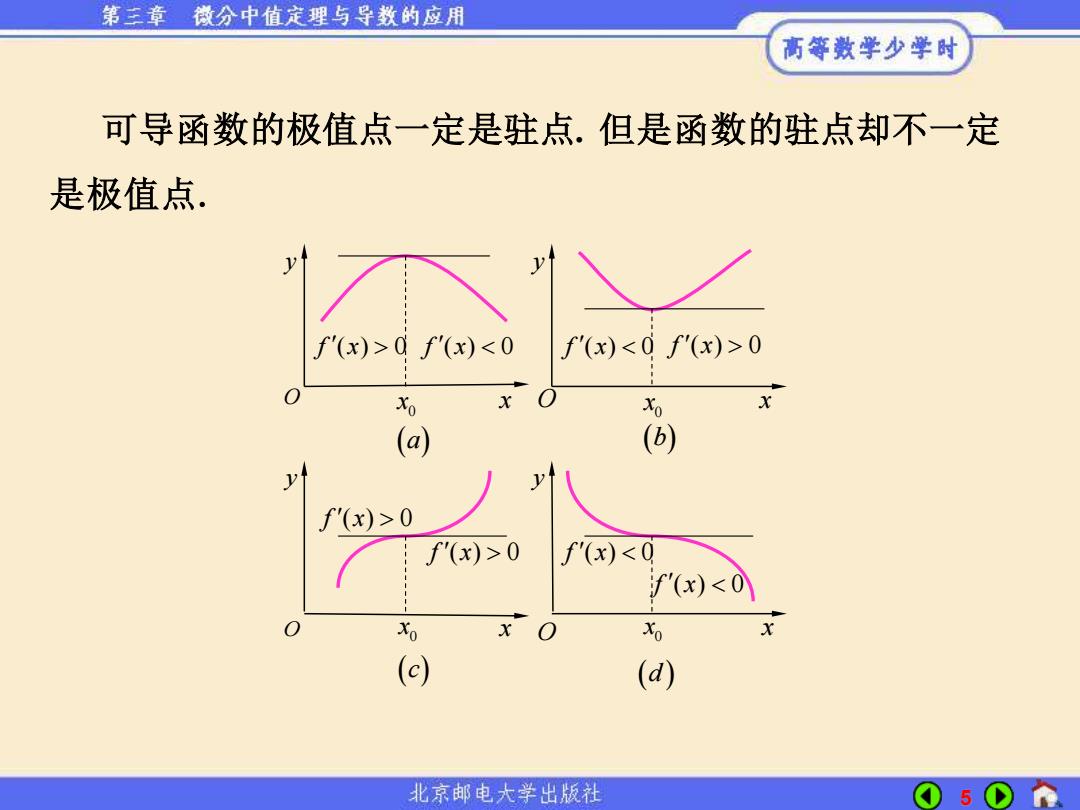
第三章 微分中值定理与导数的应用 高等数学少学时 可导函数的极值点一定是驻点.但是函数的驻点却不一定 是极值点. y f'(x)>0f'(x)0 Xo X 0 (a) (b) f)>0 f'(x)>0 f'(x)<0 f'(x)<0 Xo O 0 (c) (d) 北京邮电大学出版社 5
5 可导函数的极值点一定是驻点. 但是函数的驻点却不一定 是极值点. O O O O x x x y y y y 0 x 0 x 0 x 0 x x (a) (b) (c) (d ) f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0 f x ( ) 0

第三章 微分中值定理与导数的应用 高等数学少学时 定理2(第一充分条件)设函数f(x)在xo处连续,且在 x0的某6去心邻域内可导. (1)若x∈(x。-6,xn)时,f'(x)>0,而x∈(x,x+6)时, f'(x)0,则f(x)在x。处取得极小值; 3)若在x,的某6去心邻域内f'(x)符号保持不变,则 f(x)在xo处没有极值. 北京邮电大学出版社 6
6 定理2(第一充分条件) 设函数 f (x) 在 x0 处连续, 且在 x0 的某 去心邻域内可导. ⑴ 若 ( ) 0 0 x x − , x 时, f x ( ) 0; 而 ( + ) 0 0 x x , x 时, f x ( ) 0, 则 f (x) 在 0 x 处取得极大值; ⑵ 若 ( ) 0 0 x x − , x 时, f x ( ) 0; 而 ( + ) 0 0 x x , x 时, f x ( ) 0, 则 f (x) 在 0 x 处取得极小值; ⑶ 若在 x0 的某 去心邻域内 f (x) 符号保持不变, 则 f (x) 在 0 x 处没有极值

第三章 微分中值定理与导数的应用 高等数学少学时 求函数的极值的一般步骤: (I)求出f'(x): (2)令f'(x)=0,求出fx)的所有驻点, 和使∫x)的导数不存在的点(若有的话); (3)分别考察f'(x)在以上各个点的左右邻近两侧的符号, 以确定该点是否为极值点,是极大值点还是极小值点; (4)求出函数的所有极值. 北京邮电大学出版社 7
7 求函数的极值的一般步骤: ⑶ 分别考察 f (x) 在以上各个点的左右邻近两侧的符号, 以确定该点是否为极值点,是极大值点还是极小值点; ⑷ 求出函数的所有极值. ⑵ 令 f (x) = 0, 求出f(x)的所有驻点, ⑴ 求出 f (x); 和使 f (x) 的导数不存在的点(若有的话);

第三章 微分中值定理与导数的应用 高等数学少学时 例1求函数f(x)=(x-5)x2的极值. 解01F+7-2 3 (2)令'(x)=0,得到驻点x=2; x=0时f'(x)不存在. (3)确定f'(x)的符号: 02时f'(x)>0.故x=2 是极小值点.又当x0.所以x=0 是极大值点. (4)极大值f(0)=0,极小值f(2)=-34. 北京邮电大学出版社 8
8 例1 求函数 ( ) ( ) 3 2 f x x x = − 5 的极值. 解 ⑴ ( ) ( ) ( ) 3 2 3 3 2 1 5 2 5 ; 3 3 x f x x x x x − = + − = ⑵ 令 f x ( ) = 0, 得到驻点 x = 2; x = 0 时 f x ( ) 不存在. ⑶ 确定 f x ( ) 的符号: 0 x 2 时 f x ( ) 0; x 2 时 f x ( ) 0. 故 x = 2 是极小值点. 又当 x 0 时 f x ( ) 0. 所以 x = 0 是极大值点. ⑷ 极大值 f (0 0, ) = 极小值 ( ) 3 f 2 3 4. = −

第三章 微分中值定理与导数的应用 高等数学少学时 定理3(第二充分条件)设函数f(x)在点x,处具有二阶 导数且f'(x)=0,f”"(x)≠0, (1)如果f"(x)>0,则函数f()在点X处取得极小值; (2)如果f"(x)<0,则函数f()在点飞,处取得极大值 定理3表明,如果函数f(x)在驻点Xo处的二阶导数 f"(x)≠0,那么该驻点x,一定是极值点.但如果f”(x)=0, 定理3失效,此时,可用其他方法判定, 北京邮电大学出版社
9 定理3(第二充分条件) 设函数 f x( ) 在点 0 x 处具有二阶 导数且 0 f x ( ) 0, = 0 f x ( ) 0, ⑴ 如果 0 f x ( ) 0, 则函数 f x( ) 在点 0 x 处取得极小值; ⑵ 如果 0 f x ( ) 0, 则函数 f x( ) 在点 0 x 处取得极大值. 定理 3 表明, 如果函数 f x( ) 在驻点 0 x 处的二阶导数 f x ( 0 ) 0, 那么该驻点 0 x 一定是极值点. 但如果 f x ( 0 ) = 0, 定理 3 失效, 此时, 可用其他方法判定

第三章 微分中值定理与导数的应用 高等数学少学时 例2求函数f(x)=(x2-2)的极值, 解(1)f"()=6x(x2-2. (2)令f"(x)=0,求得驻点x1=-V2,x,=0,x=√2 (3)f"(x)=6(r2-2(52-2: (4)因f"(0)=24>0,故f()在x=0处取得极小值, 极小值为f(0)=-8. ⑤)f"(-2)=f"(2)=0,用定理3无法判别.考察一阶导数 在驻点x=-√2及飞=√2左右邻近的符号: 当-√2<x<0时,f'(x)<0:当x<-√2时,f'(x)<0 因为f'(x)的符号没有改变,所以f(x)在x1=-√2处没有极值 北京邮电大学出版社 10
10 例2 求函数 ( ) ( ) 3 2 f x x = − 2 的极值. 解 (1) ( ) ( ) 2 2 f x x x = − 6 2 . (2) 令 f x ( ) = 0, 求得驻点 1 x = − 2, 2 x = 0, 3 x = 2. (3) ( ) ( )( ) 2 2 f x x x = − − 6 2 5 2 . (4) 因 f (0 24 0, ) = 故 f x( ) 在 x = 0 处取得极小值, 极小值为 f (0 8. ) = − (5) f f ( 2 2 0, ) ( ) − = = 用定理 3 无法判别. 考察一阶导数 在驻点 1 x = − 2 及 3 x = 2 左右邻近的符号: 当 − 2 0 x 时, f x ( ) 0; 当 x − 2 时, f x ( ) 0; 因为 f x ( )的符号没有改变,所以 f x( )在 1 x = − 2 处没有极值