
第一章 函数与极限 高等数学少学时 第一章司数保 一、函数 二、极限 三、函数的连续与间断 北京邮电大学出版社 01
1 第一章 习题课 一、函数 二、极限 三、函数的连续与间断

第一章函数与极限 高等数学少学时 一、函数 1.函数定义① 定义:f:D→fD)定义域 值域 ② 反函数 ③ 复合函数 2.性质 ① 有界性 ② 单调性 )奇偶性 ④ 周期性 3.初等函数 由常数及基本初等函数经有限次四则运算和有限次复合 得到的能用一个表达式的函数 北京邮电大学出版社 2
2 一、函数 1.函数定义 ① 定义: 定义域 值域 ② 反函数 ③ 复合函数 f : D → f (D) 2.性质 ① 有界性 ② 单调性 ③ 奇偶性 ④ 周期性 3.初等函数 由常数及基本初等函数经有限次四则运算和有限次复合 得到的能用一个表达式的函数

第一章 函数与极限 高等数学少学时 例1判断下列函数是否为初等函数?为什么? o/m/ 紫W安所以是初等西数 (2)f(x)=1-√x,x∈R,所以fx)是初等函数. 例2设(=x+1+(>0以求() 解令 是则x=如>以代入得 r=1+6a>以)=++(c>0吵 北京邮电大学出版社 3
3 例1 . 1 , 0 1 , 0, (2) ( ) 3 3 + − = x x x x ; f x 1, 0 1, 0, (1) ( ) − = x x f x (1) ( ) , 2 x x f x = (2) ( ) 1 , , 6 f x = − x x R 判断下列函数是否为初等函数 ? 为什么 ? 解 所以f (x)是初等函数. 所以f (x)是初等函数. 1 ( 0), ( ) . 1 2 x x x f x x f = + + 求 解 令 则 ( 0),代入得 1 , 1 = = u u u x x ( ) ,( 0), 1 1 1 2 = + + u u u f u ( ) ( 0). 1 1 1 2 = + + x x x f x 例2 设

第一章 函数与极限 高等数学少学时 例3分解下列函数: D y-m(tan )2)y=aresin 解1)y=n(tanx)由y=lnw,u=anx复合而成 2y-aresinv1+xy-t,u-aresimv.v-vw,w-1+x 四个函数复合而成. 北京邮电大学出版社
4 1 ln(tan ), 2) (arcsin 1 ) . 2 2 )y = x y = + x 例3 分解下列函数: 解 2) (arcsin 1 ) 2 2 y = + x 四个函数复合而成. 1) y = ln(tan x)由 y = ln u,u = tan x 复合而成. 2 2 由 y = u ,u = arcsin v,v = w,w = 1+ x

第一章 函数与极限 高等数学少学时 练习1 1.下列各组函数是否相同?为什么? w-5与-*-a-】 相同 e=公,与国= 相同 2.分解下列函数: 2x 1)y=sin +X,由y=sim 2x 1+x2 复合而成 2y=em.由y=e“,u=sim,y= 1 复合而成. X 北京邮电大学出版社 5
5 1.下列各组函数是否相同 ? 为什么? = a x a x x a f x , , , (1) ( ) ( ) . 2 1 ( ) 2 与 x = a + x − a − x = , 0 0, 0, (2) ( ) x x x f x 与(x) = f [ f (x)]. 相同 相同 练习1 , 1 2 1) sin 2 x x y + = 2) . 1 sin x y = e 2. 分解下列函数: . 1 2 sin , 由 2 复合而成 x x y u u + = = x y e u v v u 1 由 = , = sin , = 复合而成

第一章函数与极限 高等数学少学时 二、极限 数列极限“&一N” 1.概念 fx→x。"ε一8”左右极限 函数 x)o,"e一X"单侧极限 唯一性 2.性质 有界性 保号性 北京邮电大学出版社 6
6 二、极限 1.概念 数列极限 “ε—N” 函数 x → x0 " —" x → , " — X" 2. 性质 唯一性 有界性 保号性 左右极限 单侧极限
第一章 函数与极限 高等数学少学时 3.无穷小与无穷大 无穷小的性质 无穷小的比较 4.四则运算法则 夹逼准则 5.存在准则 单调有界数列必有极限 6.两个重要极限 ()1imsm巴-1( S1n▣ 或lim(l+o)=e 口→0 ②m1+是e 注口代表相同的表达式 7.求极限的基本方法 北京邮电大学出版社 7
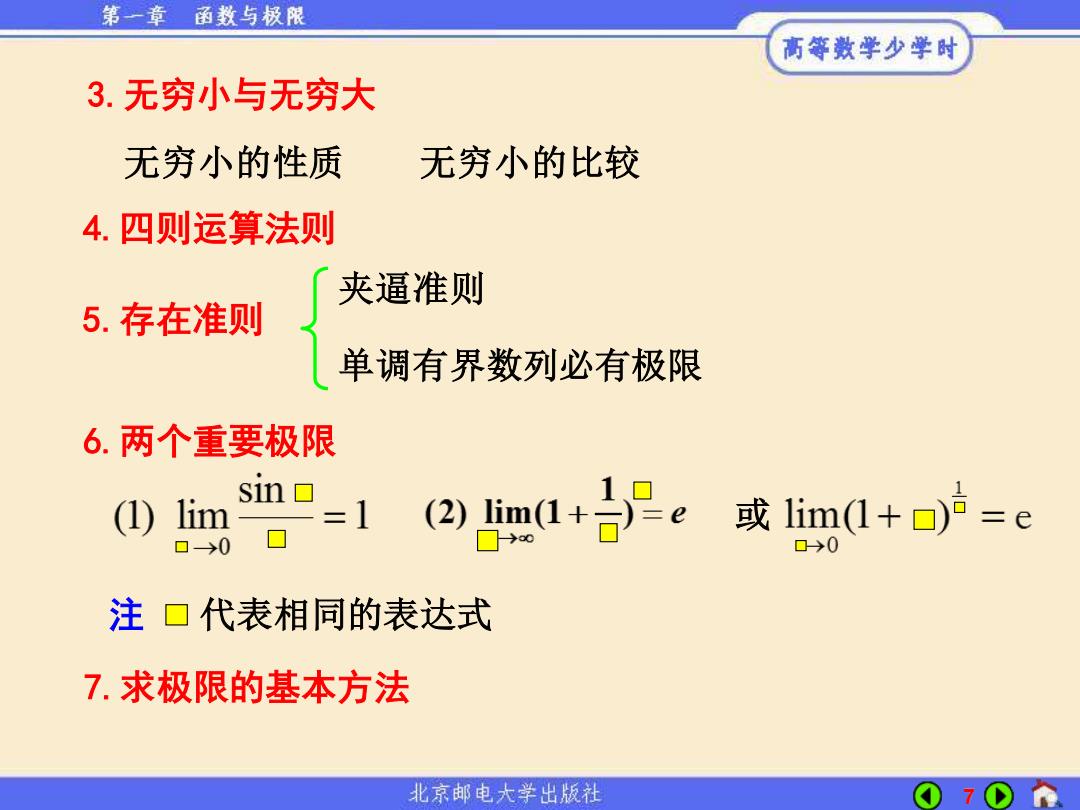
7 5.存在准则 夹逼准则 单调有界数列必有极限 4.四则运算法则 6.两个重要极限 或 注 代表相同的表达式 3.无穷小与无穷大 无穷小的性质 无穷小的比较 7.求极限的基本方法

第一章 函数与极限 高等数学少学时 例4求下列极限 ④imn+1-n )(2) lim (2x-3)20(3x+2)30 →00 (2x+1)50 -小a哥 n+i+in) 30 (2x-3)20(3x+2)30 2 3+ 2 30 (2) lim lim 3 X→00 (2x+1)50 X-→0 2 北京邮电大学出版社 8
8 例4 求下列极限 (1) lim( n 1 n), n + − → . (2 1) (2 3) (3 2) (2) lim 50 20 30 + − + → x x x x ( )( ) ( n n) n n n n n + + + − + + = → 1 1 1 lim ( ) 0 1 1 lim = + + = n→ n n 解 ( n n) n + − → (1) lim 1 50 20 30 1 2 2 3 3 2 lim + + − = → x x x x 50 20 30 (2 1) (2 3) (3 2) (2) lim + − + → x x x x 30 2 3 =

第一章 函数与极限 高等数学少学时 例5求下列极限(1)lim 1-x2 1-cosx (2)lim x-→1Sinπx x→0 x2 2 3)im1+3;( 四* 解 ()im 1-x2 t=x-1 lim 1-t+2) x-→1 sinn x 0sinn(t+1) lim t(t+2) 元t lim lim (t+2) 2 t→0 sinπt t→0 sinπt t→0 元 元 2 2sin2 x sin 1-cosx 1 lim 2 2 1 (2)lim x->0 x2 →0 x2 lim 2x-0 X 2 2 北京邮电大学出版社 9
9 解 2 2 0 2 2sin lim x x x→ = 例5 求下列极限 ; sinπ 1 (1) lim 2 1 x x x − → t = x −1 sinπ( 1) ( 2) lim 0 + − + → t t t t 2 π = 0 ( 2) lim t sinπ t t → t + = 0 0 ( 2) lim lim t t sinπ π t t → → t + = x x x sinπ 1 (1) lim 2 1 − → 2 0 2 2 sin lim 2 1 = → x x x (3) lim(1 3 ) ; 2 0 x x + x → . 2 1 2 3 (4)lim x x x x + + →

第一章 函数与极限 高等数学少学时 8rga4n-a-=e 2 x->0 w时2 +分 1 三 1 e 北京邮电大学出版社 100
10 t t t t t 1 1 1 lim 1 lim 1 + = + → → x x x x + + → 2 1 2 3 (4)lim 2 2 +1 = x t x x x + = + → 2 1 2 lim 1 = e x x x 2 0 (3) lim(1+ 3 ) → 6 3 1 0 lim (1 3 ) = + → x x x 6 = e 1 1 2 lim 1 t t t − → +