
第女章 导数与微分 高等数学少学时 第二章导数写般分 第一节 导数的概念 第二节 函数的求导法则 第三节 高阶导数 第四节 微分及其运算 第二章习题课 北京邮电大学出版社
1 第二章 导数与微分 第一节 导数的概念 第二节 函数的求导法则 第三节 高阶导数 第四节 微分及其运算 第二章习题课

第工章导数与微分 高等数学少学时 第一节导数的撬念 函数的变化率 二、导数的定义 三、导数的几何意义 四、函数的可导性与连续性的关系 北京邮电大学出版社 2
2 第一节 导数的概念 一、 函数的变化率 二、 导数的定义 三、 导数的几何意义 四、 函数的可导性与连续性的关系

第华章 导数与微分 高等数学少学时 函数的变化率 在许多实际问题中,不仅要研究变量之间的函数关系,还 需要讨论变量与变量之间的相对变化情况.看下面的几个例子 例1过点(x,和(x,,)的直线-,=(x-x)的斜率为 k=- 24 X1-X0 △x 斜率是线性函数 y=(x-x)+ 从x变到x时的平均变化率. 北京邮电大学出版社 3
3 一、 函数的变化率 过 点(x0 , y0 )和(x1 , y1 )的直线y − y0 = k(x − x0 )的斜率为 . 1 0 1 0 x y x x y y k = − − = ( ) 0 0 y = k x − x + y 需要讨论变量与变量之间的相对变化情况.看下面的几个例子. 从x0变到x1时的平均变化率. 在许多实际问题中,不仅要研究变量之间的函数关系,还 例1 斜率是线性函数

第车章 导数与微分 高等数学少学时 例2设作匀速直线运动的物体的位置函数为s=s(),当物体 从时刻运动到t+△t(0<<+△)时,位置函数由s=s()变到 S=s(t+△),在时间间隔△t内,物体的平均速度为 s6+△)-s,)_As △t △t 物体的平均速度y是位置函数s=s(t)从到t+△t的平均变化率. 例3已知一条长度为的均匀细杆,以它的一端作为零点, 分别量取长度l,l2(L1<12<,相应细杆的质量分别是m1,m2,则细杆 在,这一段上的平均线密度为 p= n2-m1△m 12-1 相应细杆的线密度p是常数.p是m)从l1到l,2的平均变化率. 北京邮电大学出版社
4 设作匀速直线运动的物体的位置函数为s=s (t),当物体 从时刻 t0运动到 t0+Δt (0<t0<t0+Δt)时,位置函数由s=s(t0 )变到 s=s(t0+ Δt),在时间间隔Δt内,物体的平均速度为 ( ) ( ) t s t t s t v + − = 0 0 . t s = 已知一条长度为l的均匀细杆,以它的一端作为零点, 分别量取长度l1 , l2 (l1< l2<l),相应细杆的质量分别是m1 ,m2 ,则细杆 相应细杆的线密度ρ是常数. ρ是m=m( l )从l1 到l2的平均变化率. 在[l1,l2 ]这一段上的平均线密度为 2 1 2 1 l l m m − − = . l m = 例2 例3 物体的平均速度v是位置函数s=s( t )从t0 到t0+Δt的平均变化率

第东章 导数与微分 高等数学少学时 一般地,设函数fx)在xo,x1处有定义,记 △x=x1-xo,△y=f(x1)-fxo)=f(x+△x)-f(xo), 我们称 f(x+△x)-f(x)_4 y △x 为函数fx)从x变到xo+△x的平均变化率 例1中函数是线性的,例2、例3中都有均匀的假设,但在实 际问题中,我们遇到的函数绝大部分都是非线性的、非均匀的 问题,这些问题常常涉及到函数在一点的变化率问题, 北京邮电大学出版社
5 , ( ) ( ) ( ) ( ), 1 0 1 0 0 x0 x = x − x y = f x − f x = f x + x − f x y x f x x f x = ( + ) − ( ) 0 0 一般地,设函数f (x)在x0 , x1处有定义,记 我们称 为函数f (x)从x0变到x0+ Δx的平均变化率. 例1中函数是线性的,例2、例3中都有均匀的假设,但在实 际问题中,我们遇到的函数绝大部分都是非线性的、非均匀的 问题,这些问题常常涉及到函数在一点的变化率问题

第华章 导数与微分 高等数学少学时 例4变速直线运动的瞬时速度. 设某一物体作变速直线运动,在0,内走过的路程为s),物 体从t运动到。+△r0<t,t。+△t<t)的平均速度为 D=S(,+△)-s)△s △t △t 时间间隔越短,平均速度y越接近物体在时刻的瞬时速度,当 △t0时,如果上式的极限存在,则该极限为函数在时刻的瞬 时速度,记为 y lim s(t+△t)-s(to) △t→0 △t 也称v是函数s()在点的变化率. 北京邮电大学出版社 6
6 t 0运动到t 0 + t(0 t 0 ,t 0 + t t)的平均速度为 . ( ) ( ) 0 0 t s t s t t s t v = + − = . ( ) ( ) lim 0 0 0 t s t t s t v t + − = → 变速直线运动的瞬时速度. 体从 Δt→0时,如果上式的极限存在,则该极限为函数在时刻 t0的瞬 时速度,记为 也称v是函数s (t)在t0点的变化率. 例4 设某一物体作变速直线运动,在[0, t]内走过的路程为s (t),物 时间间隔越短,平均速度 越接近物体在t v 0时刻的瞬时速度,当
第华章 导数与微分 高等数学少学时 例5曲线在一点处切线的斜率. 一般地,设曲线C为函数y=f(x) y 的图形,M为C上的一点,N为C上 的另一点,直线MN是曲线C的一条 割线.当点W沿曲线C趋于点M时,如 0x+衣 果割线MN趋于它的极限位置MT,则 称直线MT为曲线C在点M处的切线. 北京邮电大学出版社 07
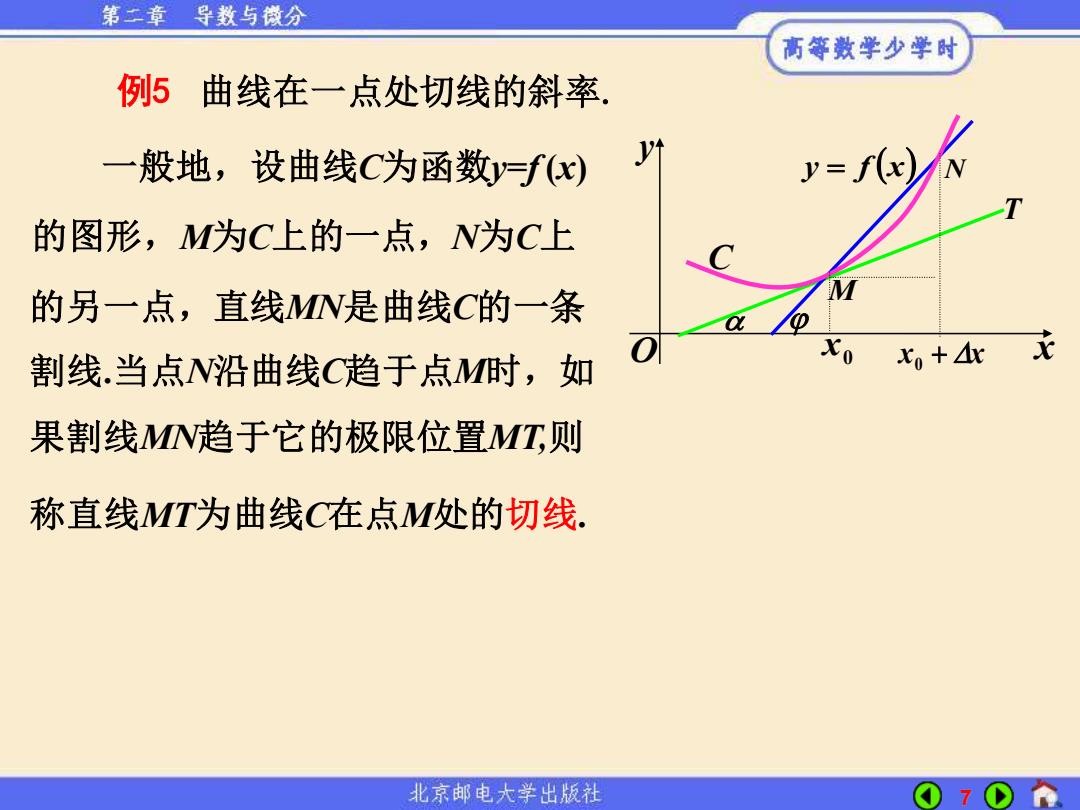
7 例5 曲线在一点处切线的斜率. 一般地,设曲线C为函数y=f (x) 的另一点,直线MN是曲线C的一条 O x y M N T x + x 0 x0 y = f (x) C 的图形,M为C上的一点,N为C上 割线.当点N沿曲线C趋于点M时,如 果割线MN趋于它的极限位置MT,则 称直线MT为曲线C在点M处的切线

第章 导数与微分 高等数学少学时 设M,N的坐标分别为(x,f(x)(x+△x,f(x+△),割线 MN的倾角为p,则割线的斜率为 f(x+△x)-f(x) △x 当点N沿曲线C趋于点M时(此时△x→0),如果上式的极限存 在,记为k,即 k=lim f(x,+△x)-f(xo) △x→0 △x 则极限值k就是切线MT的斜率这里=tana,a为切线MT的倾角.k 是函数y=f(x)在x处的变化率 北京邮电大学出版社
8 ( , ( )),( , ( )), 设M,N的坐标分别为 x0 f x0 x0 + x f x0 + x MN的倾角为φ,则割线的斜率为 割线 . ( ) ( ) tan 0 0 x f x x f x + − = 当点N沿曲线C趋于点M时(此时Δx→0),如果上式的极限存 在,记为k,即 , ( ) ( ) lim 0 0 0 x f x x f x k x + − = → 则极限值k就是切线MT的斜率.这里k= tanα, α为切线MT的倾角.k 是 函数y=f (x)在x0处的变化率

第三章导数与微分 高等数学少学时 二、导数的定义 定义设y=f(x)在点x的某个邻域内有定义当自变量 在x,处取得增量△x(点x,+△仍在该邻域内)时,相应的函数取 得增量△y=f(x,+△)-f(x,),如果极限 lim Ay=lim fx+△x)-fx) △x-→0△x △x→0 △x 存在,则称函数=f(x)在点x处可导,并称该极限值的函数 在点x处的导数,记'(x),即 f(xa)=lim f(+△)-f(c) △r-→0 △x 北京邮电大学出版社 9
9 二、导数的定义 定义 设 y = f (x) 在 点 x0的某个邻域内有定义,当自变量x 在x0处取得增量x(点 x0 + x 仍在该邻域内 )时 ,相应的函数取 存在,则称函数y = f (x)在 点x0处可导,并称该极限值为函数 在点 x0处的导数,记作f (x0 ),即 ( ) ( ) x f x x f x x y x x + − = → → 0 0 0 0 lim lim ( ) ( ), 0 x0 得增量 y = f x + x − f 如果极限 ( ) ( ) x f x x f x f x x + − = → 0 0 0 0 ( ) lim

第工章导数与微分 高等数学少学时 也可记作y1=, , x=X0 d 导数的定义式也可以写成下面常见的形式 ()=li h-0 +D)-f().(h-A) k,)左m母1飞,K-x,=a x→X0 x-xo imf飞,-小-f()-, h-0 h 北京邮电大学出版社 010
10 | , x x0 y = 也可记作 , 0 x x dx dy = ( ) , 0 x x dx df x = ( ) . 0 x x f x dx d = ( ) ( ) ( ) (h x) h f x h f x f x h = + − = → lim , 0 0 0 0 ( ) ( ) ( ) (x x x) x x f x f x f x x x − = − − = → 0 0 0 0 lim , 0 导数的定义式也可以写成下面常见的形式 ( ) ( ) lim ? 0 0 0 = − − → h f x h f x h