
第一章 函数与极限 高等数学少学时 第二节数列的极限 一、 数列极限的概念 二 数列极限的性质 三、 极限存在准则 北京邮电大学出版社
1 第二节 数列的极限 一、 数列极限的概念 二、 数列极限的性质 三、 极限存在准则

第一章 函数与极限 高等数学少学时 数列极限的概念 我国晋朝时代数学家刘徽 一割圆术依次求出圆内接正 六边形、正十二边形、正二 十四边形,...,正6X2-1 ...边形的面积: A1,A2,…,An)…y 当越大时,正多边形的面 积A就越接近于对应圆的 面积. 北京邮电大学出版社 2
2 一、 数列极限的概念 我国晋朝时代数学家刘徽 , , , , , A1 A2 An ——割圆术依次求出圆内接正 积An 就越 接近于对应圆的 六边形、正十二边形、正二 ……边形的面积: 十四边形,……,正6×2 n-1 当n越大时 ,正多边形的面 面积

第一章 函数与极限 高等数学少学时 定义1设函数xf(是一个以正整数集为定义域的函数, 将其函数值x,n按自变量的大小顺序所排成一列 X13X2,X3),Xn)… ()) 称为数列.数列中的每一个数叫做数列的项,第项x,n叫做数列 的一般项或通项数列(1)简记为{化n}或xm=f(), 例如:0 x=@=a (2)1,2,3,,n,… x,=f(n)=n 3) 123 2 x.f)i 国子1,=1+ 3 n 北京邮电大学出版社 3
3 例如: ( ) n xn f n 1 ( ) , = = 1 , , 3 1 , 2 1 1 1, n 定义1 (2) 1,2,3, ,n, xn = f (n) = n 设函数xn =f (n)是一个以正整数集为定义域的函数, , , , , , (1) x1 x2 x3 xn 称为数列.数列中的每一个数叫做数列的项,第n项xn叫做数列 将其函数值xn按自变量n的大小顺序所排成一列 的一般项或通项.数列(1)简记为{xn }或xn= f (n). ( ) +1 = = n n ( ) , xn f n 1 , , 4 3 , 3 2 , 2 1 3 n + n ( ) ( ) n x f n n n 1 1 − ( ) = = + ( ) , 1 , , 1 4 5 , 3 2 , 2 3 4 0, n n − +

第一章 函数与极限 高等数学少学时 对于给定的数列{x},重要的不是去研究它的每一项如何, 而是要考察当无限增大时它的项的变化趋势观察上面四个数 列,我们发现当→十o∞时,数列(1)的项xn无限接近于常数 0.数列(3)、(4)都与确定的常数1无限接近. 为了进一步理解无限接近的意义,我们来考察数列(4).先 在数轴上依次描出数列中的各项,如图. 3 3 0 2 4 5 X -3 1 5 4 2 北京邮电大学出版社
4 对于给定的数列{xn },重要的不是去研究它的每一项如何, 观察上面四个数 时,数列(1) 的项xn无限接近于常数 为了进一步理解无限接近的意义,我们来考察数列(4).先 而是要考察当n无限增大时它的项的变化趋势. 列,我们发现当 n → + 0.数列(3)、(4)都与确定的常数1无限接近. 在数轴上依次描出数列中的各项,如图. • • • •• • • x 1 2 3 3 2 4 5 • • 5 4 • • • x2 x3 x5 xn x4 0 • 1 x

第一章 函数与极限 高等数学少学时 注意到在数轴上两点的接近程度可以用两点间的距离来描述 因此,要说明“当无限增大时,x,n无限接近1”,只要说明“当n '越大时,xn-1越来越接近于0”. 事实上,由于x,-=,当越来越大时,越来越小,给 定 100当n>100时, 。-=40 即对于第00项以后的所有项心101,X102,七103,…,尤n, 都有x.-1<100成立 北京邮电大学出版社 5
5 xn −1 注意到在数轴上两点的接近程度可以用两点间的距离来描述. 因此,要说明“当n无限增大时,xn无限接近1”,只要说明“当n 越来越大时, 越来越接近于0”. , 1 1 n x 事实上,由于 n − = , 1 当 越来越大时, 越来越小 n n 定 ,当 n 100 时, 100 1 100 1 1 − 1 = n xn . 100 1 都有 xn −1 成立 即对于第100项以后的所有项:x101 , x102 , x103 , , xn , 给

第一章 函数与极限 高等数学少学时 给定 当>1w疏七-云·对于第 1000项以后的所有项:X10013X1002,X1003,“,xn, 客有区,-10),不管ε多么小, 只要n足够大,总能使 x-1=1<e 成立 北京邮电大学出版社 6
6 . 1000 1 都有 xn −1 成立当 n 1000 时, , 1000 1 1 − 1 = n 给定 , xn 1000 1 1000项以后的所有项:x1001, x1002, x1003, , xn , , 这也就是说对于任意给定的正数(即 0),不管 多么小, 即对于第 − = n xn 1 1 只要n足够大,总能使 成立

第一章 函数与极限 高等数学少学时 一般地,对于数列{x}有如下的定义 定义2设{x}为一数列如果存在常数,对于任意给定的正 数£(不论它多么小),总存在正整数N,使得当>N时,不等式 x,-a<8 都成立,那么就称常数a是数列{x}的极限,或称数列化收敛于 a记作 imxn=a或xn→a(n-→o) h-→co 如果这样的常数a不存在,就说数列{x}没有极限,或者说 就说数列x,}是发散的,习惯上也说imxm不存在. 北京邮电大学出版社
7 x a n n = → lim x → a (n → ). 或 n 定义2 x . a , 设 n 为一数列如果存在常数 对于任意给定的正 总存在正整数N,使得当n>N时,不等式 x − a n 一般地,对于数列{xn }有如下的定义. 都成立,那么就称常数a是数列{xn }的极限,或称数列{xn }收敛于 数 (不论它多么小), a.记作 如果这样的常数a不存在,就说数列{xn }没有极限,或者说 就说数列{xn }是发散的,习惯上也说 n 不存在. n x → lim

第一章 函数与极限 高等数学少学时 为了表达方便,引入记号“¥ ” 表示“对于任意给定的”, 号⑨”表示“存在”.于是定义2可以表达为: Ve>0,N>0,当n>N时,恒有xm-d00 例1证明数列2, 子1+,的极限是1 9 证x,-= +-0-1 n e>0,为使上,所以可取正整数v= n 则当n>N时,就有 n+(-1)1- ∞ n 北京邮电大学出版社
8 为了表达方便,引入记号“ ”表示“对于任意给定的”, 记 号“ ”表示“存在”.于是定义2可以表达为: 0, N 0, n N , x a , lim x a. n n n − = → 当 时 恒 有 则 例1 证明数列 1 1 4 3 ( 1) 2, , , , ,1 , 2 3 4 n n − − + 的极限是1. 证 n n n x a n n 1 1 ( 1) 1 − = + − − = − , 1 , 1 0, n n 对 于 为 使 只 需 所以可取正整数 , = 1 N 1 , ( 1) , 1 − + − − n n n N n 则 当 时 就 有 1. ( 1) lim 1 = + − − → n n n n 所以

第一章 函数与极限 5.数列的极限 高等数学少学时 当x=n,则xn=f() lim x =A h-→oo f(n) VA的邻域 A+8 3自然数N 对一切n>N A 相应的点都落 在绿色区域内 A-6 1 23 N4I+2 北京邮电大学出版社
9 当 x = n, 则 x f (n) n = x A n n = → lim 相应的点都落 在绿色区域内 n f(n) 0 A A+ A− 1 2 3 N N+1 N+2 x1 2 x 3 x n x 5. 数列的极限 对一切 n > N 自然数 N A的邻域
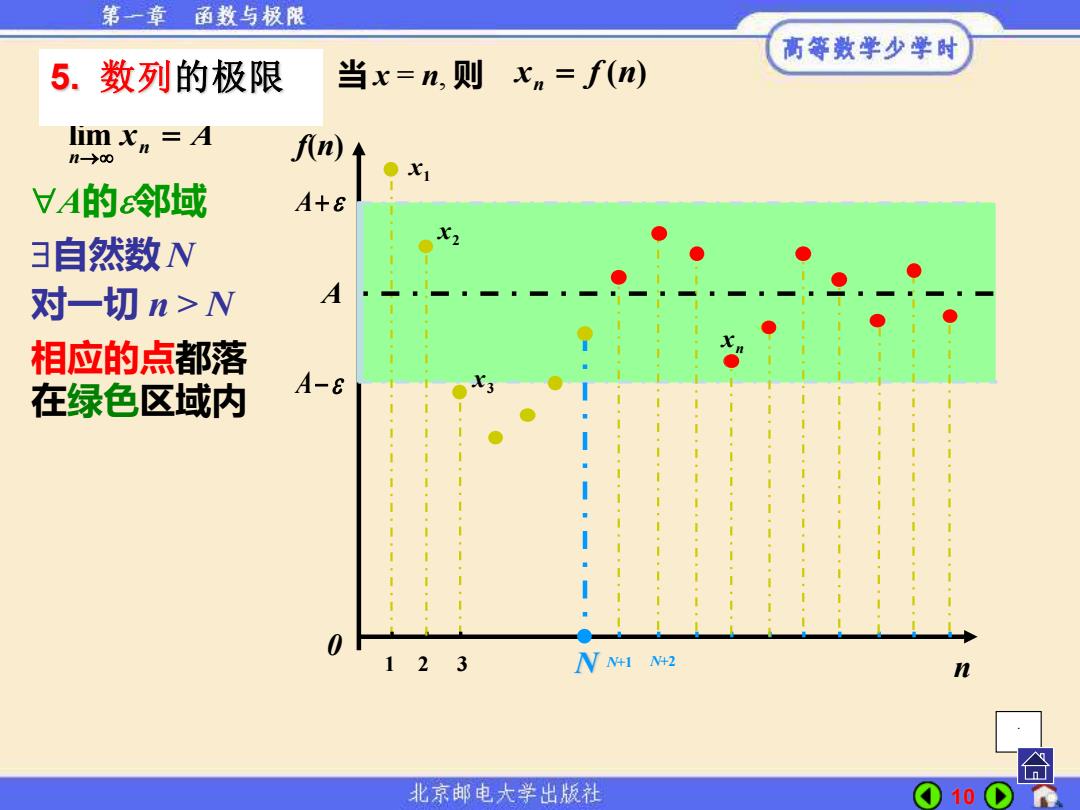
第一章函数与极限 高等数学少学时 5.数列的极限 当x=n,则xn=f(n) limx=A l-→c0 f(n) ●x1 VA的邻域 A+8 3自然数N 对一切n>N A 相应的点都落 在绿色区域内 A-6 1 2 3 N4I+2 北京邮电大学出版社 010
10 当 x = n, 则 x A n n = → lim n f(n) 0 A A+ A− 1 2 3 N N+1 N+2 x1 2 x 3 x x f (n) 5. 数列的极限 n = n x . 相应的点都落 在绿色区域内 对一切 n > N 自然数 N A的邻域