
第二章 矩阵 目录 四 2.1 矩阵的概念 四 2.2 矩阵的运算 四 2.3 逆矩阵 四2.4 矩阵的分块 四2.5 初等变换与初等矩阵 ★2.6 矩阵的秩 四2.7 应用举例 河套大学《线性代数》课件 第二章矩阵 快东学司
第二章 矩 阵 2.1 矩阵的概念 2.2 矩阵的运算 2.3 逆矩阵 2.4 矩阵的分块 2.5 初等变换与初等矩阵 ★ 2.6 矩阵的秩 2.7 应用举例 目录 河套大学《线性代数》课件 第二章 矩阵 快乐学习
本节授裸计划 水人 (2课时) 尚本 必复习 》新课 2.6矩阵的秩 第十五欢课 小结 必思考题及答案提示 必练习、作业及参考答案 河套大学《线性代数》课件 第二章矩阵 快乐学可
快乐学习 以人 为本 ❖复习 ❖新课 2. 6 矩阵的秩 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 十 五 次 课 本节授课计划(2课时) 河套大学《线性代数》课件 第二章 矩阵

水人 2.6 矩阵的秩 尚本 主题调 1.矩阵A的k阶子式 2.矩阵A的秩 3.满秩矩阵 4.降秩矩阵, 返回 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 为本 主 题 词 2.6 矩阵的秩 河套大学《线性代数》课件 第二章 矩阵 1.矩阵 的 阶子式 2.矩阵 的秩 3.满秩矩阵 4.降秩矩阵. A A k 返回

相吴内容国预 水人 尚本 矩阵阶梯形、最简形以及标准的概念 123 2 100 2 100 07 5 01 5 01 00 -13 -14 00 14 0 0 0 0 0 0 本节课主要介绍矩阵的秩的概念及其求法, 河套大学《线性代数》课件 第二章矩阵 快东骨司
快乐学习 以人 相关内容回顾 为本 河套大学《线性代数》课件 第二章 矩阵 矩阵阶梯形、最简形以及标准的概念. 本节课主要介绍矩阵的秩的概念及其求法. − − 0 0 0 0 0 0 13 14 0 7 7 5 1 2 3 2 − 0 0 0 0 0 0 1 14 0 1 0 5 1 0 0 2 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 , ,

水人 新课 2.6矩阵的秩 尚本 我们知道,给定一个mxn矩阵A,它的标准形 D mxn 由数r完全确定.这个数也就是矩阵A的行阶梯形 中非零行的行数,这个数便是矩阵A的秩.但由于 这个数的唯一性尚未证明,因此下面我们用另 个说法给出矩阵秩的定义 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.6 矩阵的秩 为本 河套大学《线性代数》课件 第二章 矩阵 新课 我们知道,给定一个 mn 矩阵 A ,它的标准形 m n r O O E O D = 由数 r 完全确定.这个数也就是矩阵 A 的行阶梯形 中非零行的行数,这个数便是矩阵 A 的秩. 但由于 这个数的唯一性尚未证明,因此下面我们用另一 个说法给出矩阵秩的定义

水人 新课 2.6矩阵的秩 (续1) 尚本 定义2.6.在m×n 矩阵A中,任取k行与人 列亿≤m,k<,位于这些行列交叉处的2个元 素,不改变它们在A中所处的位置次序而得的 阶行列式称为矩阵A的k阶子式. 注意,矩阵的k阶子式是行列式而不是矩阵; mxn 矩阵A的k阶子式共有C·C个, 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.6 矩阵的秩 (续1) 为本 河套大学《线性代数》课件 第二章 矩阵 新课 定义2.6.1 在 mn 矩阵 A 中,任取 k 行与 k 列 (k m,k n) ,位于这些行列交叉处的 2 k 个元 素,不改变它们在 中所处的位置次序而得的 阶行列式称为矩阵 的 阶子式. A k A k 注意:矩阵的 k 阶子式是行列式而不是矩阵; mn 矩阵 A 的 k 阶子式共有 k n k Cm C 个

水人 新课 2.6 矩阵的秩(续2) 尚本 定义2.6.2 设在矩阵A中有一个不等于0的”阶 子式D,且所有r+1阶子式((若存在)全等于0, 则称D为矩阵A的最高阶非零子式,称r为矩阵 4的秩,记作(4=r,并规定零矩阵的秩等于0. 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.6 矩阵的秩 (续2) 为本 河套大学《线性代数》课件 第二章 矩阵 新课 定义2.6.2 设在矩阵 A 中有一个不等于0的 r 子式 阶 D ,且所有 r +1 则称 D 为矩阵 A 的最高阶非零子式,称 r 为矩阵 A 的秩,记作 R(A) = r .并规定零矩阵的秩等于0. 阶子式(若存在)全等于0

水人 新课 2.6矩阵的秩 (续3) 尚本 由行列式的性质可知,在矩阵A中当所有r+1 阶子式全等于0时,所有高于+阶的子式也全为0 因此把阶非零子式称为最高阶非零子式,并由此 可知矩阵A的最高阶非零子式可能不止一个.而A 的秩(④就是A的非零子式的最高阶数 滋定义26.2表明:若矩阵A中有一个阶非零子 式,则(≥:若A中所有r阶子式全为0,则R(④<r 河套大学《线性代数》课件 第二章矩阵 快乐骨司
的最高阶非零子式可能不止一个.而 中所有 快乐学习 以人 2.6 矩阵的秩 (续3) 为本 河套大学《线性代数》课件 第二章 矩阵 新课 由行列式的性质可知,在矩阵 A 中当所有 r +1 阶子式全等于0时,所有高于 r +1 阶的子式也全为0 因此把 r 阶非零子式称为最高阶非零子式,并由此 可知矩阵 A A 的秩 R(A) 就是 A 的非零子式的最高阶数. 定义2.6.2表明:若矩阵 A 中有一个 r 阶非零子 式,则 R(A) r; 若 A r 阶子式全为0,则 R(A) r. 注

水人 新课 2.6矩阵的秩 (续4) 尚本 显然,若矩阵A为mxn矩阵,则Rsm,R④sn 对于n阶矩阵A,若4≠0,则R(④=n;若0 则④<n因此,可逆矩阵又称满秩矩阵, 不可逆 矩阵(奇异矩阵)又称降秩矩阵, 由于行列式与其转置行列式相等,因此,矩阵 的子式与A的子式对应相等,从而(4)=(④ 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.6 矩阵的秩 (续4) 为本 河套大学《线性代数》课件 第二章 矩阵 新课 ;若 显然,若矩阵 A 为 mn 矩阵,则 R(A) m,R(A) n. 对于 n 阶矩阵 A ,若 | A | 0 ,则 R(A) = n | A |= 0 则 R(A) n 因此,可逆矩阵又称满秩矩阵,不可逆 矩阵(奇异矩阵)又称降秩矩阵. 由于行列式与其转置行列式相等,因此,矩阵 T A 的子式与 A 的子式对应相等,从而 R(A ) R(A) T =
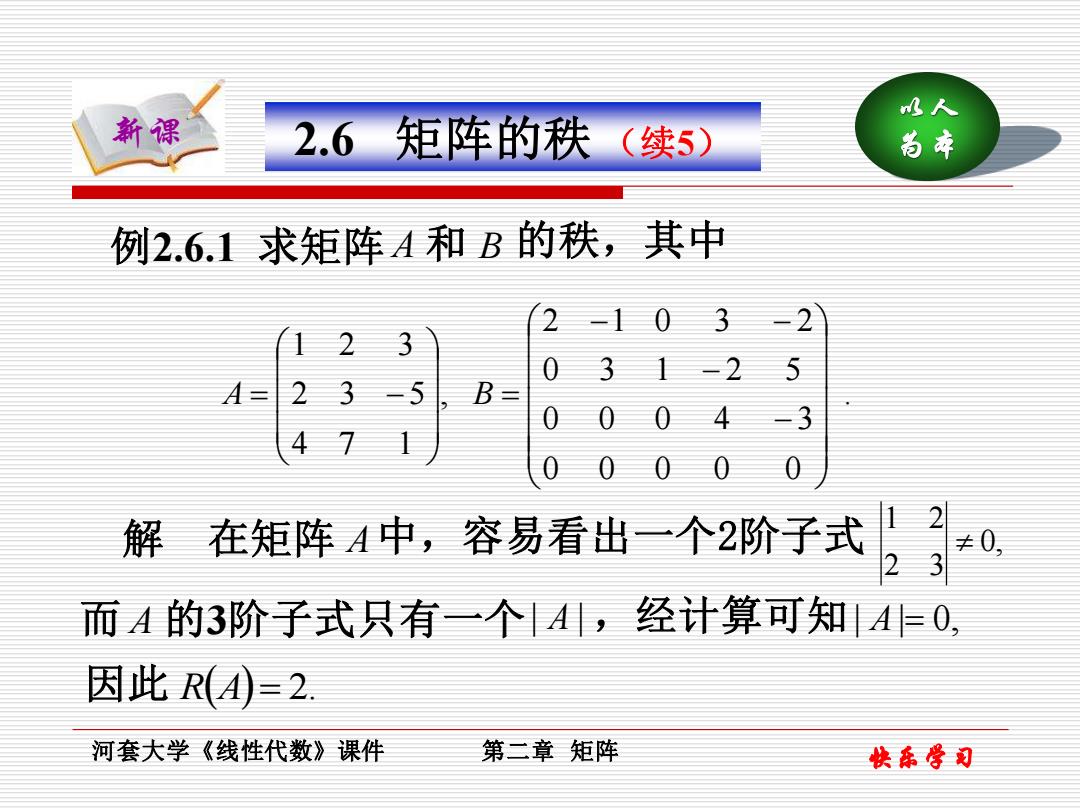
水人 新课 2.6矩阵的秩 (续5) 尚本 例2.6.1求矩阵A和B的秩,其中 2-103-2 123 031-25 A=23-5 B= 0 004-3 47 00 0 0 0 解 在矩阵A中,容易看出一个2阶子式 ≠0 而A的3阶子式只有一个,经计算可知A0, 因此R(A-2 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 2.6 矩阵的秩 (续5) 为本 河套大学《线性代数》课件 第二章 矩阵 新课 例2.6.1 求矩阵 A 和 B 的秩,其中 . 0 0 0 0 0 0 0 0 4 3 0 3 1 2 5 2 1 0 3 2 , 4 7 1 2 3 5 1 2 3 − − − − = A = − B 解 在矩阵 A 中,容易看出一个2阶子式 0, 2 3 1 2 而 A 的3阶子式只有一个 | A | ,经计算可知 | A |= 0, 因此 R(A) = 2