
第三章 微分中值定理与导数的应用 高等数学少学时 第三章微分中值交理 与导数的爱用 第一节 微分中值定理 第二节 洛必达法则 第三节 泰勒公式 第四节 函数的单调性与曲线的凹凸性 第五节 函数的极值与最大值最小值 第六节 方程的近似解 北京邮电大学出版社
1 第一节 微分中值定理 第三章 微分中值定理 第二节 洛必达法则 第三节 泰勒公式 第四节 函数的单调性与曲线的凹凸性 第五节 函数的极值与最大值最小值 第六节 方程的近似解 与导数的应用

第三章 微分中值定理与导数的应用 高等数学少学时 第一节微分中值定理 一、罗尔(RolIe)定理 二、拉格朗日(Lagrange)中值定理 三、柯西(Cauchy)中值定理 北京邮电大学出版社
2 一、罗尔(Rolle)定理 二、拉格朗日(Lagrange)中值定理 三、柯西(Cauchy)中值定理 第一节 微分中值定理

第三章微分中值定理与导数的应用 高等数学少学时 一、罗尔(Rolle)定理 fx)满足: B (1)在区间[a,b]上连续; A (2)在区间(a,b)内可导; a (3)f(M)=f(b), >在(a,b)内至少存在一点5,使f'(5)=0. 证因为f(x)在[a,b]上连续,故在[a,b]上取得最大值M 和最小值m. 若M=m,则f(x)≡M,x∈[a,b], 因此5∈(a,b),f'()=0. 北京邮电大学出版社 03
3 一、罗尔(Rolle)定理 f (x)满足: (1) 在区间 [a , b] 上连续; (2) 在区间 (a , b) 内可导; (3) f ( a ) = f ( b ), 证 故在 [a , b] 上取得最大值 M 和最小值 m . 若 M = m , 则 因此 在( a , b ) 内至少存在一点 因为 f (x) 在 [a, b] 上连续, y O a b A B C x f x M x a b ( ) , [ , ] , ,使f ( ) = 0

第三章 微分中值定理与导数的应用 高等数学少学时 若M>m,则M和m中至少有一个与端点值不等, 不妨设M≠f(a),则至少存在一点5∈(a,b),使 f(5)=M,下面证明f'(E)=0. y 因为f(x)在5∈(a,b)处可导,所以 B A f(5)=lim f(5+△x)-f(5) △x0 △x a =∫f≥0(4x→0) =f5)≤0(ax→0) >f'(5)=0. 北京邮电大学出版社
4 若 M > m , 则 不妨设 则至少存在一点 使 下面证明 因为 f x( ) 在 处可导, 所以 M 和 m 中至少有一个与端点值不等, y O a b A B C x M f a ( ) , ( , ), a b f M ( ) , = f ( ) 0. = ( 0 ) x − → 0 ( 0 ) x + → f ( ) 0. =
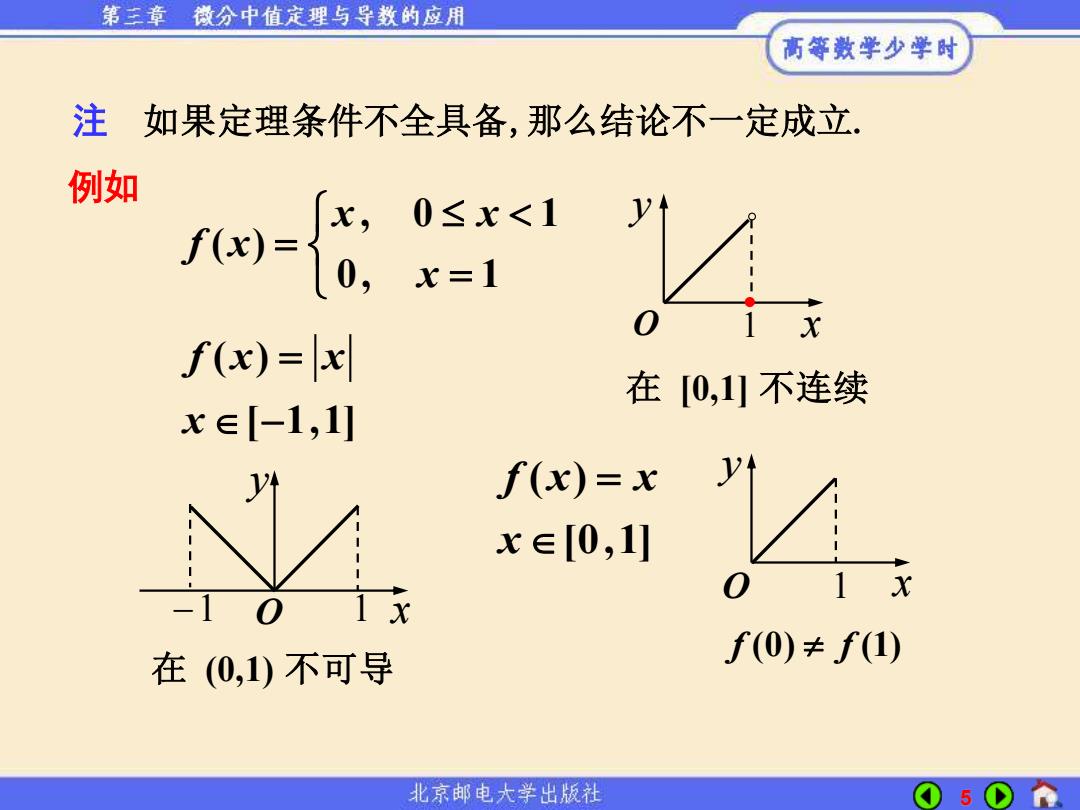
第三章微分中值定理与导数的应用 高等数学少学时 注如果定理条件不全具备,那么结论不一定成立 例如 x,0≤x<1 f)={0,x=1 f(x)=x 在[0,1山不连续 x∈[-1,1] f(x)=x y x∈[0,1] 0 X 1 x 在(0,1)不可导 北京邮电大学出版社 5
5 注 如果定理条件不全具备,那么结论不一定成立. 例如 在 [0,1] 不连续 1 x y −1 O 1 x y O f f (0) (1) 1 x y O 在 (0,1) 不可导 , 0 1 ( ) 0, 1 x x f x x = = ( ) [ 1,1] f x x x = − ( ) [0,1] f x x x =

第三章 微分中值定理与导数的应用 高等数学少学时 例1不用求出f(x)=(x-1)(x-2)x-3)(x-4)的导数,说明 方程f'(x)=0有几个实根,并指出它们所在的区间. 解函数f(x)是实数域上的初等函数,在闭区间[1,2]上连续, 在开区间(1,2)内可导,且f(1)=f(2)=0.故由罗尔定理可知, 在开区间(1,2)内至少存在一点x使得f"'(c)=0. 同理可知,在开区间(2,3)内至少存在一点x2,在开区间 3,4)内至少存在一点3,使得f"(2)=f')=0又因为f)=0 是一元三次代数方程,所以至多有三个实根.因此f'(x)=0有 三个实根,分别在开区间(1,2)、(2,3)、3,4)内. 北京邮电大学出版社
6 同理可知,在开区间(2,3)内至少存在一点x2 ,在开区间 (3,4)内至少存在一点x3 ,使得f '(x2 )=f '(x3 ) = 0. 方程 f x ( ) 0 = 有几个实根,并指出它们所在的区间. 解 故由罗尔定理可知, 是一元三次代数方程, 所以至多有三个实根. 三个实根,分别在开区间(1,2)、(2,3)、(3,4)内. 函数 f (x)是实数域上的初等函数,在闭区间[1,2]上连续, 在开区间(1,2)内可导,且f (1)=f (2)=0. 例1 不用求出 f x x x x x ( ) ( 1)( 2)( 3)( 4) = − − − − 的导数,说明 在开区间(1,2)内至少存在一点x1使得f '(x1 ) = 0. 又因为f '(x) = 0 因此f '(x) = 0有

第三章 微分中值定理与导数的应用 高等数学少学时 二、拉格朗日中值定理 条件:若f(x在[a,b上连续, f(x)在(,b)内可导. 如右图所示,在直角坐标系 xOy中,曲线弧AB所表示的 函数f(x)满足罗尔定理中的 b x 条件(1)(2),但条件(3)不满足.我们把坐标系xOy旋转到 uOv的位置,使得Ou轴平行于弦AB,那么在直角坐标系 uOv中,弧AB是光滑的且两端点的纵坐标相等.根据罗尔 定理的几何意义可知,在弧AB上至少有一点C(5,f() 处的切线平行于O轴,从而点C处的切线是平行于弦 AB的.即f'(5)=()-f(@ b-a 北京邮电大学出版社
7 二、拉格朗日中值定理 若f (x)在a,b上连续, f x( ) 条件: 在 ( , ) a b 内可导. O B C a b u y v A x 如右图所示, xOy 中,曲线弧 AB 所表示的 在直角坐标系 函数 f x( ) 满足罗尔定理中的 条件(1)(2),但条件(3)不满足. 我们把坐标系 xOy 旋转到 uOv 的位置,使得 Ou 轴平行于弦 AB ,那么在直角坐标系 uOv 中,弧 AB 是光滑的且两端点的纵坐标相等. 定理的几何意义可知,在弧 AB 上至少有一点 C ( , f ( )) 处的切线平行于 Ou 轴, 从而点 C 处的切线是平行于弦 AB 的. 根据罗尔 ( ) ( ) ( ) . f b f a f b a − = − 即

第三章微分中值定理与导数的应用 高等数学少学时 拉格朗日中值定理 y=f(x)满足: (1)在区间[a,b]上连续; B (2)在区间(a,b)内可导, >至少存在一点5∈(M,b), 使f(b)-f(a)=f'(5)(b-).(1) 定理中的(1)式叫做拉格朗日中值公式。 令a=x,b=x+△x,则 △y=f'(x+8△x)△x(0<8<1) (2) 5 公式(2)叫做有限增量公式 北京邮电大学出版社
8 拉格朗日中值定理 (1) 在区间 [ a , b ] 上连续; 满足: (2) 在区间 ( a , b ) 内可导, 至少存在一点 使 f b f a f b a ( ) ( ) ( )( ) . − = − (1) 定理中的(1)式叫做拉格朗日中值公式. = + y f x x x ( ) (0 1) 令 则 (2) 公式(2)叫做有限增量公式. O B C a b u y v A x y f x = ( ) ( , ) , a b

第三章 微分中值定理与导数的应用 高等数学少学时 推论:若函数f(x)在区间I上满足f'(x)=0,则f(x) 在I上必为常数. 证在1上任取两点x1,心2(x1<x2),在【x,]上应用拉 格朗日中值公式,得 f(x2)-f(x)=f(5)x2-x)=0 (X1<5<X2) .f(x2)=f(x) 由1,x2的任意性知,f(x)在I上为常数. 结合第二章中常数的导数公式,有下面的结论: 函数f(x)在区间I上为常数的充分必要条件是f(x)在区间I 上的导数恒等于零. 北京邮电大学出版社 9
9 推论: 若函数 在区间 I 上满足 则 在 I 上必为常数. 证 在 I 上任取两点 格朗日中值公式, 得 由 的任意性知, 在 I 上为常数. 结合第二章中常数的导数公式,有下面的结论: 函数 f (x) 在区间 I 上为常数的充分必要条件是 f (x) 在区间 I 上的导数恒等于零. 在 [ x1 , x2 ] 上应用拉 f x( ) f x ( ) 0, f x( ) 2 1 = − f x x ( )( ) = 0 1 2 ( ) x x 2 1 = f x f x ( ) ( )

第三章 微分中值定理与导数的应用 高等数学少学时 元 例2 证明arctanx+arccotx= 2 证设f(r)=arctanx+arccotx,则对于任意x∈(-oo,+oo) f(x)= 1 1 +x21+x=0 由推论得f(x)=C. 又f0=2,所以对于任意xe(0,+o), arctanx+arccotx= 2 北京邮电大学出版社 10
10 例2 证明 arctan arccot . 2 x x + = 证 设 f x x x ( ) arctan arccot = + , 则对于任意 x − + ( , ) 2 2 1 1 ( ) 0 1 1 f x x x =−= + + 由推论得 f x C ( ) . = 又 (1) , 2 f = 所以对于任意 x − + ( , ,) arctan arccot . 2 x x + =