
第三章微分中值定理与导数的应用 高等数学少学时 第六节方程的近仙解 一、二分法 二、切线法 北京邮电大学出版社 10
1 第六节 方程的近似解 一、二分法 二、切线法

第三章 微分中值定理与导数的应用 高等数学少学时 一、二分法 设f(x)在[a,b]上连续,f(a)f(b)<0,且方程f(x)=0 在(a,b)内仅有一个实根5,则区间[a,]称为根5的隔离 区间.下面用二分法求根5的近似值. (取a,1的中点5=主,计算(5)若f(5)=0, 2 则51即为方程的根5.否则进行下一步. (2)若f(@)f(5)<0,则方程f(x)=0的根5在(a,5) 内,此时取a,]为根的新隔离区间;同样若f()f(b)<0, 则取[5,b]为根的新隔离区间. 北京邮电大学出版社
2 一、二分法 设 f x( ) 在 a b, 上连续, f a f b ( ) ( ) 0, 且方程 f x( ) = 0 在 (a b, ) 内仅有一个实根 , 则区间 [a , b] 称为根 的隔离 区间. 下面用二分法求根 的近似值. (1) 取 [a , b] 的中点 1 , 2 a b + = 计算 f ( 1 ). 若 f ( 1 ) = 0, 则 1 即为方程的根 . 否则进行下一步. (2) 若 f a f ( ) ( 1 ) 0, 则方程 f x( ) = 0 的根 在 ( ) 1 a, 内, 此时取 1 a, 为根的新隔离区间;同样若 ( ) ( ) 1 f f b 0, 则取 ,b 1 为根的新隔离区间

第三章 微分中值定理与导数的应用 高等数学少学时 将根的新隔离区间记灯a,4]则么-4=(6-): 重复上述做法,当5≠5=马十么时,可求得4,<5<6, 2 且6-4=是(6-小. 如此重复n次,可求得,<专<,且6,-,=(-小 若用“。或6,近似代替5其误差小于(b-) 北京邮电大学出版社 3
3 将根的新隔离区间记为 1 1 a b, , 则 ( ) 1 1 1 . 2 b a b a − = − 重复上述做法,当 1 1 2 2 a b + = 时, 可求得 2 2 a b 且 ( ) 2 2 2 1 . 2 b a b a − = − 如此重复 n 次, 可求得 , n n a b 且 ( ) 1 . 2 n n n b a b a − = − 若用 n a 或 n b 近似代替 其误差小于 ( ) 1 . 2 n b a −

第三章 微分中值定理与导数的应用 高等数学少学时 二、切线法 设f(x)在[a,b]上具有二阶导数,f(a)f(b)0(b)f(a)>0,f(b)0,f"(x)>0f'(x)0 北京邮电大学出版社
4 二、切线法 设 f x( ) 在 a b, 上具有二阶导数, f a f b ( ) ( ) 0 且 f x ( ) 及 f x ( ) 在 a b, 上保持定号. 在上述条件下, 方程 f x( ) = 0 在 (a b, ) 内有唯一的实根 , a b, 为根的一个隔离区间.此时, y f x = ( ) 在 a b, 上的图形 AB 只有如下图所示的四种不同情形. x y O A B a b x1 x y O A B a b x1 ( ) ( ) ( ) 0, ( ) 0 ( ) 0, 0 f x f x a f a f b ( ) ( ) ( ) 0, ( ) 0 ( ) 0, 0 f x f x b f a f b

第三章微分中值定理与导数的应用 高等数学少学时 B (c)f(a)0 (df(a)>0,f(b)0,f"(x)<0 f'(x)<0,f"(x)<0 考虑用曲线弧一端的切线来代替曲线弧,从而求出 方程实根的近似值,这种方法叫做切线法 从上面图(-(b)中看出,如果在纵坐标与"(x) 同号的那个端点(记作(x,f(x))作切线,这切线与x 轴的交点的横坐标x1就比x更接近方程的根5. 北京邮电大学出版社 5
5 x y O A B a b x1 x y O A B a b x1 ( ) ( ) ( ) 0, ( ) 0 ( ) 0, 0 f x f x c f a f b ( ) ( ) ( ) 0, ( ) 0 ( ) 0, 0 f x f x d f a f b 考虑用曲线弧一端的切线来代替曲线弧,从而求出 方程实根的近似值,这种方法叫做切线法. 从上面图(a)-(b)中看出,如果在纵坐标与 f x ( ) 同号的那个端点(记作 ( x f x 0 0 , ( )) )作切线,这切线与x 轴的交点的横坐标x1 就比x0更接近方程的根
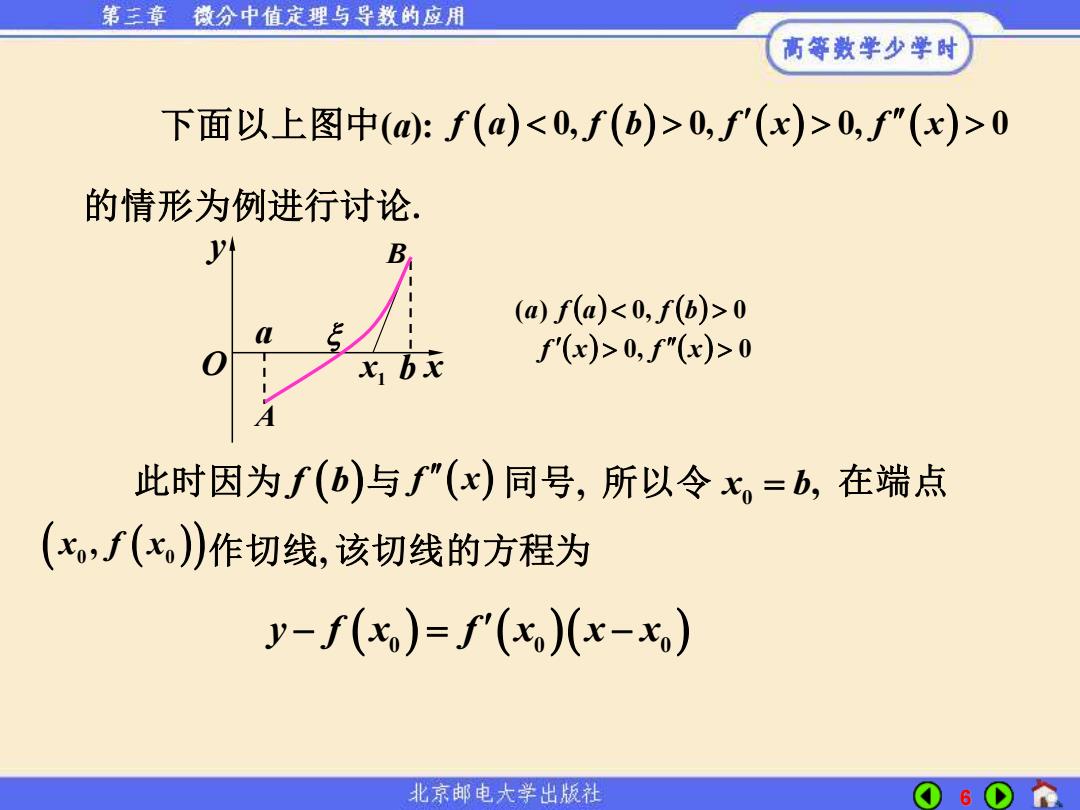
第三章 微分中值定理与导数的应用 高等数学少学时 下面以上图中(:f(a)0,f'(x)>0,f"(x)>0 的情形为例进行讨论. B ()f(a)0 七1bx f'(x)>0,f"(x)>0 此时因为f(b)与f"(x)同号,所以令x。=b,在端点 x,f(x)作切线,该切线的方程为 y-f(x)=f(x)(x-xo) 北京邮电大学出版社 6
6 下面以上图中(a): f a f b f x f x ( ) 0, 0, 0, 0 ( ) ( ) ( ) 的情形为例进行讨论. ( ) ( ) ( ) 0, ( ) 0 ( ) 0, 0 f x f x a f a f b x y O A B a b x1 此时因为 f b( ) 与 f x ( ) 同号, 所以令 0 x b = , 在端点 ( x f x 0 0 , ( )) 作切线, 该切线的方程为 y f x f x x x − = − ( 0 0 0 ) ( )( )

第三章 微分中值定理与导数的应用 高等数学少学时 令y=0,从上式中解出x,就得到切线与x轴交点的横坐标为 f(x) x=x-f(x】 它比x,更接近方程的根5.再在点(,f(x)作切线, 可得根的近似值飞,.如此继续,一般地,在点(xf(xi) 作切线,得根的近似值 f(xi) x=x-f) (1) 如果f()与f"(x)同号,切线作在端点A(如情形 (b)及(c)),可记x=4,仍按公式(1)计算切线与x轴 交点的横坐标. 北京邮电大学出版社
7 令 y=0,从上式中解出x , 就得到切线与x轴交点的横坐标为 ( ) ( ) 0 1 0 0 , f x x x f x = − 它比 0 x 更接近方程的根 . 再在点 ( x f x 1 1 , ( )) 作切线, 作切线,得根的近似值 ( ) ( ) 1 1 1 . n n n n f x x x f x − − − = − (1) 如果 f (a) 与 f x ( ) 同号,切线作在端点 A (如情形 ( b ) 及 ( c ) ) , 可记 0 x a = , 仍按公式(1)计算切线与x轴 交点的横坐标. 可得根的近似值 . 如此继续,一般地,在点 ( x f x n n − − 1 1 , ( )) 2 x

第三章微分中值定理与导数的应用 高等数学少学时 小结 寻求方程根近似值的方法 一、二分法 二、切线法 f(x) X=xf) 北京邮电大学出版社
8 小 结 一、二分法 二、切线法 ( ) ( ) 1 1 1 . n n n n f x x x f x − − − = − 寻求方程根近似值的方法