运城学院：《复变函数论 Theory of Functions of Complex Variable》课程教学资源（教学大纲，数学与应用数学）

1.9《复变函数论》教学大纲 一、课程基本信息 课程编码：0601112B 中文名称：复变函数论 英文名称：Theory of Functions of Complex Variable 课程类别：专业基础及核心课 总学时：48 总学分：3 适用专业：数学与应用数学 先修课程：数学分析，高等代数，解析几何 二、课程目标 (一)具体目标 通过本课程的学习，使学生达到以下目标： 1.了解复变函数的发展历史，遵循周易中的复卦的复。【支撑毕业要求1】 2.理解复数的表示方法。【支撑半业要求2】 3理解复变函数的基本概念、基本理论、基本方法。【支撑半业要求3】 4掌握留数的计算和应用。【支撑毕业要求5】 5能够应用复变函数方法解决实际问题，理解不同学科间的联系与渗透。【支撑 毕业要求3、4】 6培养了抽象思维能力、逻辑推理能力、空间想象能力、科学计算能力及分析和 解决实际问题的能力。【支撑半业要求4、6、7、8】 (二)课程目标与毕业要求的对应关系 表1课程目标与毕业要求的对应关系 课程目标 支撑的毕业要求 支撑的毕业要求指标点 1-1以立德树人为根本，以教书有人为己任。遵守中学教师职 课程目标1 1.师德规范 业道德规范，具有依法执教意识，立志成为有理想信念、有道

1.9 《复变函数论》教学大纲 一、课程基本信息 课程编码：0601112B 中文名称：复变函数论 英文名称：Theory of Functions of Complex Variable 课程类别：专业基础及核心课 总 学 时：48 总 学 分：3 适用专业：数学与应用数学 先修课程：数学分析，高等代数，解析几何 二、课程目标 （一）具体目标 通过本课程的学习，使学生达到以下目标： 1. 了解复变函数的发展历史，遵循周易中的复卦的复。【支撑毕业要求 1】 2. 理解复数的表示方法。【支撑毕业要求 2】 3.理解复变函数的基本概念、基本理论、基本方法。【支撑毕业要求 3】 4.掌握留数的计算和应用。【支撑毕业要求 5】 5.能够应用复变函数方法解决实际问题，理解不同学科间的联系与渗透。【支撑 毕业要求 3、4】 6.培养了抽象思维能力、逻辑推理能力、空间想象能力、科学计算能力及分析和 解决实际问题的能力。【支撑毕业要求 4、6、7、8】 （二）课程目标与毕业要求的对应关系 表 1 课程目标与毕业要求的对应关系 课程目标 支撑的毕业要求 支撑的毕业要求指标点 课程目标 1 1.师德规范 1-1 以立德树 人为根本，以教书育人为己任。遵守中学教师职 业道德规范，具有依法执教意识， 立志成为有理想信念、有道

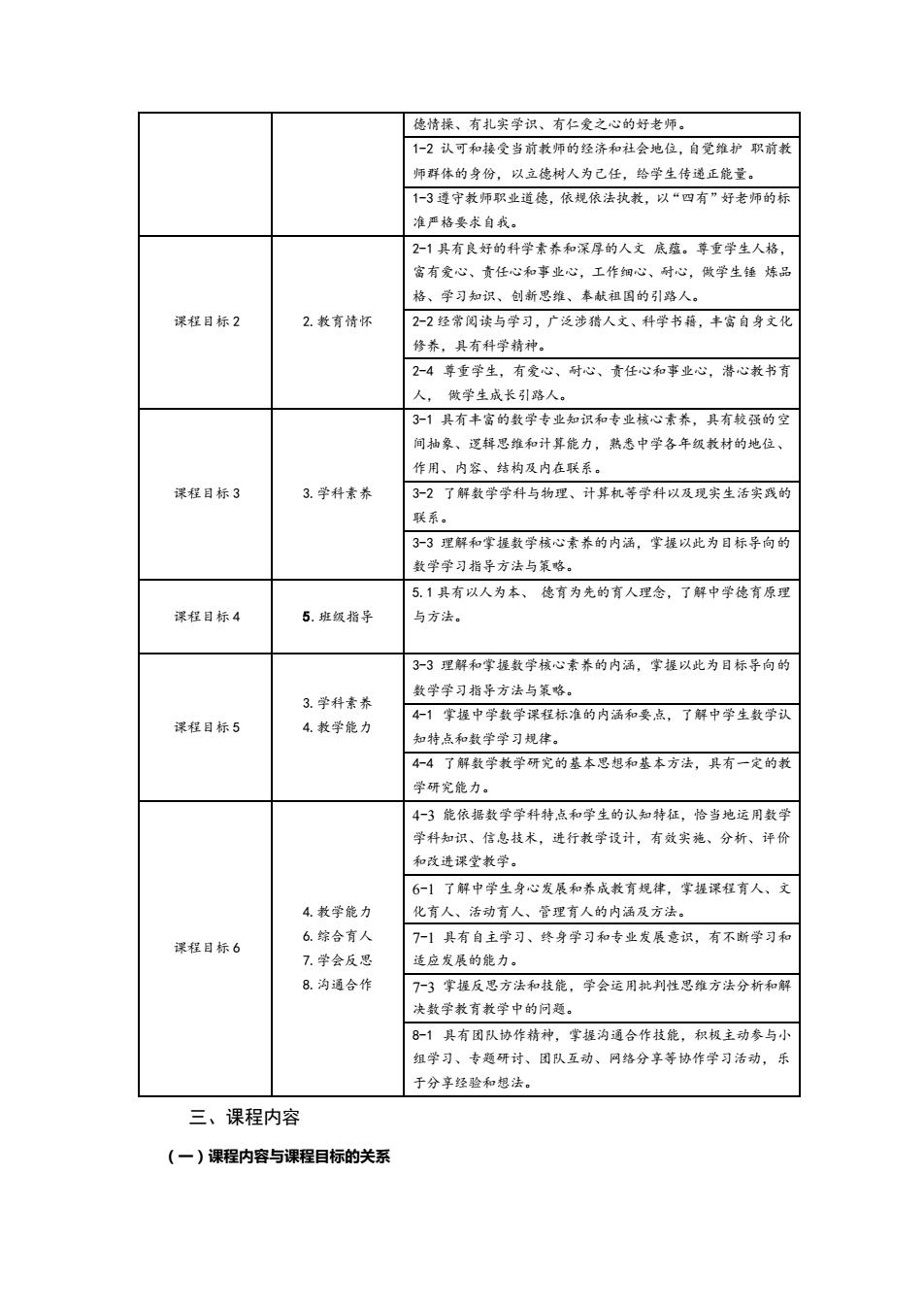
德情揉、有扎实学识、有仁爱之心的好老师。 1-2认可和接受当前教师的经济和社会地位，自觉维护职前教 师群体的身份，以立德树人为己任，给学生传递正能量。 1-3遵守教师职业道德，依规依法执教，以“四有”好老师的标 准严格要求自我。 2-1具有良好的科学素养和深厚的人文底蕴。尊重学生人格， 富有爱心、责任心和事业心，工作细心、耐心，做学生锤炼品 格、学习知识、创新思维、奉献祖国的引路人。 课程目标2 2.教有情怀 2-2经常阅读与学习，广泛涉猎人文、科学书籍，丰富自身文化 修养，具有科学精神。 2-4尊重学生，有爱心、耐心、责任心和事业心，潜心教书有 人，做学生成长引路人。 3-1具有丰富的数学专业知识和专业核心素养，具有较强的空 间抽象、逻辑思维和计算能力，熟悉中学各年级教材的地位、 作用、内容、结构及内在联系。 课程目标3 3.学科素养 3-2了解数学学科与物理、计算机等学科以及现实生活实践的 联系。 3-3理解和掌提数学核心素养的内涵，掌提以此为目标导向的 数学学习指导方法与策略。 5.1具有以人为本、德有为先的有人理念，了解中学德育原理 课程目标4 5.班级指导 与方法。 33理解和掌提数学核心素养的内涵，掌提以此为目标导向的 数学学习指导方法与策略。 3.学科素养 4-1掌握中学数学课程标准的内涵和要点，了解中学生数学认 课程目标5 4.教学能力 知特点和数学学习规律。 4-4了解数学教学研究的基本思想和基本方法，具有一定的教 学研究能力。 4-3能依据数学学科特点和学生的认知特征，恰当地运用数学 学科知识、信息技术，进行教学设计，有效实施、分析、评价 和改进课堂教学。 6-1了解中学生身心发展和养成教有规律，掌提课程有人、文 4.教学能力 化有人、活动有人、管理有人的内涵及方法。 课程目标6 6.综合育人 7-1具有自主学习、终身学习和专业发展意识，有不断学习和 7.学会反思 适应发展的能力。 8.沟通合作 T-3掌提反思方法和技能，学会运用批判性思维方法分析和解 决数学教育教学中的问题。 8-1具有团队协作精神，掌提沟通合作技能，积极主动参与小 组学习、专题研讨、团队互动、网络分享等协作学习活动，乐 于分享经验和想法。 三、课程内容 (一)课程内容与课程目标的关系

德情操、有扎实学识、有仁爱之心的好老师。 1-2 认可和接受当前教师的经济和社会地位，自觉维护 职前教 师群体的身份，以立德树人为己任，给学生传递正能量。 1-3 遵守教师职业道德，依规依法执教，以“四有”好老师的标 准严格要求自我。 课程目标 2 2.教育情怀 2-1 具有良好的科学素养和深厚的人文 底蕴。尊重学生人格， 富有爱心、责任心和事业心，工作细心、耐心，做学生锤 炼品 格、学习知识、创新思维、奉献祖国的引路人。 2-2 经常阅读与学习，广泛涉猎人文、科学书籍，丰富自身文化 修养，具有科学精神。 2-4 尊重学生，有爱心、耐心、责任心和事业心，潜心教书育 人， 做学生成长引路人。 课程目标 3 3.学科素养 3-1 具有丰富的数学专业知识和专业核心素养，具有较强的空 间抽象、逻辑思维和计算能力，熟悉中学各年级教材的地位、 作用、内容、结构及内在联系。 3-2 了解数学学科与物理、计算机等学科以及现实生活实践的 联系。 3-3 理解和掌握数学核心素养的内涵，掌握以此为目标导向的 数学学习指导方法与策略。 课程目标 4 5.班级指导 5.1 具有以人为本、 德育为先的育人理念，了解中学德育原理 与方法。 课程目标 5 3.学科素养 4.教学能力 3-3 理解和掌握数学核心素养的内涵，掌握以此为目标导向的 数学学习指导方法与策略。 4-1 掌握中学数学课程标准的内涵和要点，了解中学生数学认 知特点和数学学习规律。 4-4 了解数学教学研究的基本思想和基本方法，具有一定的教 学研究能力。 课程目标 6 4.教学能力 6.综合育人 7.学会反思 8.沟通合作 4-3 能依据数学学科特点和学生的认知特征，恰当地运用数学 学科知识、信息技术，进行教学设计，有效实施、分析、评价 和改进课堂教学。 6-1 了解中学生身心发展和养成教育规律，掌握课程育人、文 化育人、活动育人、管理育人的内涵及方法。 7-1 具有自主学习、终身学习和专业发展意识，有不断学习和 适应发展的能力。 7-3 掌握反思方法和技能，学会运用批判性思维方法分析和解 决数学教育教学中的问题。 8-1 具有团队协作精神，掌握沟通合作技能，积极主动参与小 组学习、专题研讨、团队互动、网络分享等协作学习活动，乐 于分享经验和想法。 三、课程内容 （一）课程内容与课程目标的关系

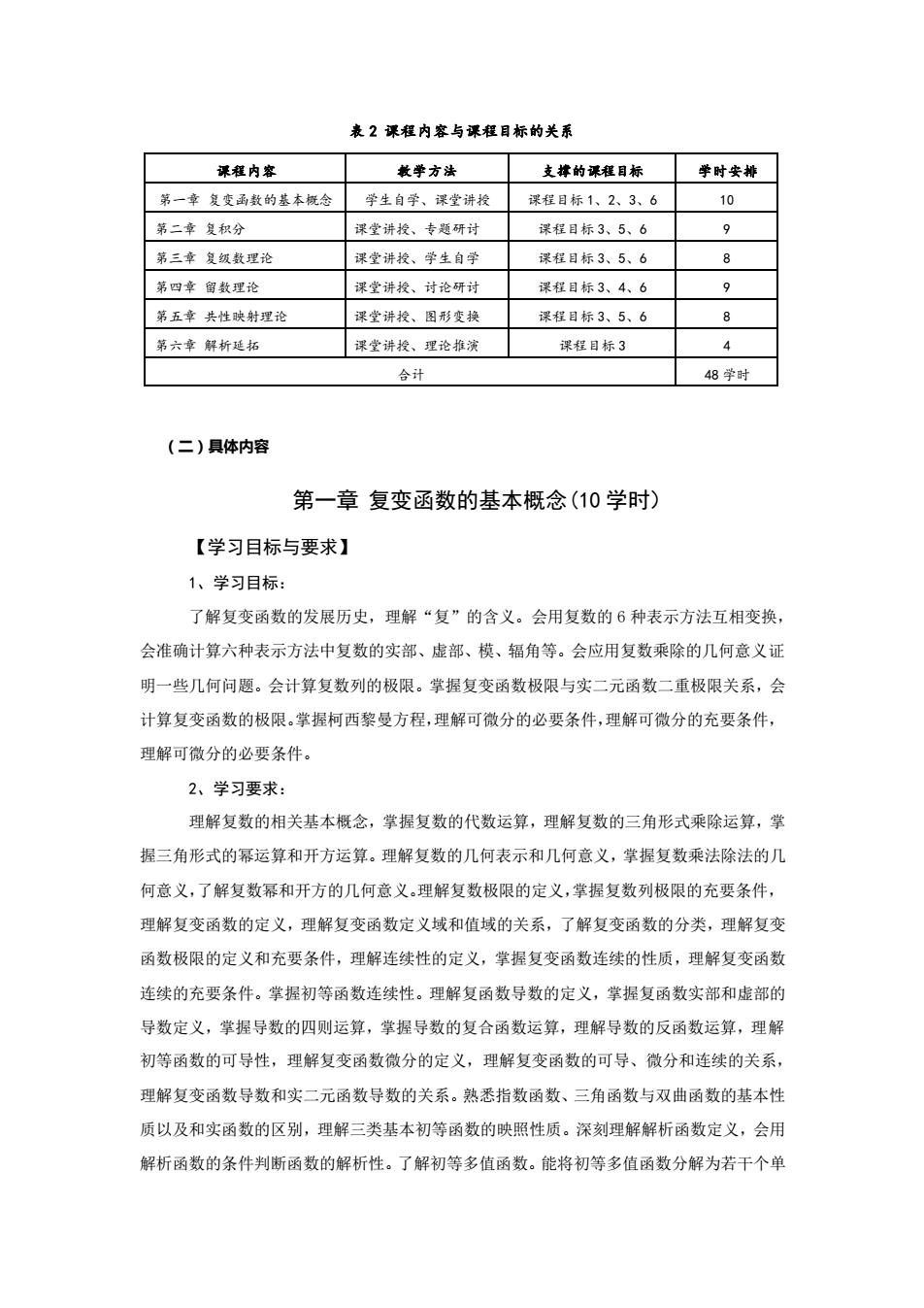
表2课程内容与课程目标的关系 评稚内容 教学方法 支撑的课程目标 学时安排 第一章复变函数的基本概念 学生自学、课堂讲授 课程目标1、2、3、6 10 第二章复积分 课堂讲授、专题研讨 课程目标3、5、6 。 第三章复级数理论 课堂讲授、学生自学 课程目标3、5、6 8 第四章留数理论 课堂讲授、讨论研讨 课程目标3、4、6 9 第五章共性映射理论 课堂讲授、图形变换 课程目标3、5、6 8 第六章解析延拓 课堂讲授、理论推演 课程目标3 4 合计 48学时 (二)具体内容 第一章复变函数的基本概念(10学时) 【学习目标与要求】 1、学习目标： 了解复变函数的发展历史，理解“复”的含义。会用复数的6种表示方法互相变换， 会准确计算六种表示方法中复数的实部、虚部、模、辐角等。会应用复数乘除的几何意义证 明一些几何问题。会计算复数列的极限。掌握复变函数极限与实二元函数二重极限关系，会 计算复变函数的极限。掌握柯西黎曼方程，理解可微分的必要条件，理解可微分的充要条件， 理解可微分的必要条件。 2、学习要求： 理解复数的相关基本概念，掌握复数的代数运算，理解复数的三角形式乘除运算，掌 握三角形式的幂运算和开方运算。理解复数的几何表示和几何意义，掌握复数乘法除法的几 何意义，了解复数幂和开方的几何意义。理解复数极限的定义，掌握复数列极限的充要条件， 理解复变函数的定义，理解复变函数定义域和值域的关系，了解复变函数的分类，理解复变 函数极限的定义和充要条件，理解连续性的定义，掌握复变函数连续的性质，理解复变函数 连续的充要条件。掌握初等函数连续性。理解复函数导数的定义，掌握复函数实部和虚部的 导数定义，掌握导数的四则运算，掌握导数的复合函数运算，理解导数的反函数运算，理解 初等函数的可导性，理解复变函数微分的定义，理解复变函数的可导、微分和连续的关系， 理解复变函数导数和实二元函数导数的关系。熟悉指数函数、三角函数与双曲函数的基本性 质以及和实函数的区别，理解三类基本初等函数的映照性质。深刻理解解析函数定义，会用 解析函数的条件判断函数的解析性。了解初等多值函数。能将初等多值函数分解为若干个单

表 2 课程内容与课程目标的关系 课程内容 教学方法 支撑的课程目标 学时安排 第一章 复变函数的基本概念 学生自学、课堂讲授 课程目标 1、2、3、6 10 第二章 复积分 课堂讲授、专题研讨 课程目标 3、5、6 9 第三章 复级数理论 课堂讲授、学生自学 课程目标 3、5、6 8 第四章 留数理论 课堂讲授、讨论研讨 课程目标 3、4、6 9 第五章 共性映射理论 课堂讲授、图形变换 课程目标 3、5、6 8 第六章 解析延拓 课堂讲授、理论推演 课程目标 3 4 合计 48 学时 （二）具体内容 第一章 复变函数的基本概念(10 学时） 【学习目标与要求】 1、学习目标： 了解复变函数的发展历史，理解“复”的含义。会用复数的 6 种表示方法互相变换， 会准确计算六种表示方法中复数的实部、虚部、模、辐角等。会应用复数乘除的几何意义证 明一些几何问题。会计算复数列的极限。掌握复变函数极限与实二元函数二重极限关系，会 计算复变函数的极限。掌握柯西黎曼方程，理解可微分的必要条件，理解可微分的充要条件， 理解可微分的必要条件。 2、学习要求： 理解复数的相关基本概念，掌握复数的代数运算，理解复数的三角形式乘除运算，掌 握三角形式的幂运算和开方运算。理解复数的几何表示和几何意义，掌握复数乘法除法的几 何意义，了解复数幂和开方的几何意义。理解复数极限的定义，掌握复数列极限的充要条件， 理解复变函数的定义，理解复变函数定义域和值域的关系，了解复变函数的分类，理解复变 函数极限的定义和充要条件，理解连续性的定义，掌握复变函数连续的性质，理解复变函数 连续的充要条件。掌握初等函数连续性。理解复函数导数的定义，掌握复函数实部和虚部的 导数定义，掌握导数的四则运算，掌握导数的复合函数运算，理解导数的反函数运算，理解 初等函数的可导性，理解复变函数微分的定义，理解复变函数的可导、微分和连续的关系， 理解复变函数导数和实二元函数导数的关系。熟悉指数函数、三角函数与双曲函数的基本性 质以及和实函数的区别，理解三类基本初等函数的映照性质。深刻理解解析函数定义，会用 解析函数的条件判断函数的解析性。了解初等多值函数。能将初等多值函数分解为若干个单

值函数。掌握对数函数的计算和反三角函数的计算。 【学习重点与难点】 1、学习重点：复变函数的发展历史，复数的6种表示方法，代数形式的四则运算， 三角形式的乘除运算和幂运算，开方运算。复数列极限的充要条件，复数列极限的计算，计 算复变函数的极限。复变函数连续的充要条件，初等函数连续性。复函数的微分，复函数可 微分的条件。初等解析函数，解析函数 2、学习难点：复数的坐标表示和向量表示的运算，复数几何意义，复数乘除幂和开 方的几何意义。复数列极限的定义，复变函数的分类，复变函数的极限，复变函数极限与实 二元函数二重极限关系，连续性的定义，复变函数连续的性质。复函数可微分的条件。初等 多值函数。 【学习内容】 1.1复数及其运算 1.2复变函数的极限与连续 1.3复变函数的导数与微分 1.4解析函数 第二章复积分(9学时) 【学习目标与要求】 1、学习目标： 灵活运用复函数积分的基本性质，理解复变函数的估值性质。熟练掌握柯西积分定理， 并能灵活应用，掌握柯西积分定理的推广形式，掌握不定积分和原函数的性质。会求拉普拉 斯方程的复变函数解法。了解复数边界积分方程的一般理论。会用解析函数实部和虚部表示 向量函数，会用解析函数表示静电场中的电场线和等势线。 2、学习要求： 理解并掌握复变函数积分的概念，掌握复变函数和实二元函数在曲线上积分的关系。 熟练掌握复变函数的积分计算并能灵活应用各种方法。灵活运用柯西积分公式，深刻理解解 析函数的无穷可微性，掌握柯西不等式与刘维尔定理，掌握代数学基本定理，掌握摩勒拉定 理。理解并掌握调和函数的定义和性质，了解调和函数的应用。理解并掌握拉普拉斯方程定 义，了解拉普拉斯方程的应用。理解并掌握复势的定义，熟悉平面向量场的解析函数表示法。 熟练掌握流体中各种场的解析函数表示。理解并掌握电场中的复势理论。 【学习重点与难点】 1、学习重点：复变函数积分的计算，复变函数积分的性质。柯西积分定理，柯西积

值函数。掌握对数函数的计算和反三角函数的计算。 【学习重点与难点】 1、学习重点：复变函数的发展历史，复数的 6 种表示方法，代数形式的四则运算， 三角形式的乘除运算和幂运算，开方运算。复数列极限的充要条件，复数列极限的计算，计 算复变函数的极限。复变函数连续的充要条件，初等函数连续性。复函数的微分，复函数可 微分的条件。初等解析函数，解析函数. 2、学习难点：复数的坐标表示和向量表示的运算，复数几何意义，复数乘除幂和开 方的几何意义。复数列极限的定义，复变函数的分类，复变函数的极限，复变函数极限与实 二元函数二重极限关系，连续性的定义，复变函数连续的性质。复函数可微分的条件。初等 多值函数。 【学习内容】 1.1 复数及其运算 1.2 复变函数的极限与连续 1.3 复变函数的导数与微分 1.4 解析函数 第二章 复积分(9 学时） 【学习目标与要求】 1、学习目标： 灵活运用复函数积分的基本性质，理解复变函数的估值性质。熟练掌握柯西积分定理， 并能灵活应用，掌握柯西积分定理的推广形式，掌握不定积分和原函数的性质。会求拉普拉 斯方程的复变函数解法。了解复数边界积分方程的一般理论。会用解析函数实部和虚部表示 向量函数，会用解析函数表示静电场中的电场线和等势线。 2、学习要求： 理解并掌握复变函数积分的概念，掌握复变函数和实二元函数在曲线上积分的关系。 熟练掌握复变函数的积分计算并能灵活应用各种方法。灵活运用柯西积分公式，深刻理解解 析函数的无穷可微性，掌握柯西不等式与刘维尔定理，掌握代数学基本定理，掌握摩勒拉定 理。理解并掌握调和函数的定义和性质，了解调和函数的应用。理解并掌握拉普拉斯方程定 义，了解拉普拉斯方程的应用。理解并掌握复势的定义，熟悉平面向量场的解析函数表示法。 熟练掌握流体中各种场的解析函数表示。理解并掌握电场中的复势理论。 【学习重点与难点】 1、学习重点：复变函数积分的计算，复变函数积分的性质。柯西积分定理，柯西积

分公式及其推论。调和函数的概念及其性质，调和函数与解析函数的关系。复变函数表示复 势。 2、学习难点：复变函数积分的概念。柯西积分定理的推广。柯西不等式与刘维尔定 理、代数学基本定理，摩勒拉定理。拉普拉斯方程的解答，复数边界积分方程。流体中的复 势应用，静电场中的复势应用。 【学习内容】 2.1复积分的定义 2.2柯西积分定理与柯西积分公式 2.3解析函数和调和函数关系 2.4复势理论及其应用 第三章复级数理论(8学时) 【学习目标与要求】 1、学习目标： 掌握复数项级数绝对收敛和条件收敛，掌握复数项级数收敛的性质，会计算复数项级 数的求和，掌握复函数项级数一致收敛的柯西收敛准准和优级数判别法，理解内闭一致收敛 定义。掌握解析函数的泰勒展式，会求初等函数的泰勒展式。明确解析函数零点的孤立性， 会判断解析函数零点的阶数，会证明解析函数恒为零的命题，会用反证法和最大模原理证明 复变函数命题。会求解析函数的洛朗展式。切实掌握孤立奇点的三种类型及其判断方法和性 质。会判断无穷远点孤立奇点类型。 2、学习要求： 理解复数项级数定义和复数项级数的收敛定义，理解复数项级数和实数项级数的关系。 理解复函数项级数定义，和函数定义，理解复函数项级数收敛和一致收敛的定义，掌握解析 函数可导性质。掌握幂级数的收敛半径求法及其性质，判断幂级数和函数的解析性。掌握解 析函数唯一性定理，会应用解析函数唯一性定理及其推论，了解解析函数局部和整体关系的 分析，理解最大模原理，会用最大模原理证明解析函数恒为常数，了解最大模原理与实函数 最大值的关系。理解洛朗展式和泰勒展式的关系。了解皮卡(Picard)定理。了解解析函数 在无穷远点的性质，了解整函数与亚纯函数的概念及其性质。 【学习重点与难点】 1、学习重点：解析函数项级数的导数性质。幂级数和的解析性判断。解析函数零点 的孤立性，解析函数唯一性定理。解析函数的洛朗展式。可去奇点、极点、本性奇点。解析 函数在无穷远点的性质

分公式及其推论。调和函数的概念及其性质，调和函数与解析函数的关系。复变函数表示复 势。 2、学习难点：复变函数积分的概念。柯西积分定理的推广。柯西不等式与刘维尔定 理、代数学基本定理，摩勒拉定理。拉普拉斯方程的解答，复数边界积分方程。流体中的复 势应用，静电场中的复势应用。 【学习内容】 2.1 复积分的定义 2.2 柯西积分定理与柯西积分公式 2.3 解析函数和调和函数关系 2.4 复势理论及其应用 第三章 复级数理论(8 学时） 【学习目标与要求】 1、学习目标： 掌握复数项级数绝对收敛和条件收敛，掌握复数项级数收敛的性质，会计算复数项级 数的求和，掌握复函数项级数一致收敛的柯西收敛准准和优级数判别法，理解内闭一致收敛 定义。掌握解析函数的泰勒展式，会求初等函数的泰勒展式。明确解析函数零点的孤立性， 会判断解析函数零点的阶数，会证明解析函数恒为零的命题，会用反证法和最大模原理证明 复变函数命题。会求解析函数的洛朗展式。切实掌握孤立奇点的三种类型及其判断方法和性 质。会判断无穷远点孤立奇点类型。 2、学习要求： 理解复数项级数定义和复数项级数的收敛定义，理解复数项级数和实数项级数的关系。 理解复函数项级数定义，和函数定义，理解复函数项级数收敛和一致收敛的定义，掌握解析 函数可导性质。掌握幂级数的收敛半径求法及其性质，判断幂级数和函数的解析性。掌握解 析函数唯一性定理，会应用解析函数唯一性定理及其推论，了解解析函数局部和整体关系的 分析，理解最大模原理，会用最大模原理证明解析函数恒为常数，了解最大模原理与实函数 最大值的关系。理解洛朗展式和泰勒展式的关系。了解皮卡（Picard）定理。了解解析函数 在无穷远点的性质，了解整函数与亚纯函数的概念及其性质。 【学习重点与难点】 1、学习重点：解析函数项级数的导数性质。幂级数和的解析性判断。解析函数零点 的孤立性，解析函数唯一性定理。解析函数的洛朗展式。可去奇点、极点、本性奇点。解析 函数在无穷远点的性质

2、学习难点：复函数项级数收敛和一致收敛的定义。幂级数的和函数在其收敛圆周 上的状况、一些初等函数的泰勒展式。最大模原理。洛朗级数与泰勒级数的关系。施瓦茨 (Schwarz)引理、皮卡(Picard)定理。整函数、亚纯函数。 【学习内容】 3.1复数项级数和复函数项级数 3.2幂级数 3.3解析函数的唯一性定理和零点孤立性（含最大模原理） 3.4洛朗级数 3.5孤立奇点 3.6整函数和亚纯函数 第四章孤立奇点留数的定义与计算(9学时) 【学习目标与要求】 1、学习目标： 掌握留数定理及其留数求法。会用用留数定理计算实积分，掌握儒歇定理。 2、学习要求： 掌握留数定理及其留数求法，理解无穷远点留数和有限点留数的关系，理解留数和复 变函数积分的关系。了解积分路径上有奇点的积分和应用多值函数的积分，理解辐角原理。 【学习重点与难点】 1、学习重点：留数的定义及留数定理、留数的求法。用留数定理计算实积分。 2、学习难点：留数的求法、无穷远点的留数。对数留数、辐角原理、儒歇定理。 【学习内容】 4.1留数及其计算 4.2留数计算实积分 4.3辐角原理 第五章共性映射(8学时) 【学习目标与要求】 1、学习目标： 掌握解析变换的特性，深刻理解导数的几何意义。会应用分式线性变换。掌握某些初 等函数所构成的共形映射

2、学习难点：复函数项级数收敛和一致收敛的定义。幂级数的和函数在其收敛圆周 上的状况、一些初等函数的泰勒展式。最大模原理。洛朗级数与泰勒级数的关系。施瓦茨 （Schwarz）引理、皮卡（Picard）定理。整函数、亚纯函数。 【学习内容】 3.1 复数项级数和复函数项级数 3.2 幂级数 3.3 解析函数的唯一性定理和零点孤立性(含最大模原理) 3.4 洛朗级数 3.5 孤立奇点 3.6 整函数和亚纯函数 第四章 孤立奇点留数的定义与计算(9 学时） 【学习目标与要求】 1、学习目标： 掌握留数定理及其留数求法。会用用留数定理计算实积分，掌握儒歇定理。 2、学习要求： 掌握留数定理及其留数求法，理解无穷远点留数和有限点留数的关系，理解留数和复 变函数积分的关系。了解积分路径上有奇点的积分和应用多值函数的积分，理解辐角原理。 【学习重点与难点】 1、学习重点：留数的定义及留数定理、留数的求法。用留数定理计算实积分。 2、学习难点：留数的求法、无穷远点的留数。对数留数、辐角原理、儒歇定理。 【学习内容】 4.1 留数及其计算 4.2 留数计算实积分 4.3 辐角原理 第五章 共性映射（8 学时） 【学习目标与要求】 1、学习目标： 掌握解析变换的特性，深刻理解导数的几何意义。会应用分式线性变换。掌握某些初 等函数所构成的共形映射

2、学习要求： 掌握解析变换的特性，深刻理解导数的几何意义，明确共形映射的概念。了解黎曼存 在定理和边界对应定理。掌握分式线性变换及其性质。深刻理解某些初等函数所构成的共形 映射。 【学习重点与难点】 1、学习重点：解析变换的保域性、解析变换的保角性-一导数的几何意义、单叶解析 变换的共形性。分式线性变换的共形性、分式线性变换的保交比性。幂函数与根式函数、指 数函数与对数函数。 2、学习难点：黎曼存在定理、边界对应定理。分式线性变换应用。由圆弧构成的两 角形区域的共形映射、儒可夫斯基函数的单叶性区域。 【学习内容】 5.1共形映射 5.2分式线性变换 5.3初等函数共形映射的综合应用 第六章解析延拓(4学时) 【学习目标与要求】 1、学习目标： 认识透弧解析延拓。 2、学习要求： 了解解析开拓的概念和一般原理。了解对称原理。了解完全解析函数及黎曼面的概念。 【学习重点与难点】 1、教学重点：解析延拓的幂级数方法。 2、教学难点：透弧直接解析延拓、黎曼-一施瓦茨对称原理。 【学习内容】 6.1解析延拓的概念与幂级数延拓 6.2透弧解析延拓、对称原理 6.3完全解析函数及黎曼面的概念 四、教学方法 1、授课：以课堂讲授为主，采取板书配以多媒体的方式。适当采取研讨案例方法。 2、习题课：进行典型问题分析，方法总结，难题讲解，与学生黑板演题相结合，训 练学生的逻辑思维能力，解题能力和思维严密性

2、学习要求： 掌握解析变换的特性，深刻理解导数的几何意义，明确共形映射的概念。了解黎曼存 在定理和边界对应定理。掌握分式线性变换及其性质。深刻理解某些初等函数所构成的共形 映射。 【学习重点与难点】 1、学习重点：解析变换的保域性、解析变换的保角性---导数的几何意义、单叶解析 变换的共形性。分式线性变换的共形性、分式线性变换的保交比性。幂函数与根式函数、指 数函数与对数函数。 2、学习难点：黎曼存在定理、边界对应定理。分式线性变换应用。由圆弧构成的两 角形区域的共形映射、儒可夫斯基函数的单叶性区域。 【学习内容】 5.1 共形映射 5.2 分式线性变换 5.3 初等函数共形映射的综合应用 第六章 解析延拓(4 学时） 【学习目标与要求】 1、学习目标： 认识透弧解析延拓。 2、学习要求： 了解解析开拓的概念和一般原理。了解对称原理。了解完全解析函数及黎曼面的概念。 【学习重点与难点】 1、教学重点：解析延拓的幂级数方法。 2、教学难点：透弧直接解析延拓、黎曼--施瓦茨对称原理。 【学习内容】 6.1 解析延拓的概念与幂级数延拓 6.2 透弧解析延拓、对称原理 6.3 完全解析函数及黎曼面的概念 四、教学方法 1、授课：以课堂讲授为主,采取板书配以多媒体的方式。适当采取研讨案例方法。 2、习题课：进行典型问题分析，方法总结，难题讲解，与学生黑板演题相结合，训 练学生的逻辑思维能力，解题能力和思维严密性

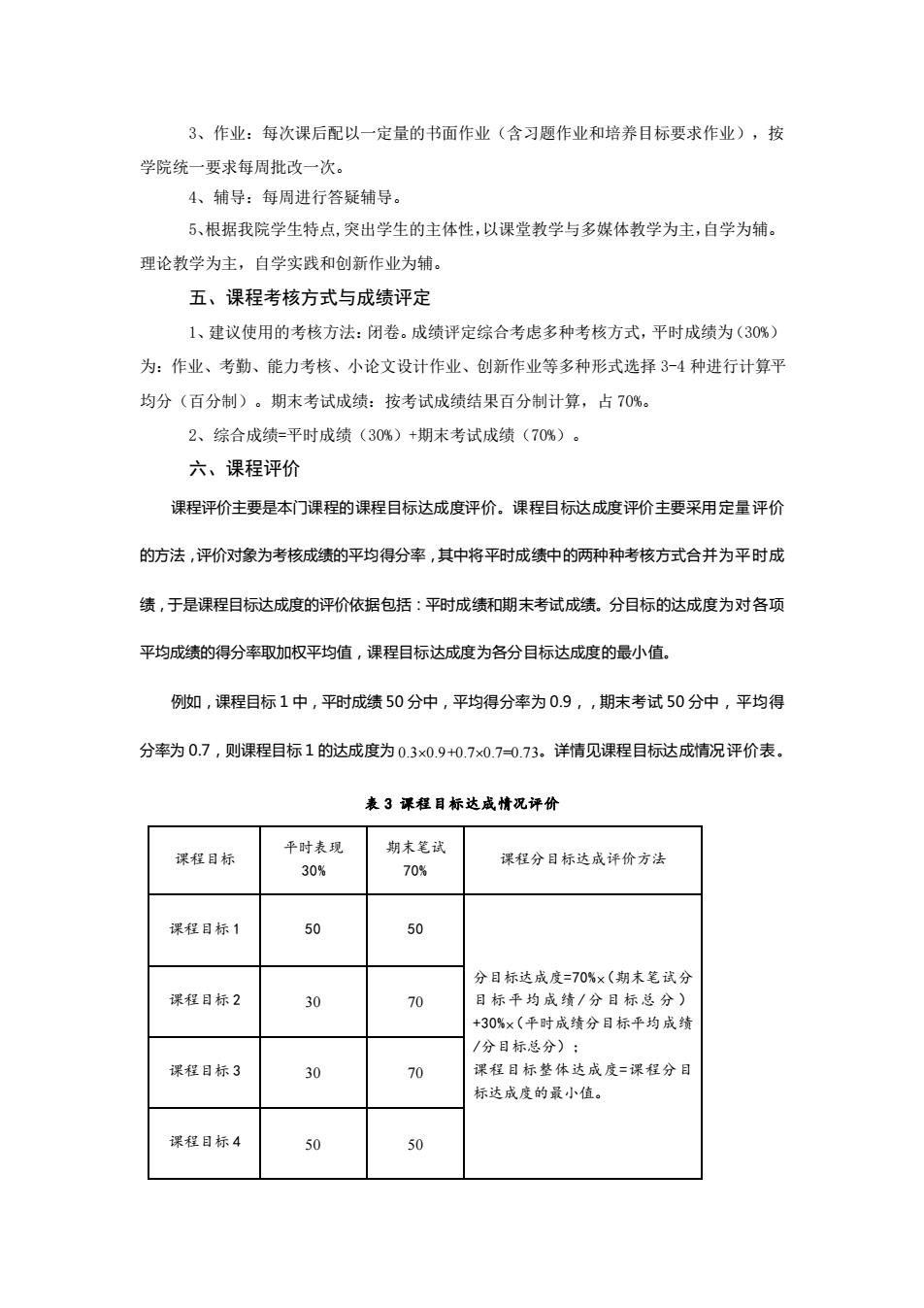
3、作业：每次课后配以一定量的书面作业（含习题作业和培养目标要求作业），按 学院统一要求每周批改一次。 4、辅导：每周进行答疑辅导。 5、根据我院学生特点，突出学生的主体性，以课堂教学与多媒体教学为主，自学为辅。 理论教学为主，自学实践和创新作业为辅。 五、课程考核方式与成绩评定 1、建议使用的考核方法：闭卷。成绩评定综合考虑多种考核方式，平时成绩为(30%) 为：作业、考勤、能力考核、小论文设计作业、创新作业等多种形式选择3-4种进行计算平 均分（百分制）。期末考试成绩：按考试成绩结果百分制计算，占70%。 2、综合成绩=平时成绩(30%)+期末考试成绩(70%)。 六、课程评价 课程评价主要是本门课程的课程目标达成度评价。课程目标达成度评价主要采用定量评价 的方法，评价对象为考核成绩的平均得分率，其中将平时成绩中的两种种考核方式合并为平时成 绩，于是课程目标达成度的评价依据包括：平时成绩和期未考试成绩。分目标的达成度为对各项 平均成绩的得分率取加权平均值，课程目标达成度为各分目标达成度的最小值。 例如，课程目标1中，平时成绩50分中，平均得分率为0.9，，期末考试50分中，平均得 分率为0.7，则课程目标1的达成度为0.3×0.9+0.7×0.7=0.73。详情见课程目标达成情况评价表。 表3课程目标达成情况评价 平时表现 期末笔试 课程目标 课程分目标达成评价方法 30% 70% 课程目标1 50 50 分目标达成度=70%×（期末笔试分 课程目标2 30 70 目标平均成绩/分目标总分) +30%×(平时成绩分目标平均成绩 /分目标总分)： 课程目标3 30 70 课程目标整体达成度=课程分目 标达成度的最小值。 课程目标4 50 50

3、作业：每次课后配以一定量的书面作业（含习题作业和培养目标要求作业），按 学院统一要求每周批改一次。 4、辅导：每周进行答疑辅导。 5、根据我院学生特点,突出学生的主体性，以课堂教学与多媒体教学为主，自学为辅。 理论教学为主，自学实践和创新作业为辅。 五、课程考核方式与成绩评定 1、建议使用的考核方法：闭卷。成绩评定综合考虑多种考核方式，平时成绩为（30%） 为：作业、考勤、能力考核、小论文设计作业、创新作业等多种形式选择 3-4 种进行计算平 均分（百分制）。期末考试成绩：按考试成绩结果百分制计算，占 70%。 2、综合成绩=平时成绩（30%）+期末考试成绩（70%）。 六、课程评价 课程评价主要是本门课程的课程目标达成度评价。课程目标达成度评价主要采用定量评价 的方法，评价对象为考核成绩的平均得分率，其中将平时成绩中的两种种考核方式合并为平时成 绩，于是课程目标达成度的评价依据包括：平时成绩和期末考试成绩。分目标的达成度为对各项 平均成绩的得分率取加权平均值，课程目标达成度为各分目标达成度的最小值。 例如，课程目标 1 中，平时成绩 50 分中，平均得分率为 0.9，，期末考试 50 分中，平均得 分率为 0.7，则课程目标 1 的达成度为 0.30.9+0.70.7=0.73。详情见课程目标达成情况评价表。 表 3 课程目标达成情况评价 课程目标 平时表现 30% 期末笔试 70% 课程分目标达成评价方法 课程目标 1 50 50 分目标达成度=70%（期末笔试分 目标平均成绩/ 分目标总 分 ） +30%（平时成绩分目标平均成绩 /分目标总分）； 课程目标整体达成度=课程分目 标达成度的最小值。 课程目标 2 30 70 课程目标 3 30 70 课程目标 4 50 50

课程目标5 40 60 课程目标6 50 50 七、教材与学习资源建议 (一)建议选用教材 建议使用教材：教学组的自编讲义 (二)主要参考书目 主要参考书： 1钟玉泉，复变函数论，北京：高等教育出版社，1997. 2余家荣，复变函数，北京：高等教育出版社，2014. 3华中科技大学数学系，复变函数和积分变换，北京：高等教育出版社，2008. 4苏变萍等，复变函数和积分变换，北京：高等教育出版社，2003. 5方企勤，复变函数，北京：北京大学出版社，2017. 6路见可，复变函数论，武汉：武汉大学出版社，2013. 7蔡贞东，万物皆复数，九州：九州出版社，2011 8陆庆乐，复变函数（第四版），北京：高等教育出版社，1996. 9王绵森，复变函数，北京：高等教育出版社，2008. 10沙巴特著，胥鸣伟，李振宇译，复分析导论，北京：高等教育出版社，2011. 11罗伯特格林，单复变函数论，北京：高等教育出版社，2017. 12拉夫连季耶夫，沙巴特，施祥林，夏定，复变函数论方法，北京：高等教育出版 社，2006. 13严镇军，复变函数，合肥：中国科学技术大学出版社，2001. 14路见可，钟寿国，刘士强，复变函数，武汉：武汉大学出版社，2007 15冯志新，沈永祥，复变函数，北京：北京大学出版社，2012. 16卢玉峰，刘西民，复变函数，北京：高等教育出版社，2016. 17杨贺菊，姚卫，复变函数，北京：清华大学出版社，2015. l8 JamesWardBrown,复变函数及应用，北京：机械工业出版社，2008. (三)其它课程资源 1、运城学院复变函数论共享资源培育课程

课程目标 5 40 60 课程目标 6 50 50 七、教材与学习资源建议 （一）建议选用教材 建议使用教材：教学组的自编讲义 （二）主要参考书目 主要参考书： 1 钟玉泉，复变函数论，北京：高等教育出版社，1997. 2 余家荣，复变函数，北京：高等教育出版社，2014. 3 华中科技大学数学系，复变函数和积分变换，北京：高等教育出版社，2008. 4 苏变萍等，复变函数和积分变换，北京：高等教育出版社，2003. 5 方企勤，复变函数，北京：北京大学出版社，2017. 6 路见可，复变函数论，武汉：武汉大学出版社，2013. 7 蔡贞东，万物皆复数，九州：九州出版社，2011. 8 陆庆乐，复变函数（第四版），北京：高等教育出版社，1996. 9 王绵森，复变函数，北京：高等教育出版社，2008. 10 沙巴特著，胥鸣伟，李振宇译，复分析导论，北京：高等教育出版社，2011. 11 罗伯特格林，单复变函数论，北京：高等教育出版社，2017. 12 拉夫连季耶夫，沙巴特，施祥林，夏定，复变函数论方法，北京：高等教育出版 社，2006. 13 严镇军，复变函数，合肥：中国科学技术大学出版社，2001. 14 路见可，钟寿国，刘士强，复变函数，武汉：武汉大学出版社，2007. 15 冯志新，沈永祥，复变函数，北京：北京大学出版社，2012. 16 卢玉峰，刘西民，复变函数，北京：高等教育出版社，2016. 17 杨贺菊，姚卫，复变函数，北京：清华大学出版社，2015. 18 JamesWardBrown，复变函数及应用，北京：机械工业出版社，2008. （三）其它课程资源 1、运城学院复变函数论共享资源培育课程

http://jpkc.ycu.edu.cn/fbhsl/ 2、华中科技大学复变函数与积分变换国家级精品课程 http://www.jingpinke.com/xpe/portal/22cf354b-1288-1000-887c- 5fd719521ae5?uuid=8a833999-2152448b-0121-52448c2e- 02d1&courseID=S0600777&resourceType=lessonplan 3、西安交通大学复变函数与积分变换壹课堂 http://www.1ketang.com/course/1440.html 八、其他需要说明的问题 根据师范认证下数学专业的培养目标及毕业要求，以及运城学院教学型、地方性和应 用型的特色，继承2019年的编制复变函数论教学大纲，同时参考其它高校复变函数论课程 的教学大纲，紧跟时代特点，突出师范类教育教学特点制定了此教学大纲。 制订：数学与信息技术学院 教研室：数学与应用数 学教研室 执笔人：刘俊俏 审订人：王琦 2021年5月

http://jpkc.ycu.edu.cn/fbhsl/ 2、华中科技大学复变函数与积分变换国家级精品课程 http://www.jingpinke.com/xpe/portal/22cf354b-1288-1000-887c- 5fd719521ae5?uuid=8a833999-2152448b-0121-52448c2e- 02d1&courseID=S0600777&resourceType=lessonplan 3、西安交通大学复变函数与积分变换壹课堂 http://www.1ketang.com/course/1440.html 八、其他需要说明的问题 根据师范认证下数学专业的培养目标及毕业要求，以及运城学院教学型、地方性和应 用型的特色，继承 2019 年的编制复变函数论教学大纲，同时参考其它高校复变函数论课程 的教学大纲，紧跟时代特点，突出师范类教育教学特点制定了此教学大纲。 制 订：数学与信息技术学院 教研室：数学与应用数 学教研室 执笔人：刘俊俏 审订人：王琦 2021 年 5 月