山东建筑大学：《高等数学》课程教学资源（PPT课件讲稿）第五章 定积分 第二节 微积分基本公式

第五章定积分 高等数学少学时 第二节微积分基本公式 一、变上限积分及其导数 二、牛顿一莱布尼茨公式 北京邮电大学出版社

1 第二节 微积分基本公式 一、变上限积分及其导数 二、牛顿 — 莱布尼茨公式

第五章 定积分 高等数学少学时 一、变上限积分及其导数 1.定义 设f(x)∈CLa,bl,x∈[a,b1,f(x)在区间[a,x] 定积分与积 上的上限变动的定积分f(x) :分变量无关 -S"f(odr 又确定了一个在[，b]上的新函数， y=f(t) 记作Φ(x),即 D(x)=∫if()dt(a≤x≤b) Φ(x) →f(x)的变上限积分函数 x b X 北京邮电大学出版社 2

2 ( ) ( )d ( ) x a x f t t a x b =     ( )d x a f x x  ( )d x a f t t  记作  ( x), 定积分与积 分变量无关 一、变上限积分及其导数 1. 定义 又确定了一个在 [ , ] a b 上的新函数， 即 设 f (x)C[a,b], x [a,b], f (x) a, x 上的上限变动的定积分 在区间 O a x b  ( ) x y = f (t) X Y f x( )的变上限积分函数

第五章 定积分 高等数学少学时 2.定理1若f(x)∈C[a,b]→D'(x)彐， 且 d=f)(asx) 证明思路：根据导数的定义，“求增量、算比值、取极限” 证x∈(a,b),使得x+△x∈(a,b), J y=f(x) AD=D(x+△x)-ΦD(x) =∫+af()d-∫if()dt L x5x+△xbx =∫ife)d+∫f()d-∫ife0a =∫*f0tFf传)Ax5e(c,x+a) 由积分中值定理 北京邮电大学出版社 3

3 x + x 使得x + x(a,b), 2. 定理1 且 ( ) d ( ) ( )d ( ) d x a x f t t f x a x b x  = =     Δ   = + − (x x x Δ ) ( ) 证  ( x) x  (a,b)， a x y = f (x) x y O b Δ  若 f (x)Ca,b   ( ) , x 证明思路：根据导数的定义，“求增量、算比值、取极限” ( )d d ( ) x x x a a f t t f t t +  = −   ( )d d ( ) x x x a x f t t f t t +  = +   ( )d x a − f t t  ( )d x x x f t t +  =  = f ( )x 由积分中值定理  (x, x + x)

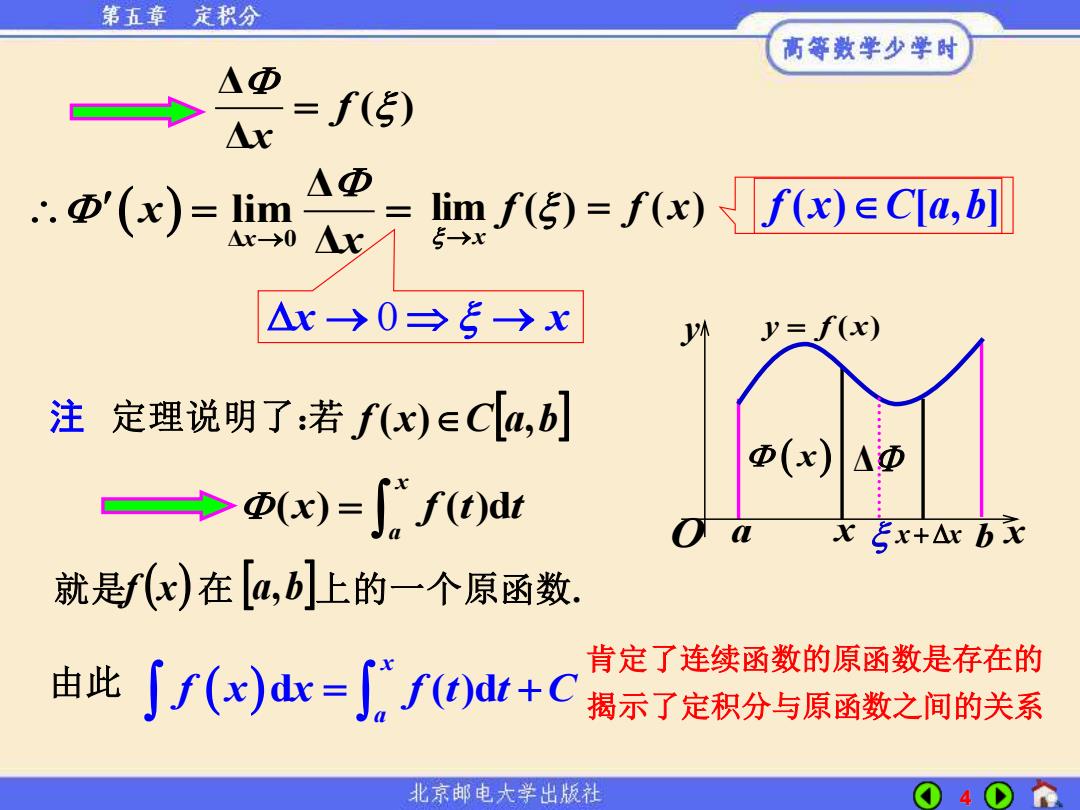
第五章 定积分 高等数学少学时 △Φ =f(5) x Φ ∴.Φ'(x)=im Ar limf()=f(x)f(x)ECla,b] Ar->0 5→x △x>0→5→x y=f(x) 注定理说明了：若fx)∈C[a,b] Φ(x) ΔΦ =>Φ(x)=∫ft)dr x5x+△xbx 就是f(x)在4，b]上的一个原函数， Jf(x)dx=S"f()dt+c 肯定了连续函数的原函数是存在的 由此 揭示了定积分与原函数之间的关系 北京邮电大学出版社

4 lim ( )  f →x ( ) Δ 0 Δ lim x Δ x x   →  = =  x + x  ( x) a x y = f (x) x y O b Δ  注 定理说明了：若 f (x)Ca,b ( ) ( )d x a x f t t =   就是 f (x) 在 a,b 上的一个原函数. 由此 ( )d ( )d x a f x x f t t C = +   肯定了连续函数的原函数是存在的 揭示了定积分与原函数之间的关系  →  → x x 0  = f ( x) f x C a b ( ) [ , ]  Δ ( ) Δ f x  = 

第五章 定积分 高等数学少学时 推广若f(x)∈CLa(x),Bx)小， a(x),B(x)在(a,b)内可导 &(2fou-ncxs( (1) &(nfew）=-f1axla (2) )-A-nacic (3) 北京邮电大学出版社 5

5     推广 若f (x)C[(x),(x)], (x),(x)在（a,b）内可导 ( ) d ( ) ( )d [ ( )] ( ) (1) d x a f t t f x x x =      ( ( ) ) d ( )d [ ( )] ( ) (2) d a x f t t f x x x  = −    ( ) ( ) ( ) d ( )d [ ( )] ( ) [ ( )] ( ) (3) d x x f t t f x x f x x x = −         

第五章 定积分 高等数学少学时 例1求 sin dt 解由定理1可知，上限为变量x的定积分其导数就是 被积函数，即 dsin'rdsin 例2求 sintdr 解 sindinyxin 北京邮电大学出版社 6

6 2 2 = sin ( ) x x  求 2 0 d sin d d x t t x 例  2 2 0 d sin d d x t t x       解  2 = 2 sin x x 2 2 0 d sin d sin d x t t x x   =      2 0 d sin d d x t t x        例１ 求 解 由定理１可知，上限为变量x的定积分其导数就是 被积函数，即

第五章 定积分 高等数学少学时 练习 ind &广s=sn6 s nx2dx=-sina2 cost2dt 例3求lim: x→0 X 0 解 odr） lim cosdt lim x)0 x x→0 (x)' lim cosx2 x→0 1 limcosx2 =1 x→0 北京邮电大学出版社 07

7 ( ) 2 0 0 cos d lim ( ) x x t t → x    2 0 cos limx 1 x → = 2 0 limcos x x → = 解 求 2 0 0 cos d lim x x t t → x  例 3 2 0 0 cos d lim x x t t → x =  00 = 1 练习 d 2 sin d d ba x x x  d 2 sin d d ba x x b  d 2 sin d d ba x x a  2 = sin b 2 = − sin a = 0

第五章 定积分 高等数学少学时 二、牛顿-一莱布尼茨公式 定理 2 f(x)ECla,b,F(x)=f(x) ∫f(x)d=F(o)-F(a 证·Fx是f)的一个原函数， 而D(x)=∫f)d地是f)的一个原函数， ∴.F(x)-Φ(x)=C(M≤x≤b) ∴.F(a)-Φ(a)=C=F(b)-D(b) 北京邮电大学出版社 8

8 ( )d ( ) ( ) b a f x x F b F a = −  证 F(x) 是 f (x) 的一个原函数，  − =   F x x C a x b ( )  ( ) ( )  − = F a a C ( )  ( ) f (x)Ca,b, F(x) = f (x) 二、牛顿--莱布尼茨公式 定理2 ( ) ( )d x a x f t t = 而   也是 f (x) 的一个原函数， = − F b b ( )  ( )

第五章 定积分 高等数学少学时 ∴F(b)-F(a)=(b)-(a) =∫f()dt-∫f()d =∫f()d .∫f()d=F(b)-F(a) 证毕 注公式又可记为：f()t=[F(x胎=Fb)-F(a) 牛顿莱布尼茨公式也称为微积分基本公式. 北京邮电大学出版社

9 f (t)dt F(x) F(b) F(a) b a b a = = −  牛顿-莱布尼茨公式也称为微积分基本公式. 注 公式又可记为：  − = − F b F a b a ( ) ( )   ( ) ( ) ( )d ( ) ( ) b a  = − f x x F b F a  证毕 ( )d d ( ) b a a a = − f t t f t t   ( )d b a = f t t 

第五章 定积分 高等数学少学时 例4求∫0x2x 解a[6- 1 -3 3 解 =a业：=n1-h2=-n2 北京邮电大学出版社 010C

10 12 dxx − −   12 ln −− = x 解 1 2 0 x xd  10 3 31   = x . 31 30 313 3 = − = 解 1 2 0 x xd 例 求  4 求 12 dxx − − 例 5 = ln 1 − ln 2 = − ln 2