
第四章不定积分 高等数学少学时 第四章不定积分 第一节 不定积分的概念与性质 第二节 换元积分法 第三节 分部积分法 第四节 有理函数的不定积分 第五节 积分表的使用 北京邮电大学出版社
1 第四章 不 定 积 分 第一节 不定积分的概念与性质 第二节 换元积分法 第三节 分部积分法 第四节 有理函数的不定积分 第五节 积分表的使用

第四章不定积分 高等数学少学时 第一节不定积分的棍念与性质 一、原函数与不定积分的概念 二、基本积分表 三、不定积分的基本性质 北京邮电大学出版社 2
2 第一节 不定积分的概念与性质 一、原函数与不定积分的概念 二、基本积分表 三、不定积分的基本性质

第四章不定积分 高等数学少学时 一、原函数与不定积分的概念 1.原函数的定义 (1)定义若在区间上,F(x)=f(x),或dF(x)=f(x), 则F(x)就称为(x)(或f(x))在I上的原函数 例如.(Sinx)'=c0s, .simx为cosx的原函数 显然,sinx+1,sinx+2,sinx+C等都是cosx的原函数。 北京邮电大学出版社 3
3 1. 原函数的定义 例如 (sin x) = cos x, sin x为cos x的原函数. ⑴ 定义 一、原函数与不定积分的概念 若在区间I上,F(x) = f (x), 或dF(x) = f (x)dx, 则F(x)就称为f (x) (或f (x)dx) 在I上的原函数. 显然, sin x +1, sin x + 2, sin x +C等都是cos x的原函数

第四章不定积分 高等数学少学时 (2)两个问题 ①原函数存在定理 如果函数f(x)在区间亚上连续则在☒间1上存在可导 函数F(x),使对任x∈I,都有F(x)=f(x) 即:连续函数一定有原函数 ②结论(原函数族问题) 设F(x为f(x)的原函数,则F(x)+C为f(x)的所有原函数 ()[F(x)+C]'=f(x) )设Φ(x)为fr(x)的另一个原函数则[(x)-F(x)】'=0 ∴.Φ(x)-F(x)=C Φ(x)=F(x)+C 北京邮电大学出版社
4 ⑵ 两个问题 ① 原函数存在定理 即:连续函数一定有原函数. 如果函数f (x)在区间I上连续,则在区间I上存在可导 函数F(x), 使对任一x I,都有F(x) = f (x). 设F(x)为f (x)的原函数,则F(x)+C为f (x)的所有原函数. ( ) F(x) C = f (x) i + ( ) ( ) = 0 则 x − F x (x)− F(x) = C (ii) 设(x)为f (x)的另一个原函数, ② 结论(原函数族问题) (x) = F(x) + C

第四章不定积分 高等数学少学时 2.不定积分的定义 定义在区间亚上,f(x的所有原函数称为(x)在区间 上的不定积分记为∫(x)dk ∫积分号, f(x)--被积函数, f(x)k--被积表达式,x-积分变量 设F(x为f(x)的一个原函数,于是 ∫fx)k=F(x)+C 北京邮电大学出版社 5
5 2. 不定积分的定义 定义 f (x)dx = F(x) + C 于是 在区间I上,f (x)的所有原函数称为f (x)在区间 记为 f x dx ( ) 上的 I ----积分变量 ----积分号, f (x)----被积函数, f (x)dx ----被积表达式, x 设F(x)为f (x)的一个原函数, 不定积分

第四章不定积分 高等数学少学时 例1求∫x2c. 解y=2- 3 +C. 取求. 解当x>,血对-∫=nx+C 当x<0,m(-r=(←= 0 ∫lk=ln(-x)tc. 总之 ∫k在=mr+C,x≠0 北京邮电大学出版社 6
6 例 1 2 x dx . 求 解 3 2 . 3x = + x dx C 例 2 1 dx . x 求 解 ( ) x x 1 ln = dx x C x = + ln 1 3 2 ) 31 ( x = x 当 x 0 , 当 x 0 , x x x 1 ( 1 ) 1 [ln( ) ] − = − − = 1 dx x C ln( ) . x = − + 总之 ln , 0 1 = + dx x C x x
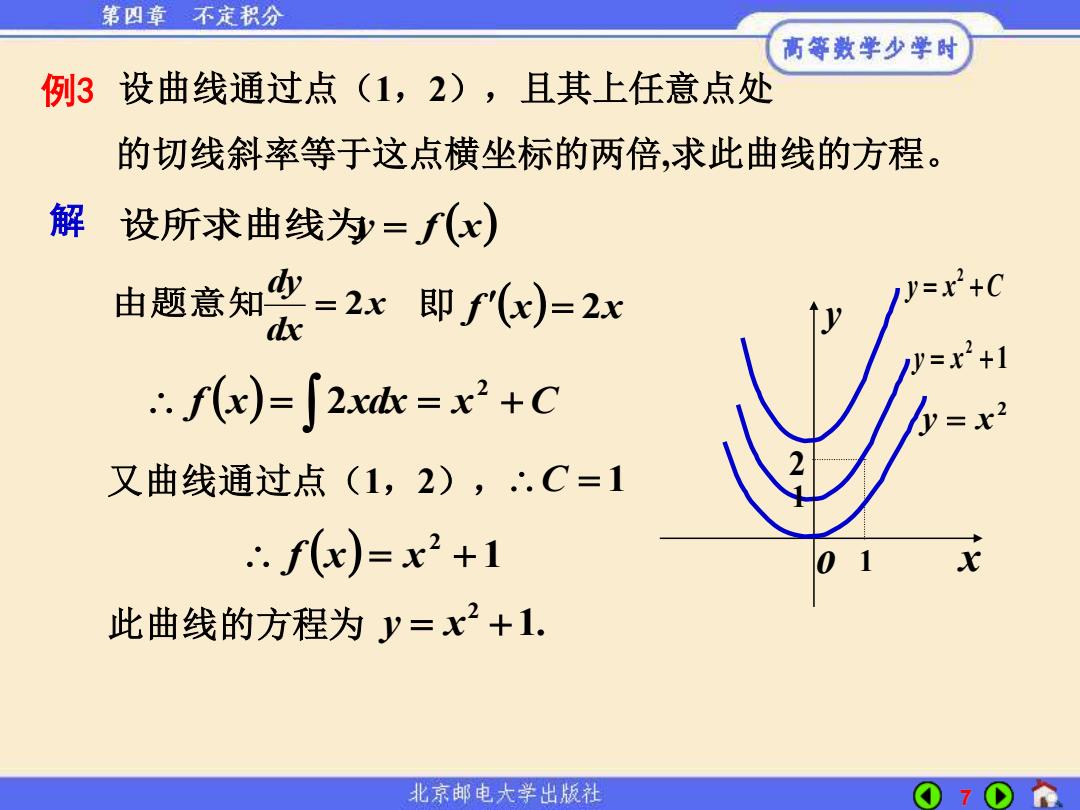
第四章不定积分 高等数学少学时 例3设曲线通过点(1,2),且其上任意点处 的切线斜率等于这点横坐标的两倍,求此曲线的方程。 解 设所求曲线为=f(x) 由题底知会=2x即1=2x y=x+C y=x2+1 f(x)=∫2xdc=x2+C y=x2 又曲线通过点(1,2),∴.C=1 ∴.f(x)=x2+1 此曲线的方程为y=2+1. 北京邮电大学出版社 7
7 f (x) = xdx = x + C 2 2 解 设所求曲线为y = f (x) x dx dy 由题意知 = 2 即 f (x) = 2x 又曲线通过点(1,2), C = 1 ( ) 1 2 f x = x + 此曲线的方程为 2 y x = +1. 例3 设曲线通过点(1,2),且其上任意点处 的切线斜率等于这点横坐标的两倍,求此曲线的方程。 1 2 y = x + 1 2 x y o 2 y = x 2 y x C = + 1

第四章不定积分 例4质点以初速y铅直上抛,不计阻力, 高等数学少学时 求它的运动规律。 解设初始时刻=0,x(0)=x,求x=x() x d2x dv dt2 dt =a(t)=-g x=x(t) )=∫←g)t=-gt+C xo=x(0) 由v(0)=yo,得C1=yo,∴.v(t)=-gt+yo x0=小0t=-g+,t=2+wt+C, 由x(0)=x,得C2=xo “0=-28+w+,1e0,刀] T为质点落地时刻. 北京邮电大学出版社 8
8 例4 0 质点以初速 v 铅直上抛,不计阻力, 解 0, (0) , ( ) 0 设初始时刻t = x = x 求x = x t v(t), dt dx = a t g dt dv dt d x = = ( ) = − 2 2 = − = − + 1 v(t) ( g)dt gt C (0) , , 0 1 0 由v = v 得C = v 0 v(t) = −gt + v (0) x0 = x x = x(t) x O 0 2 0 由x(0) = x , 得C = x 0 2 2 0 2 1 x(t) = v(t)dt = (−gt + v )dt = − gt + v t + C x t gt v t x t 0, T 2 1 ( ) 0 0 2 = − + + T为质点落地时刻. 求它的运动规律

第四章不定积分 高等数学少学时 注从不定积分定义,易知 &ff)或a=不 ∫F'(x)=F()+C或∫dF(x)=F(x)+C 由此,可以看出,积分与微分互为逆运算.上述关系可表述为: “先积后微,形式不变;先微后积,差个常数。” 北京邮电大学出版社 9
9 从不定积分定义,易知 或 d f (x)dx= f (x)dx 或 dF(x) = F(x) + C 注 由此,可以看出,积分与微分互为逆运算. 上述关系可表述为: “先积后微,形式不变;先微后积,差个常数

第四章不定积分 高等数学少学时 二、基本积分表 (1)kdx kx+C (8)[secixdx=tanx+C 可jra+c-9j-C 3&=m+C (10)Ssecxtanxdx=sec.x+C +文本=ainx+C (11)Scscxcotxde=-cscx+C (I2Sedk=e+C 3a杰-位+C 1n0 ()⑥sinxde=-cosx+C (14)shixdx=clx+C (7)fcosxd=sinx+C (15)clixdx=shx+C 北京邮电大学出版社 10
10 kx +C (2) x dx = 1 (3) dx x = 2 1 (4) 1 dx x = + 2 1 (5) 1 dx x = − (6) sin xdx = (7) cos xdx = 2 (8) sec tan xdx x C = + 2 (9) csc cot xdx x C = − + (10) sec tan sec x xdx x C = + (11) csc cot csc x xdx x C = − + (12) x x e dx e C = + (13) ln x x a a dx C a = + (1) kdx = ( ) x C + + − + 1 1 1 ln x + C arcsin x +C − cos x +C sin x +C arctan x +C 二、基本积分表 (14) shxdx chx C = + (15) chxdx shx C = +