
第一章 函数与极限 高等数学少学时 第三节备数的极限 一、 自变量趋于无穷大时函数的极限 二、自变量趋向于有限值时函数的极限 三、函数极限的性质 北京邮电大学出版社
1 第三节 函数的极限 一、自变量趋于无穷大时函数的极限 三、 函数极限的性质 二、自变量趋向于有限值时函数的极限

第一章 函数与极限 高等数学少学时 一、自变量趋于无穷大时函数的极限 当x→oo时函数fx)的极限,与当n→oo时数列xn=f孔m的极 限类似,所不同的是数列xm=f孔)的自变量只能取正整数,而函 数x)的自变量可以取任何实数.仿照数列极限的定义,函数的极 限定义如下: 定义1如果存在常数A,对于任意给定的正数ε(不论它多么小), 总存在正数X使得当x满足不等式xX时,对应的函数值fx)都 满足不等式 f(x)-A<6, 那么就称常数A为函数fx)当x→∞时的极限,记作 m=A或f)→A(6→o 北京邮电大学出版社
2 一、自变量趋于无穷大时函数的极限 当x→∞时函数f(x)的极限,与当n→∞时数列xn =f(n)的极 限类似,所不同的是数列xn =f(n)的自变量n只能取正整数,而函 数f(x)的自变量可以取任何实数.仿照数列极限的定义,函数的极 限定义如下: f (x) A x = → lim 或 f (x)→ A (x → ). 定义1 如果存在常数A,对于任意给定的正 总存在正数X,使得当x满足不等式|x|>X时,对应的函数值f(x)都 f (x)− A , 那么就称常数A为函数f (x)当x→∞时的极限,记作 数 (不论它多么小), 满足不等式
第一章 函数与极限 高等数学少学时 定义1可以简单的表述为: 寸ε>0,3X>0,当|x>X时,有f(x)-A0,X>0,当x>X,恒有f(x)A0,3X>0,当x0,使得当x>X, 函数y=f(心)的图形位于这两条直线间 4+8 A- -X 0 X X 北京邮电大学出版社 3
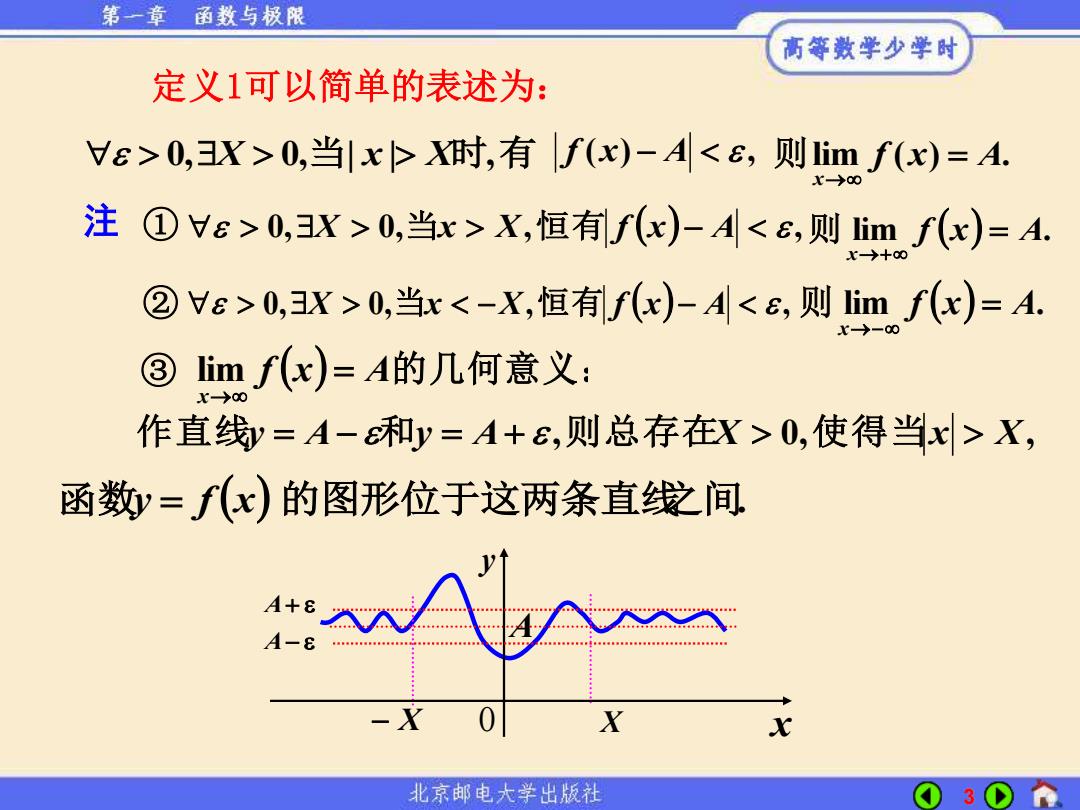
3 0,X 0,当| x | X时,有 f (x) − A , lim f (x) A. x = → 则 定义1可以简单的表述为: 0,X 0,当x X,恒 有 f (x) − A , lim f (x) A. x = →+ 则 lim f (x) A. x = →− 0,X 0,当x −X,恒 有 f (x) − A , 则 ① ② 注 f (x) A的几何意义: x = → lim 作直线y = A− 和y = A+ ,则总存在X 0,使得当x X, 函数y = f (x) 的图形位于这两条直线之间. − X 0 X x y A− A+ A ③
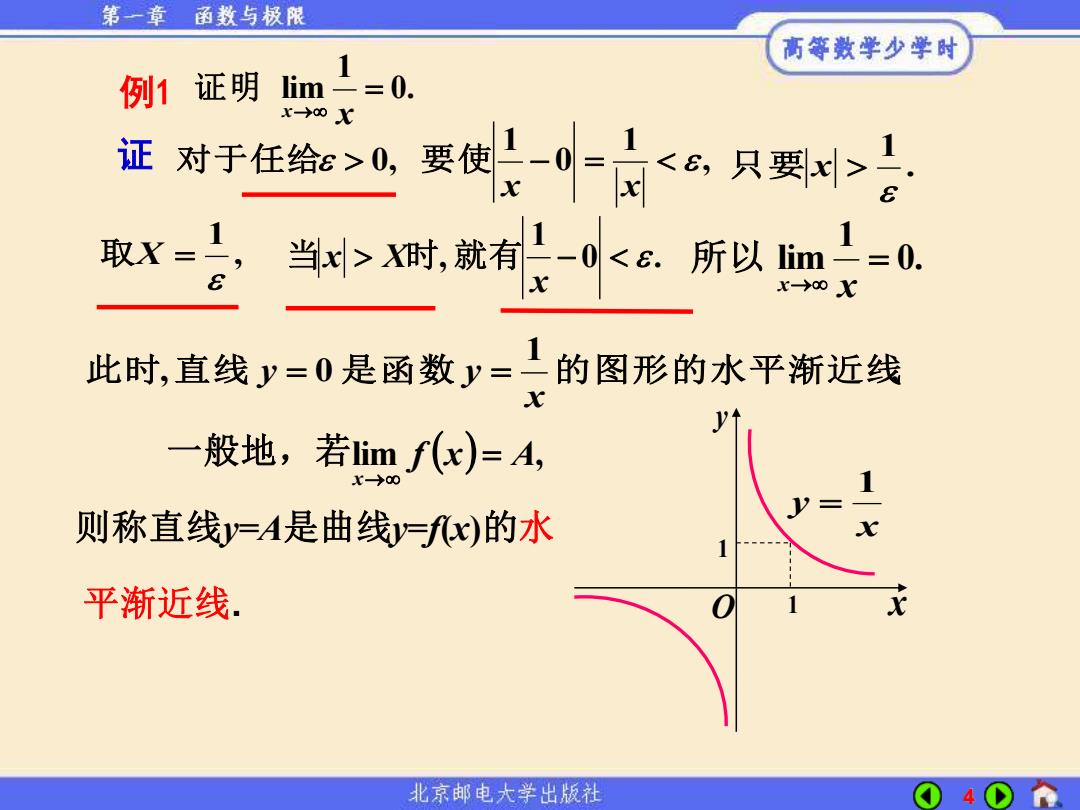
第一章 函数与极限 高等数学少学时 1 例1证明 im上=0. x->0o x 证对于任给:>0, 1 取X= 当>X时,就有上0<所以m0 x→oX 此时,直线y=0是函数y=1的图形的水平渐近线 C 一般地,若imf(x)=A, 1 则称直线y=A是曲线y=fx)的水 1 平渐近线. X 北京邮电大学出版社
4 , 1 0 1 0, − = x x 对于任给 要 使 , 1 取X = . 1 只要 x 0 . 1 , − x 当x X时 就有 0. 1 lim = x→ x 所以 . 1 此 时,直 线 0 是函数 的图形的水平渐近线 x y = y = 证 0. 1 lim = x→ x 例1 证明 一般地,若 lim f (x) A, x = → 则称直线y=A是曲线y=f(x)的水 平渐近线. x y 1 = O x y 1 1

第一章 函数与极限 高等数学少学时 二、自变量趋向于有限值时函数的极限 定义2如果存在常数A,对于任意给定的正数ε(不论它多么小), 总存在正数δ,使得当x满足不等式00,36>0,当0<x-xK6时,有f(x)-A<8,则 lim f(x)=A. x→xo 北京邮电大学出版社
5 f (x) A x x = → 0 lim ( ) ( ). 0 或 f x → A x → x 定义2 如果存在常数A,对于任意给定的正 总存在正数δ,使得当x满足不等式0<|x-x0 |< δ时,对应的函数值f(x) f (x)− A , 那么就称常数A为函数f (x)当x→ x0时的极限,记作 数 (不论它多么小), 二、自变量趋向于有限值时函数的极限 都满足不等式 0, 0,当0 | x − x0 | 时,有 f (x) − A ,则 lim ( ) . 0 f x A x x = → 定义2可以简单的表述为:

第一章 函数与极限 高等数学少学时 注①定义2中00,ヨ6>0,当x进入xo A 的δ去心邻域时,)的图形位于 A-8 x0-δX0x+8 X 直线y=A-&与y=A+8之间. 北京邮电大学出版社
6 注 f x A的几何解释: x x = → lim ( ) 0 0, 0, δ x x0 ε 当 进入 直线 y = A− ε与y = A+ ε ③ ① 定义2中0<|x-x0 |表示x无限接近x0时,函数f(x)的极限 是否存在,与f(x)在x=x0有没有定义无关. ② 满足0<|x-x0 |< δ的点x的集合称为x0的δ去心邻域;满足 满足|x-x0 |< δ的点x的集合称为x0的δ邻域. 的δ去心邻域时,f(x)的图形位于 之间. 。 x y = f (x) y A− A+ A 0 − x 0 x + 0 x

第一章 函数与极限 高等数学少学时 例2证明Iim(ac+b)=。+b,(a,b是常数,a≠0) 证 e>0,要使(+b)-(a+b)=ldx-x<, 只装k-X< 即可,取6=合则当<-小K5时,有 I(心+b)-(心+b)K8, 所以 四(ac+)=(ac,+b 注特别地①当a=0时,有limb=b. x→x0 ② 当a=1,b=0时,有imx=xo· x→x0 北京邮电大学出版社
7 lim ( ) , ( , , 0). 0 0 + = + → ax b ax b a b a x x 证明 是常数 0, ( ) ( ) , 0 0 ε 要使 ax + b − ax + b = a x − x ε 只 要 即可, | | 0 a x x − , a 取 = 则当0 x − x0 时,有 |( ) ( )| , 0 ax + b − ax + b ε lim ( ) ( ). 0 0 ax b ax b x x + = + → 注 证 例2 0 , lim . 0 a b b x x = = → ① 当 时 有 ② 1, 0 lim . 0 0 a b x x x x = = = → 当 时,有 特别地 所以

第一章 函数与极限 高等数学少学时 例3证明lim x2-9 =6. x→3 x-3 证f(x)在x=3处无定义不影响讨论数的极限 当3时, Eg-3=k-3 廿ε>0,取6=6,当0<x-3<时,有不等式 x2-9-6< x-3 成立.所以 x2-9 lim x→3 x-3 =6. 北京邮电大学出版社 8
8 f (x)在x = 3处无定义不影响讨论函数的极限. 6 3 6 3 9 2 − = + − − − x x x = x − 3 . 0,取 = ,当0 x − 3 时,有不等式 ( ) − − − 6 3 9 2 x x 6. 3 9 lim 2 3 = − − → x x x 6. 3 9 lim 2 3 = − − → x x x 证明 证 当x≠3时, 例3 成立.所以

第一章 函数与极限 高等数学少学时 左、右极限 ε>0,36>0,当x。-60,36>0,当x<x<x+6时,有 lf(x)-A<8, 成立,则称→x时,f(x)的右极限为4,记作 m)=A或fc)=A 北京邮电大学出版社 9
9 左、右极限 , ( ) , 成立,则称x → x0时 f x 的左极限为A 0, 0,当x0 − x x0时,有 f (x) − A , 0, 0,当x0 x x0 + 时,有 f (x) − A , f (x) A x x = → − 0 lim 记作 或 ( ) . f x0 = A − , ( ) , 成立,则称x → x0时 f x 的右极限为A f (x) A x x = → + 0 lim 记作 或 ( ) . f x0 = A +

第一章 函数与极限 高等数学少学时 定理1Iimf(c)=A的充要条件是imf(c)=Iimf(x)=A, x->x0 例4设)=,讨论当→0时断x)的极限是否存在 证f)=出_Lx0’0是分段函数的分界点.由于 lim f(x)=lim (-1)=-1, 0 x→0 四f)=im1=1 x0 f0)≠f0*) 所以当→0时,f(x)的极限不存在 北京邮电大学出版社 010C
10 lim ( ) lim ( ) lim ( ) . 0 0 0 f x A f x f x A x x x x x x = = = 定理1 → 的充要条件是 → + → − 证 lim ( ) lim ( 1) 1, 0 0 = − = − → − → − x x f x lim ( ) lim 1 1, 0 0 = = → + → + x x f x 例4 ( ) , x x 设 f x = 讨论当x →0时f (x)的极限是否存在. 所以当x →0时,f (x)的极限不存在. O x y (0 ) (0 ). − + f f , 1, 0 1, 0, ( ) − = = x x x x f x x=0是分段函数的分界点.由于