
第三章 线性方程组 目录 3.1 线性方程组和高斯 (Gauss)消元法 3.2n维向量组及向量组的线性组合 3.3向量组的线性相关性 3.4向量组的秩 3.5向量空间 3.6齐次线性方程组解的结构 3,7非齐次线性方程组解的结构 3.8应用举例 河套大学《线性代数》课件 第三章线性方程组 快东学司
第三章 线性方程组 □ 3.1 线性方程组和高斯(Gauss)消元法 □ 3.2 维向量组及向量组的线性组合 □ 3.3 向量组的线性相关性 □ 3.4 向量组的秩 □ 3.5 向量空间 □ 3.6 齐次线性方程组解的结构 □ 3.7 非齐次线性方程组解的结构 3.8 应用举例 目录 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 n

本节授裸计划 水人 (2课时) 尚本 必复习 新课3.8应用举例 第二十七次课 必小结 思考题及答案提示 必练习、作业及参考答案 河套大学《线性代数》课件 第三章线性方程组 快乐学司
快乐学习 以人 为本 ❖复习 ❖新课 3.8 应用举例 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 二 十 七 次 课 本节授课计划(2课时) 河套大学《线性代数》课件 第三章 线性方程组

水人 3.8 应用举例 尚本 主题调 1.线性方程组 2.应用 返回 河套大学《线性代数》课件 第三章线性方程组 快乐学司
快乐学习 以人 为本 主 题 词 3.8 应用举例 河套大学《线性代数》课件 第三章 线性方程组 1.线性方程组 2.应用 返回

相关内容回预 水人 尚本 数学建模;线性模型;线性方程组。 河套大学《线性代数》课件 第三章线性方程组 快乐学司
快乐学习 以人 相关内容回顾 为本 河套大学《线性代数》课件 第三章 线性方程组 数学建模;线性模型;线性方程组

水人 新课 3.8 应用举例 幸 本节中的数学模型都是线性的,即每个模型 都用线性方程组表示,通常写成向量或矩阵的形 式.由于自然现象通常都是线性的,或者当变量 取值在合理范围内时近似于线性,因此线性模型 的研究非常重要.此外,线性模型比复杂的非线 性模型更易于用计算机进行计算. 一次的 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
一次的 以人 新课 3.8 应用举例 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 本节中的数学模型都是线性的,即每个模型 都用线性方程组表示,通常写成向量或矩阵的形 式. 由于自然现象通常都是线性的,或者当变量 取值在合理范围内时近似于线性,因此线性模型 的研究非常重要. 此外,线性模型比复杂的非线 性模型更易于用计算机进行计算

水人 新课 3.8.1网络流模型1 幸 网络流模型广泛应用于交通、运输、通讯、 电力分配、城市规划、任务分派以及计算机辅助 设计等众多领域.当科学家、工程师和经济学家 研究某种网络中的流量问题时,线性方程组就自 然产生了, 河套大学《线性代数》课件 第三章线性方程组 快东学司
以人 新课 3.8.1 网络流模型 1 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 网络流模型广泛应用于交通、运输、通讯、 电力分配、城市规划、任务分派以及计算机辅助 设计等众多领域. 当科学家、工程师和经济学家 研究某种网络中的流量问题时,线性方程组就自 然产生了

0人 新课 3.8.1网络流模型2 幸 例如,城市规划设计人员和交通工程师监控 城市道路网络内的交通流量,电气工程师计算电 路中流经的电流,经济学家分析产品通过批发商 和零售商网络从生产者到消费者的分配等.大多 数网络流模型中的方程组都包含了数百甚至上千 个未知量和线性方程 河套大学《线性代数》课件 第三章线性方程组 快东学日
以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 3.8.1 网络流模型 2 例如,城市规划设计人员和交通工程师监控 城市道路网络内的交通流量,电气工程师计算电 路中流经的电流,经济学家分析产品通过批发商 和零售商网络从生产者到消费者的分配等. 大多 数网络流模型中的方程组都包含了数百甚至上千 个未知量和线性方程

水人 新课 3.8.1网络流模型3 幸 一个网络由一个点集以及连接部分或全部 点的直线或弧线构成.网络中的点称为联结点(或 节点),网络中的连接线称为分支.每一个分支中 的流量方向已经指定,并且流量(或流速)已知 或者已标为变量. 网络流的基本假设是网络中流入与流出的 总量相等,并且每个连结点流入与流出的总量也 相等. 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 3.8.1 网络流模型 3 一个网络由一个点集以及连接部分或全部 点的直线或弧线构成.网络中的点称为联结点(或 节点),网络中的连接线称为分支.每一个分支中 的流量方向已经指定,并且流量(或流速)已知 或者已标为变量. 网络流的基本假设是网络中流入与流出的 总量相等,并且每个连结点流入与流出的总量也 相等
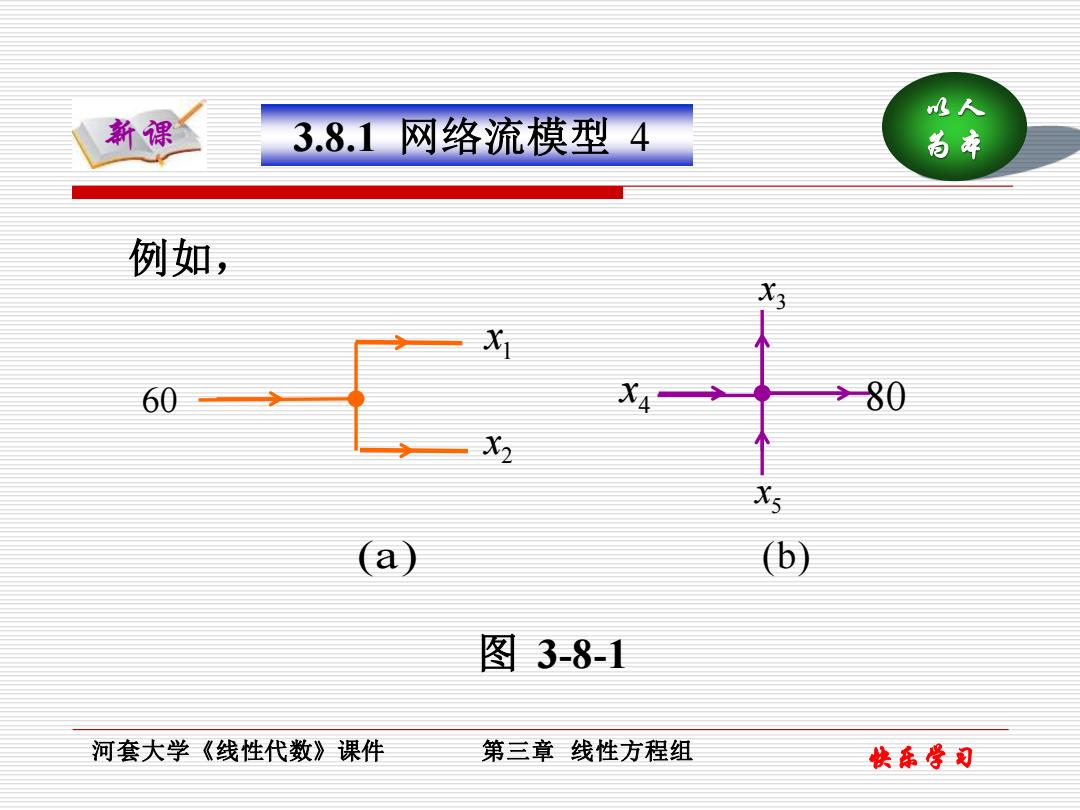
0人 新课 3.8.1网络流模型4 尚本 例如, X3 X 60 XA 80 一X2 (a) (b) 图3-81 河套大学《线性代数》课件 第三章线性方程组 快东学司
以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 80 1 x 2 x 3 x 4 x 5 x 60 (a) (b) 图 3-8-1 例如, 3.8.1 网络流模型 4

0人 新课 3.8.1网络流模型 5 幸 例如,图3-81分别说明了流量从一个或两个 分支流入连结点,x,x2,x分别表示从其它分支流 出的流量.x,x,表示从其它分支流入的流量, 因为流量在每个连结点守恒,所以有 x1+x2=60和x4+x,=x3+80 在类似的网络模式中,每个连结点的流量都 可以用一个线性方程组来表示 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 3.8.1 网络流模型 5 例如,图3-8-1分别说明了流量从一个或两个 4 5 x , x 80. x4 + x5 = x3 + 分支流入连结点, 出的流量. 因为流量在每个连结点守恒,所以有 x1 + x2 = 60 和 1 2 3 x , x , x 分别表示从其它分支流 表示从其它分支流入的流量. 在类似的网络模式中,每个连结点的流量都 可以用一个线性方程组来表示