
第四章 相似矩阵与与一次型 目录 4.1n维向量的内积 4,2矩阵的特征值与特征向量 4.3相以矩阵 4.4二次型 (2) 4.5正定二次型 四4.6应用举例 河套大学《线性代数》课件 第四章相似矩阵与二次型 快东学司
□ 4.1 维向量的内积 □ 4.2 矩阵的特征值与特征向量 □ 4.3 相似矩阵 □ 4.4 二次型(2) □ 4.5 正定二次型 4.6 应用举例 目录 快乐学习 n 河套大学《线性代数》课件 第四章 相似矩阵与二次型 第四章 相似矩阵与二次型

本节授裸计划 水人 (2课时) 尚本 必复习 必新课 第三十五次课 4.6应用举例 必小结 思考题及答案提示 练习、作业及参考答案 河套大学《线性代数》课件 第四章相似矩阵与二次型 快乐学司
快乐学习 以人 为本 ❖复习 ❖新课 4.6 应用举例 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 三 十 五 次 课 本节授课计划(2课时) 河套大学《线性代数》课件 第四章 相似矩阵与二次型

相吴内容回预 人人 尚本 1.矩阵的特征值与特征向量的概念? 设A是n阶方阵,若存在数λ和n维非 零向量5,使得 A5=入5 则称数入为矩阵A的特征值,称非零向量5 为矩阵A的属于特征值2的特征向量, 河套大学《线性代数》课件 第四章相似矩阵与二次型 快乐骨司
设 是 阶方阵,若存在数 和 维非 零向量 ,使得 则称数 为矩阵 的特征值,称非零向量 为矩阵 的属于特征值 的特征向量. 快乐学习 以人 相关内容回顾 为本 河套大学《线性代数》课件 第四章 相似矩阵与二次型 1.矩阵的特征值与特征向量的概念? A n n A = A A

水人 4.6应用举例 尚本 1.特征值 2.特征向量 3.对角化 4.应用 返回 河套大学《线性代数》课件 第四章相似矩阵与二次型 快东学司
快乐学习 以人 为本 主 题 词 4.6 应用举例 返回 河套大学《线性代数》课件 第四章 相似矩阵与二次型 1.特征值 2.特征向量 3.对角化 4.应用

水人 新课 4.6应用举例 幸 要理解并预测由线性差分方程x=Ax,所描 述的动态系统的长期行为或演化,关键在于掌握 矩阵的特征值与特征向量.在本节中,我们将通 过应用实例来介绍矩阵对角化在离散动态系统模 型中的应用,这些应用实例主要针对生态问题 是因为相对于物理问题或工程问题,它们更容易 说明和解释,但实际上动态系统在许多科学领域 中都会出现 河套大学《线性代数》课件 第四章相似矩阵与二次型 快乐骨司
以人 新课 为本 河套大学《线性代数》课件 第四章 相似矩阵与二次型 快乐学习 4.6 应用举例 1 要理解并预测由线性差分方程 所描 述的动态系统的长期行为或演化,关键在于掌握 矩阵 的特征值与特征向量.在本节中,我们将通 过应用实例来介绍矩阵对角化在离散动态系统模 型中的应用,这些应用实例主要针对生态问题, 是因为相对于物理问题或工程问题,它们更容易 说明和解释,但实际上动态系统在许多科学领域 中都会出现. A n 1 Axn x + =

0人 新课 4.6 应用举例2 幸 例4.6.1 ( 教师职业转换预测问题)在某城 市有15万人具有本科以上学历,其中有1.5万人 是教师,据调查,平均每年有10%的人从教师职 业转为其它职业,又有1%的人从其它职业转为教 师职业,试预测10年以后这15万人中还有多少人 在从事教师职业? 河套大学《线性代数》课件 第四章相似矩阵与二次型 快东学日
以人 新课 为本 河套大学《线性代数》课件 第四章 相似矩阵与二次型 快乐学习 4.6 应用举例 2 例4.6.1 (教师职业转换预测问题)在某城 市有15万人具有本科以上学历,其中有1.5万人 是教师,据调查,平均每年有10%的人从教师职 业转为其它职业,又有1%的人从其它职业转为教 师职业,试预测10年以后这15万人中还有多少人 在从事教师职业?

0人 新课 4.6 应用举例3 尚幸 解:用x,表示第n年后从事教师职业和其它 其它职业的人数,则x 1.5 用矩阵 13.5 0.90 0.01 A-(a) 0.100.99 表示教师职业和其它职业间的转移情况,其中 a=0.90,表示每年有90%的人原来是教师现在还 教师 河套大学《线性代数》课件 第四章相似矩阵与二次型 快乐骨司
解:用 表示第 年后从事教师职业和其它 以人 新课 为本 河套大学《线性代数》课件 第四章 相似矩阵与二次型 快乐学习 4.6 应用举例 3 n x n = 13.5 1.5 0 x = = 0.10 0.99 0.90 0.01 ( ) A aij a11= 0.90 其它职业的人数,则 , 用矩阵 表示教师职业和其它职业间的转移情况,其中 表示每年有90%的人原来是教师现在还 教师;

0人 新课 4.6应用举例4 尚幸 a21=0.0表示每年有10%的人从教师职业转为其它 职业 显然 0.900.01 71.5 1.485 X1=AXo= 0.100.9913.5 13.515 即一年后,从事教师职业和其它职业的人数分别为 1.485万及13.515万.又 河套大学《线性代数》课件 第四章相似矩阵与二次型 快乐骨司
以人 新课 为本 河套大学《线性代数》课件 第四章 相似矩阵与二次型 快乐学习 4.6 应用举例 4 职业. 显然 a21= 0.10 = = = 13.515 1.485 13.5 1.5 0.10 0.99 0.90 0.01 1 Ax0 x 表示每年有10%的人从教师职业转为其它 即一年后,从事教师职业和其它职业的人数分别为 1.485万及13.515万. 又

0人 新课 4.6 应用举例5 幸 x2=Ax A2Xo,,Xn=AX1=A"Xo, 所以xo-x,为计算A需要先将A对角化. 元-0.9 -0.01 AE-A= (2-0.9(2-0.99)-0.001 01λ-0.99 =2-1.891+0.891-0.001=22-1.89λ+0.890=0. 求得 1=1,入2=0.89 河套大学《线性代数》课件 第四章相似矩阵与二次型 快东骨司
所以 为计算 需要先将 对角化. 以人 新课 为本 河套大学《线性代数》课件 第四章 相似矩阵与二次型 快乐学习 4.6 应用举例 5 , , , 0 1 0 2 2 1 x Ax A x x Ax A x n = = n = n− = , 0 10 10 x = A x 10 A A ( 0.9)( 0.99) 0.001 0.1 0.99 0.9 0.01 = − − − − − − − − = E A 1.89 0.891 0.001 2 = − + − 1.89 0.890 0. 2 = − + = 求得 1, 1 = 0.89. 2 =
水人 新课 4.6 应用举例 6 幸 将=1代入(.E-A)=0,得属于=1的特 征向量5, 将2=0.89代入(2E-A0=0,得属于12=0.89 特征向量5 故由定理4.3.2知A可对角化. P=(5,52)= ,有 河套大学《线性代数》课件 第四章相似矩阵与二次型 快东学司
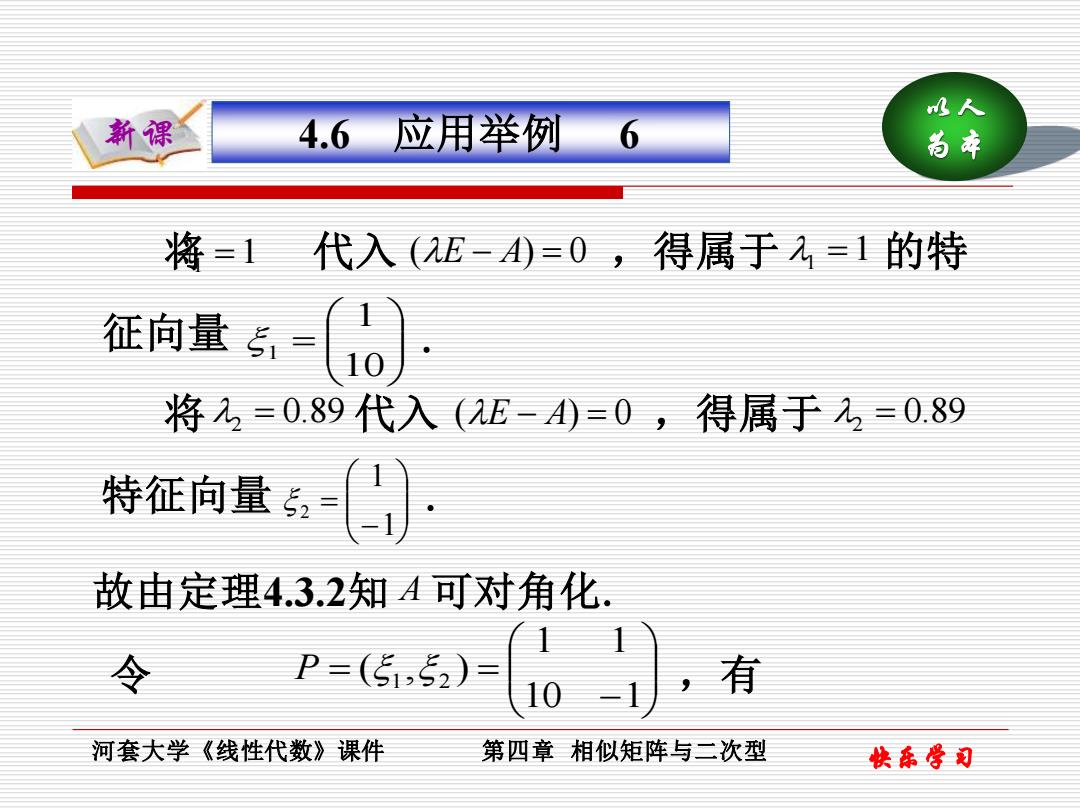
将 代入 ,得属于 的特 以人 新课 为本 河套大学《线性代数》课件 第四章 相似矩阵与二次型 快乐学习 4.6 应用举例 6 1 =1 (E − A) = 0 1 =1 = 10 1 1 2 = 0.89 2 = 0.89 − = 1 1 2 故由定理4.3.2知 A 可对角化. 令 − = = 10 1 1 1 ( , ) P 1 2 征向量 . 将 代入 (E − A) = 0 ,得属于 特征向量 . ,有