
第三章 线性方程组 目录 四 3.1线性方程组和高斯 (Gauss) 消元法 3.2维向量组及向量组的线性组合 3.3向量组的线性相关性 3.4向量组的秩 3.5向量空间 3.6齐火线性方程组解的结构 3.7非齐次线性方程组解的结构 3.8应用举例 河套大学《线性代数》课件 第三章线性方程组 快乐学司
第三章 线性方程组 3.1 线性方程组和高斯(Gauss)消元法 □ 3.2 维向量组及向量组的线性组合 □ 3.3 向量组的线性相关性 □ 3.4 向量组的秩 □ 3.5 向量空间 □ 3.6 齐次线性方程组解的结构 □ 3.7 非齐次线性方程组解的结构 □ 3.8 应用举例 目录 河套大学《线性代数》课件 第三章 线性方程组 快乐学习

本节授裸计划 水人 (2课时) 尚本 必复习 必新课 3.1线性方程组和高 (Gauss)消元法(2) 第十九驶课 3.1.3线性方程组的高斯(Gauss) 消元法 小结 必思考题及答案提示 练习、作业及参考答案 河套大学《线性代数》课件 第三章线性方程组 快乐学可
快乐学习 以人 为本 ❖复习 ❖新课 3.1 线性方程组和高(Gauss)消元法(2) 3.1.3 线性方程组的高斯(Gauss)消元法 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 十 九 次 课 本节授课计划(2课时) 河套大学《线性代数》课件 第三章 线性方程组

水人 3.1线性方程组和高斯(Gauss)消元法 尚本 主题调 1.消元法 2.阶梯形方程组 3.最简形矩阵 返回 河套大学《线性代数》课件 第三章线性方程组 快乐学司
快乐学习 以人 为本 主 题 词 3.1 线性方程组和高斯(Gauss)消元法 河套大学《线性代数》课件 第三章 线性方程组 1. 消元法 2. 阶梯形方程组 3. 最简形矩阵 返回

相关内容回预 水人 尚本 什么矩阵的阶梯形、最简形? 利用什么方法将矩阵化为阶梯形、最简形? 利用行初等变换法 什么叫矩阵的秩? 矩阵的非零子式的最高阶数或阶梯型矩阵非零 行的行数. 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
快乐学习 以人 相关内容回顾 为本 河套大学《线性代数》课件 第三章 线性方程组 什么矩阵的阶梯形、最简形? 利用什么方法将矩阵化为阶梯形、最简形? 什么叫矩阵的秩? 矩阵的非零子式的最高阶数或阶梯型矩阵非零 行的行数. 利用行初等变换法

水人 新课 3.1.3线性方程组的Gauss消元法1 尚本 引例言 用消元法解线性方程组 2x1+2x2-x3=6, x12x2+4x3=3 5x1+7x2+x3=28 解为观察消元过程,我们将消元过程中的每一 个步骤的方程组及其对应的矩阵一并列出; 2x+2x2-X3=6, 2 2 x12x2+4x3=3, 对应 -2 43 1 5x+7x2+x3=28 57 28 河套大学《线性代数》课件 第三章线性方程组 快东骨司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法1 + + = − + = + − = 5 7 28. 2 4 3, 2 2 6, 1 2 3 1 2 3 1 2 3 x x x x x x x x x 引例 用消元法解线性方程组 个步骤的方程组及其对应的矩阵一并列出; 解 为观察消元过程,我们将消元过程中的每一 + + = − + = + − = 5 7 28. 2 4 3, 2 2 6, 1 2 3 1 2 3 1 2 3 x x x x x x x x x 对应 ⎯→ − − 5 7 1 28 1 2 4 3 2 2 1 6 ① ①
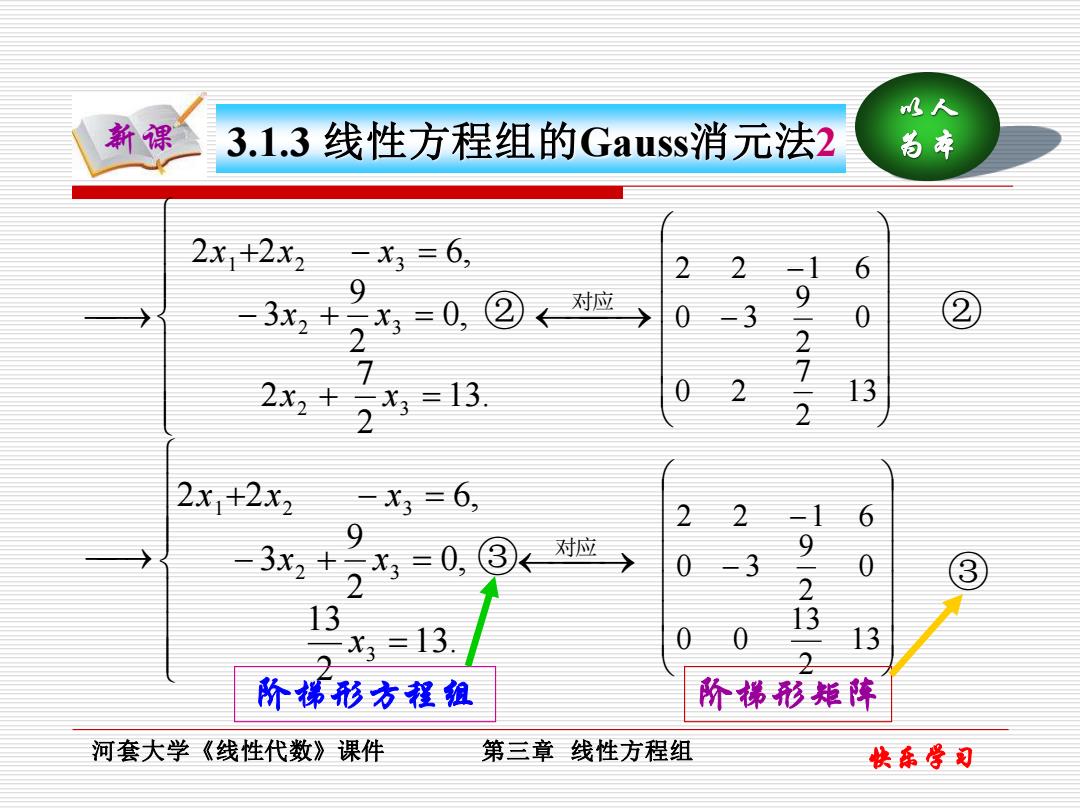
水人 新课 3.1.3线性方程组的Gauss消元法2 尚本 2x1+2x2-x3=6, 2 2 6 对应 9 3x2+x3=0, 0 -3 0 2 27 2x2+ 213 2 13 2 2x1+2x2 -=X3=6, 2 2 6 9 3+=0® 对应 9 0 -3 0 2 13 3=13 0 13 阶梯形方程组 阶梯形矩阵 河套大学《线性代数》课件 第三章线性方程组 快东学司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法2 + = − + = + − = 13. 2 7 2 0, 2 9 3 2 2 6, 2 3 2 3 1 2 3 x x x x x x x 对应 ⎯→ − − 13 2 7 0 2 0 2 9 0 3 2 2 1 6 = − + = + − = 13. 2 13 0, 2 9 3 2 2 6, 3 2 3 1 2 3 x x x x x x 对应 ⎯→ ② ② ③ − − 13 2 13 0 0 0 2 9 0 3 2 2 1 6 ③ ⎯→ ⎯→ 阶梯形方程组 阶梯形矩阵

水人 新课 3.1.3线性方程组的Gauss消元法3 尚本 2x1+2x2-X3=6, 2 2 6 9 3x,+2=0 4 对应 0 -3 4 X3=2 2x1+2x2 =8, 220 8 ⑤ 对应 -3x2 =-9 0 -30 ¥3=2 阶梯形方程组 阶梯形矩阵 河套大学《线性代数》课件 第三章线性方程组 快东学司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法3 ⎯→ = − + = + − = 2. 0, 2 9 3 2 2 6, 3 2 3 1 2 3 x x x x x x 对应 ⎯→ − − 0 0 1 2 0 2 9 0 3 2 2 1 6 ④ ④ ⎯→ = − = − + = 2. 3 9, 2 2 8, 3 2 1 2 x x x x 对应 ⎯→ − − 0 0 1 2 0 3 0 9 2 2 0 8 ⑤ ⑤ 阶梯形方程组 阶梯形矩阵

水人 新课 3.1.3线性方程组的Gauss消元法4 尚本 2x1+2X2 =8, 2 2 8 X2 =3, ⑥ 对应 ¥3=2 2X1 =2, 对应 X2 =3, X3=2 阶梯形大程组 阶梯形矩阵 河套大学《线性代数》课件 第三章线性方程组 快东学司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法4 ⎯→ = = + = 2. 3, 2 2 8, 3 2 1 2 x x x x 对应 ⎯→ 0 0 1 2 0 1 0 3 2 2 0 8 ⎯→ = = = 2. 3, 2 2, 3 2 1 x x x 对应 ⎯→ 0 0 1 2 0 1 0 3 2 0 0 2 ⑥ ⑥ ⑦ ⑦ 阶梯形方程组 阶梯形矩阵
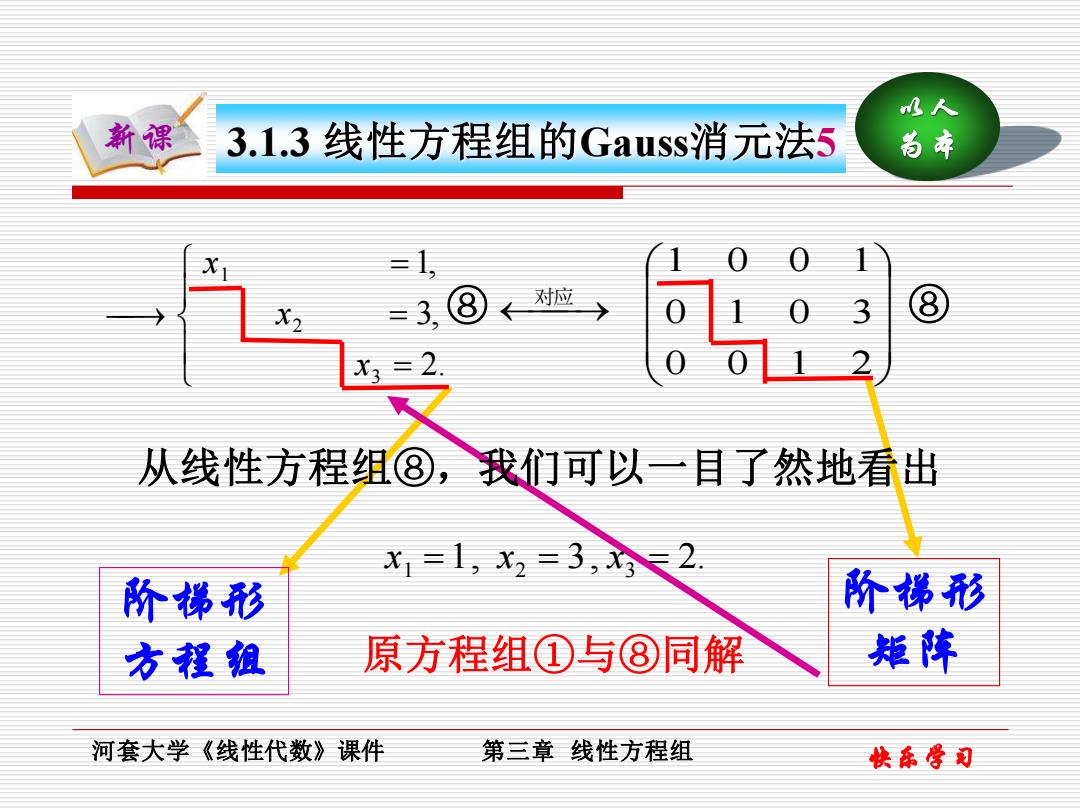
水人 新课 3.1.3线性方程组的Gauss:消元法5 尚本 =3, 对应 X2 8 =2 从线性方程组⑧,我们可以一耳了然地看出 x1=1,x2=3,3≤2 阶梯形 阶梯形 方程组 原方程组①与⑧同解 矩阵 河套大学《线性代数》课件 第三章线性方程组 快乐学司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法5 ⎯→ = = = 2. 3, 1, 3 2 1 x x x 对应 ⎯→ 0 0 1 2 0 1 0 3 1 0 0 1 1, 3, 2. x1 = x2 = x3 = ⑧ 从线性方程组⑧,我们可以一目了然地看出 ⑧ 阶梯形 方程组 阶梯形 原方程组①与⑧同解 矩阵

水人 新课 3.1.3线性方程组的Gauss:消元法6 尚本 在第二章我们给出线性方程组的初等变换的概 念,引出了矩阵的初等变换的概念在第二章还给 出了阶梯形矩阵的概念,当然也对应有阶梯形方 程组的概念.从上述引例可以看出:消元法的目的 就是利用方程组的初等变换将原方程组化为阶梯 形方程组,显然这个梯形方程组与原线性方程 组同解,解这个阶梯形方程组得到原方程组的解 如果用矩阵表示其系数和常数项,则将原方程组 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法6 在第二章我们给出线性方程组的初等变换的概 念,引出了矩阵的初等变换的概念.在第二章还给 出了阶梯形矩阵的概念,当然也对应有阶梯形方 程组的概念.从上述引例可以看出:消元法的目的 就是利用方程组的初等变换将原方程组化为阶梯 形方程组,显然这个阶梯形方程组与原线性方程 组同解,解这个阶梯形方程组得到原方程组的解. 如果用矩阵表示其系数和常数项,则将原方程组