
第一章函数与极限 高等数学少学时 第四节无穷小量与无穷大量 一、无穷小量 二、无穷大量 北京邮电大学出版社 01
1 第四节 无穷小量与无穷大量 一、无穷小量 二、无穷大量

第一章函数与极限 高等数学少学时 一、无穷小量 1.无穷小的定义 定义1如果imf(x)=0(或Iimf(x)=0),那么称函数) x→X0 为当x→x(或x→∞)时的无穷小量,简称为无穷小. 例如::lim(x-1)=0,∴f(x)=x-1是当r→1时的无穷小 im1=0,函数是当x→o时的无穷小 x→0C C 注①讲无穷小必须指明自变量的变化趋向. ②无穷小与很小的数不能等同,无穷小是变量.零是可作 为无穷小的唯一常数. 北京邮电大学出版社 2
2 一、无穷小量 1.无穷小的定义 定义1 lim ( ) 0 lim ( ) 0 , 0 如果 = (或 = ) → → f x f x x x x 那么称函数f(x) 为当x→x0 (或x→∞)时的无穷小量,简称为无穷小. lim( 1) 0, 1 − = → x x 0, 1 lim = x→ x 例如: f (x) = x −1是当x →1时的无穷小. . 1 函数 是当x → 时的无穷小 x 注 ① 讲无穷小必须指明自变量的变化趋向. ② 无穷小与很小的数不能等同,无穷小是变量.零是可作 为无穷小的唯一常数

第一章 函数与极限 高等数学少学时 无穷小与函数极限有下述关系: 定理1imf(x)=A台f(x)=A+a,其中ima(x)=0. x→x0 x→x0 (x→0) (x→o) 证先证必要性 由已知Iimf(x)=A,现设a=f(x)-A.根据极限的定义, x→X0 对于ε>0,36>0,使得当0<x-x<6时,有 f(x)-A=a<s, 即 lim a(x)=0. x→x0 北京邮电大学出版社
3 无穷小与函数极限有下述关系: ( ) = → → f x A x x x ( ) 0 定理1 lim f (x) = A+ , lim ( ) 0 . ( ) 0 = → → x x x x 其中 证 对于 0 , 0 ,使得当0 x − x0 时,有 现设 = f (x)− A. 先证必要性 由已知 f x A, x x = → lim ( ) 0 根据极限的定义, f (x)− A = , lim ( ) 0 . 0 = → x x x 即

第一章 函数与极限 高等数学少学时 再证充分性 设f(x)=A+a,其中A是常数,是无穷小x→x)由无穷小 的定义,对于ε>0,6>0,使得当0<x-x<6,有 a=f(x)-A<s, 即 imf(x)=4. 类似地可证明→x,x→,x→o时的情形 北京邮电大学出版社
4 ( ) , , ( ). x A A x x0 设f = + 其中 是常数 是无穷小 → 0, 0 ,使得当0 x − x0 ,有 lim ( ) . 0 f x A x x = → , , . 类似地可证明x → x0 − x → x0 + x → 时的情形 再证充分性 由无穷小 的定义,对于 = f (x)− A , 即

第一章函数与极限 高等数学少学时 2.无穷小性质 定理2在某一极限过程中,有限个无穷小的和仍为无穷小. 证只对两个无穷小的情形加以证明. 设a,均为当→x时的无穷小y=a+B.由无穷小的定义, >0,对于>0,36>0,d,>0,使得当0<x-<d时,有 a<;当0<x-x<d时,有1BK取6=min{6,6b则当 0<x-x<时,有 y≤|a+|B< c. 2 所以a+为x→x时的无穷小 北京邮电大学出版社 5
5 2.无穷小性质 定理2 在某一极限过程中,有限个无穷小的和仍为无穷小. 证 只对两个无穷小的情形加以证明. , , . 设α β均为当x → x0时的无穷小 = + δ1 0,δ2 0,使得当0 x − x0 δ1时,有 ; 2 0 , 当 x − x0 δ2 时 . 2 | | 有 β 取 = min 1 , 2 ,则当 . 2 2 + + = . 所以α + β为x → x0时的无穷小 0 , 2 0, ε 对于 由无穷小的定义, 0 x − x0 时,有

第一章 函数与极限 高等数学少学时 定理3在某一极限过程中,无穷小与有界函数的乘积仍为 无穷小. 证设a(x)是当r→x时的无穷小u(x)在x的某去心邻 域内有界即归M>0和6>0,当00,就£>0而言,6,>0,使得当0<x-x<6,时,有 M a(xy<取5=ninf⊙,,当0<x-<时,有 l)ati) 所以(x)a是当r→x,时的无穷小 定理2,3对于x→x,x→x,x→o时的情形类似可以证明 北京邮电大学出版社 6
6 证 定理3 在某一极限过程中,无穷小与有界函数的乘积仍为 无穷小. min{ , }, 取δ = δ1 δ 2 0, 0 , 0, δ2 M 对 ε 就 而言 ( ) . 设 x 是当x → x0时的无穷小 0 , ( ) . 域内有界,即M 0和 1 0, 当 x − x0 δ1时 有 u x M 使得当0 x − x0 δ2时,有 当0 x − x0 δ时,有 ( ) . 所以u x 是当x → x0时的无穷小 ( ) ( ) | ( )|| ( )| , = = M u x α x u x α x M u(x)在 x0 的某去心邻 ( ) . M ε α x 2,3 , , . 定 理 对 于x → x0 − x → x0 + x → 时的情形类似可以证明

第一章 函数与极限 高等数学少学时 推论1在某一极限过程中,常数与无穷小的乘积仍为无穷小. 推论2在某一极限过程中,有限多个无穷小的乘积仍为无穷小. 1 例1求极限lim xcos x→0 X 解因为0时, sin ≤1,而1imx=0,所以lim xsin2=0. x0 x→0 例2求极限im sinx X→0 解 因为sinxs1,lim=0,所以im sin x 0. x-→0X x→∞C 常见错误 im。_全a这im=0 SHX 001 北京邮电大学出版社 7
7 推论1 在某一极限过程中,常数与无穷小的乘积仍为无穷小. 推论2 在某一极限过程中,有限多个无穷小的乘积仍为无穷小. lim 0, 0 = → x x 而 0. 1 lim sin 0 = → x x x 1, 所以 1 sin x 解 . 1 lim cos 0 x x x→ 例1 求极限 因为x≠0时, . sin lim x x x→ 求极限 因为|sin x | 1, 0, 1 lim = x→ x 0. sin lim = → x x x 所以 例2 解 0 1 lim sin lim sin lim = = → → → x x x x x x x 常见错误

第一章 函数与极限 高等数学少学时 二、无穷大量 定义2如果对于任意给定的正数M心0(不论它多么大),总 存在>0(或正数),当0X)时,有f(x)>M, f(x)>Mfx)<-M则称f(x当x→x(或x→o)时为无穷大量 为正无穷大量,为负无穷大量,简称无穷大.记作 f)=ol或mf()=∞} lim f(x)=+oo lim f(x)=-co x→X0 X→x0 (x→0) (x→0) 北京邮电大学出版社 8
8 二、无穷大量 当0 x − x0 δ ( ) ( ) , 则称f x 当x → x0 或x → 时为无穷大量 定义2 f (x) M f (x) −M (或 x X)时, 有 f (x) M, 如果对于任意给定的正数M>0(不论它多么大),总 存在δ>0(或正数X), 为正无穷大量,为负无穷大量,简称无穷大.记作 lim ( ) ( lim ( ) ). 0 = = → → f x f x x x x 或 = + → → lim ( ) ( ) 0 f x x x x = − → → lim ( ) ( ) 0 f x x x x
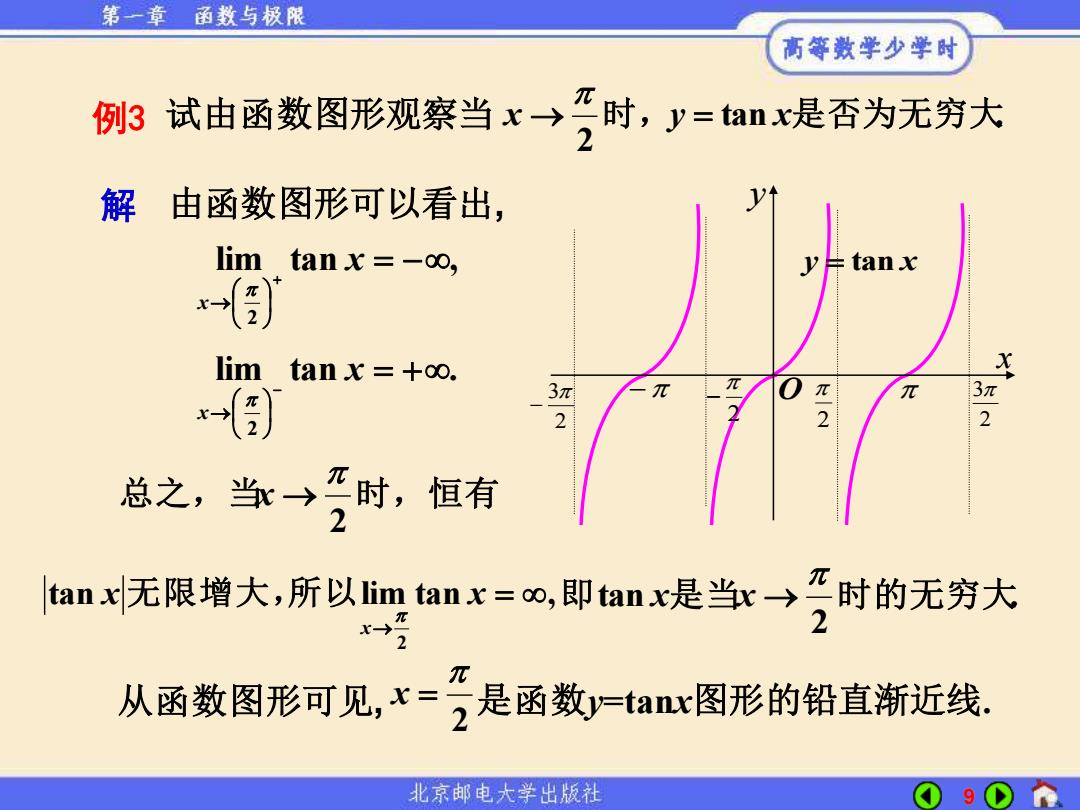
第一章 函数与极限 高等数学少学时 例3试由函数图形观察当x→ 时,y=anx是否为无穷大 解由函数图形可以看出, lim tanx=-o0, lim tanx=+00. 3π 3π 2 2 总之,当→匹时,恒有 tanx无限增大,所以lim tanx=o,即tanx是当r→元时的无穷大 2 2 2 从函数图形可见,x=2是函数tan图形的铅直渐新近线. 北京邮电大学出版社 9
9 例3 试由函数图形观察当 tan . 2 x → 时,y = x是否为无穷大 x O 2 2 3 2 − − 2 3 − y y = tan x 解 由函数图形可以看出, lim tan , 2 = − + → x x lim tan . 2 = + − → x x 总之,当 时,恒有 2 x → tan x 无限增大, lim tan , 2 = → x x 所以 . 2 即tan 是当 时的无穷大 x x → 从函数图形可见, 2 x = 是函数y=tanx图形的铅直渐近线

第一章 函数与极限 高等数学少学时 一般地,如果Iimf(x)=oo,则直线=x是y=f(x)的图形 形的铅直渐近线. 无穷小与无穷大的关系 定理4在某一极限过程中,fx)为无穷大,则 为无 穷小;反之,如果fx)是无穷小,且fx)0,则 和为无穷大 证设imf(x)=oo.任给>0,对于M=1>0, 36>0,当 0M-即有 <, 由无穷小的定义, 何是当→x时的无穷小 北京邮电大学出版社 10
10 一般地 如果 f (x) 则直线x x 是y f (x)的图形 x x = = = → 0 , lim , 0 形的铅直渐近线. 无穷小与无穷大的关系 ( ) . 1 为无穷大 f x 定理4 在某一极限过程中,f(x)为无穷大,则 ( ) 为无 1 f x 穷小;反之,如果f(x)是无穷小,且f(x) ≠0,则 lim ( ) . 0 = → f x x x 设 ( ) , 1 f x M = ( ) , 1 ε f x 即有 ( ) . 1 是 当x x0时的无穷小 f x → 任给ε 0, 0, 1 = ε 证 对于M δ 0,当 0 x − x0 δ时, 有 由无穷小的定义