
第六章微分方程 高等数学少学时 第六章微分方程 第一节 微分方程的基本概念 第二节 一阶微分方程及其解法 第三节 可降阶的高阶微分方程 第四节 二阶常系数线性微分方程 第六章 习题课 北京邮电大学出版社
1 第六章 微分方程 第一节 微分方程的基本概念 第二节 一阶微分方程及其解法 第三节 可降阶的高阶微分方程 第四节 二阶常系数线性微分方程 第六章 习题课

第六章微分方程 高等数学少学时 第一节微分方程的基本棍念 一、引例 二、微分方程的基本概念 北京邮电大学出版社 O20
2 第一节 微分方程的基本概念 二、微分方程的基本概念 一、引例

第六章微分方程 高等数学少学时 一、引例 例1一曲线通过点(1,3),且在该曲线上任一点Pcy)处的 切线的斜率为4x3,求这曲线的方程 解设曲线方程为y=y(x),根据导数的几何意义,有 =y'(x)=4x (6-1) dx 两边积分,得 y=∫4xd即y=r+C 6-2) 其中C是任意常数.把=1,y=3代入(6-2)式,得C=2 于是所求曲线方程为y=x+2. 北京邮电大学出版社
3 两边积分,得 y = 4x dx 3 即 其中C 是任意常数. 解 根据导数的几何意义,有 y = x + C 4 (6-2) 设曲线方程为 y y x = ( ), 例1 一曲线通过点(1, 3),且在该曲线上任一点P(x,y)处的 切线的斜率为 ,求这曲线的方程. 3 4x (6-1) d 3 ( ) 4 d y y x x x = = 于是所求曲线方程为 2. 4 y = x + 把 x=1,y=3代入(6-2)式,得 C =2 一、引例

第六章微分方程 高等数学少学时 例2一质量为的物体只受重力作用而自由下落,试确定该 物体下落的距离s与时间t的函数关系. 解设物体经过时刻t的位置为s=s(),物体受重力F=g d"s 的作用而自由下落,物体下落的加速度a= 由牛顿第二定律F=M,于是得物体在下落过程中,路程 S与时间t满足的关系式为 d2s d's dt2 =mg, 或d2 =S"(t)=g (6-3) 北京邮电大学出版社
4 例2 一质量为m的物体只受重力作用而自由下落,试确定该 物体下落的距离s 与时间 t 的函数关系. 解 设物体经过时刻 t 的位置为 s = s (t),物体受重力 F = mg 的作用而自由下落,物体下落的加速度 . d d 2 2 t s a = 由牛顿第二定律 F = ma, 于是得物体在下落过程中,路程 s 与时间 t 满足的关系式为 , d d 2 2 mg t s m = 或 2 2 d ( ) d s s t g t = = (6-3)

第六章微分方程 高等数学少学时 此外,未知函数s=S()还应满足下列条件: t=0时,S=0,y=45=0. ds (6-4) dt 把(6-3)式两端积分一次,得 ds V= =s'()=gt+C1, dt 再积分一次,得 s=28+Ct+C2, 1 其中C1,C2都是任意常数. 把条件t=0时,v=0代入(6-5)式,解得C1=0. 再把条件t=0时,s=0代入(6-6)式,解得C2=0. 1 物体下落的运动方程为5=28, 北京邮电大学出版社 5
5 此外,未知函数 s = s (t) 还应满足下列条件: 0. d d = 0 = 0, = = t s t 时,s v (6-4) 把(6-3)式两端积分一次,得 d ( ) d s v s t t = = = gt +C1 , (6-5) 再积分一次,得 , 2 1 1 2 2 s = gt +C t +C (6-6) 其中 1 2 C ,C 都是任意常数. 0. 把条件 t =0时, v =0代入(6-5)式,解得 C1 = 再把条件 t =0时, s =0代入(6-6)式,解得 0. C2 = 物体下落的运动方程为 . 2 1 2 s = gt
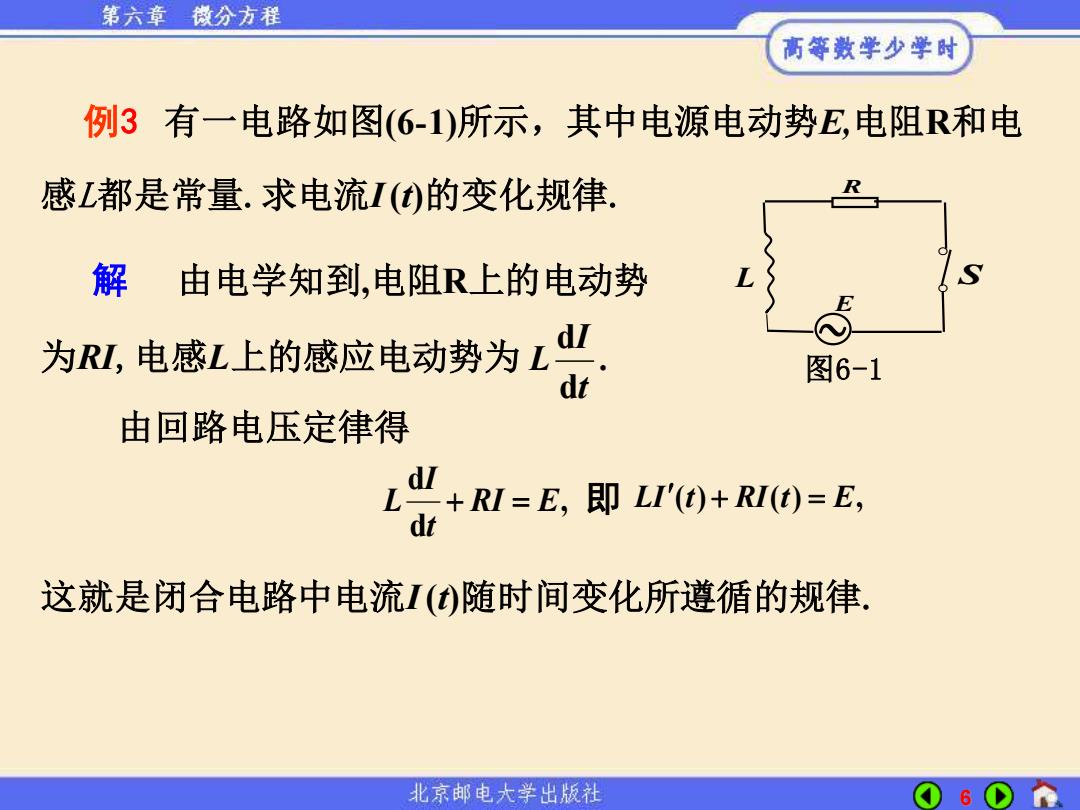
第六章微分方程 高等数学少学时 例3有一电路如图(6-1)所示,其中电源电动势E,电阻R和电 感L都是常量.求电流I()的变化规律 解由电学知到,电阻R上的电动势 d 为RL,电感L上的感应电动势为L dt 图6-1 由回路电压定律得 Ld业+RI=E,即LIr')+RI(0=E, dt 这就是闭合电路中电流I()随时间变化所遵循的规律。 北京邮电大学出版社 6
6 感L都是常量.求电流I (t)的变化规律. 解 由电学知到,电阻R上的电动势 . d d t I 为RI,电感L上的感应电动势为 L 由回路电压定律得 , d d RI E t I L + = 这就是闭合电路中电流I (t)随时间变化所遵循的规律. E ~ R 图6-1 L S 例3 有一电路如图(6-1)所示,其中电源电动势E,电阻R和电 即 LI t RI t E ( ) ( ) , + =

第六章 微分方程 高等数学少学时 微分方程: 含有未知函数导数(微分)的方程. 常微分方程:未知函数是一元函数的微分方程. 偏微分方程:未知函数是多元函数的微分方程 微分方程的阶:微分方程中所出现的未知函数的最高阶导数的阶数 例如: x2y+y2cosx-y'+ey"=0三阶微分方程. x4-c0s灯y俐=0 四阶微分方程 北京邮电大学出版社 7
7 微分方程: 含有未知函数导数(微分)的方程. 未知函数是一元函数的微分方程. 未知函数是多元函数的微分方程 . 微分方程的阶: cos 0 2 2 x y + y x − xy + e y = x 三阶微分方程. 常微分方程: 偏微分方程: 微分方程中所出现的未知函数的最高阶导数的阶数. 例如: ( ) cos 0 4 4 x − xy = 四阶微分方程

第六章微分方程 高等数学少学时 一般地,n阶微分方程的形式: F(,y,y,y”,,y)=0 注n阶微分方程中必须含有y,其余的变量可以不出现, 如y四+1=0; -2=0;5y"+y=7. dx 如果函数y=p(心)代入微分方程后,能使方程变为恒等式, 则称y=p(x为微分方程的解. 北京邮电大学出版社 8
8 ( ) ( , , , , , ) = 0 n F x y y y y 一般地,n阶微分方程的形式: 如 ( ) + 1 = 0; n y 2 0; d d d d 4 4 + − = x y x y 5 y + y = 7. 注 ( ) , n n 阶微分方程中必须含有 y 其余的变量可以不出现. 如果函数 y =(x) 代入微分方程后,能使方程变为恒等式, 则称 y =(x) 为微分方程的解

第六章微分方程 高等数学少学时 通解:解中独立的任意常数的个数等于微分方程的阶数的解 如: y=C1x+C2e*中的CC,是独立的, y=(C1+4C2)e*中的CC2是不独立的. 初始条件:问题中用于确定通解中的任意常数的条件, 特解: 利用初始条件确定出通解中的任意常数后得到的解 初值问题:求微分方程满足初始条件的特解的问题, 北京邮电大学出版社
9 通解: 解中独立的任意常数的个数等于微分方程的阶数的解. 如: x y C x C e = 1 + 2 中的 C1 、C2 是独立的, ( ) x y C C e = 1 + 4 2 中的 C1 、C2 是不独立的. 特解: 利用初始条件确定出通解中的任意常数后得到的解. 初始条件:问题中用于确定通解中的任意常数的条件. 初值问题:求微分方程满足初始条件的特解的问题

第六章微分方程 高等数学少学时 一般初值问题可写为 「F(k,y,y',y",…,y)=0 J。=0,y叫=,,y-叫=y- 微分方程的特解的图形是一条曲线,称为微分方程的积分曲线 微分方程的通解的图形是一族曲线,称为积分曲线族. 北京邮电大学出版社 10C
10 一般初值问题可写为 ( ) ( 1) 0 1 0 0 0 0 0 , ' , , − = − = = = = = n x x n x x x x y y y y y y ( ) ( , , ' , " , , )= 0 n F x y y y y 微分方程的特解的图形是一条曲线,称为微分方程的积分曲线. 微分方程的通解的图形是一族曲线,称为积分曲线族