
第五章 定积分 高等数学少学时 直角坐标 s=∫[f(x)-g(x]de s=[p(y)-w(y)]4 复习 一、 面积 参数方程S=∫yde=∫y()p'(t)dt 极坐标系 s=[p(o)]d6 平行截面面积已知的立体V=S(x)dr 二、体积 旋转体 .=∫[fx]'d ',=∫[p(]'d 直角坐标s=∫1+d 三、弧长 参数方程 s=∫Vp2()+y2(t)d 北京邮电大学出版社
1 b x a V f x x 2 = ( ) d b a V S x x = ( )d 二、体积 平行截面面积已知的立体 旋转体 2 π ( ) d d y c V y y = 2 1 ' d b a s y x = + 2 2 s t t t = + ' ( ) ' ( )d 三、弧长 直角坐标 参数方程 b a S f x g x x = − ( ) ( ) d ( ) 1 2 d 2 S = 一、面积 极坐标系 直角坐标 参数方程 b a S y x t t t = = d ( ) ( )d ( ) ( ) d c S y y y = − d 复习

第五章定积分 高等数学少学时 第六节定积分在物理学中的定用 一、变力沿直线所做的功 二、水压力 三、其他应用 北京邮电大学出版社
2 第六节 定积分在物理学中的应用 一、变力沿直线所做的功 三、其他应用 二、水压力

第五章 定积分 高等数学少学时 一、变力沿直线所做的功 F(x) 恒力作功:W=F·S xx+dx b x 设有一变力Fx)随位移x而变, 求它把物体由a移动到b所作的功. 取x为积分变量,它的变化区间为,b]在此区间上任取 小区间[,x+dx,在此小区间上变力所作的功近似等于以x点的 力为恒力所作的功,这个小区间功的近似值即为功元素,即 功元素为: dW=F(x)dx 于是所作的功为 W=∫F(x)d 北京邮电大学出版社 3
3 W = F s 取 x为积分变量,它的变化区间为[a, b],在此区间上任取 小区间[x, x+dx], 力为恒力所作的功, 在此小区间上变力所作的功近似等于以x点的 d ( )d W F x x = ( )d b a W F x x = • • x x+dx • • • O a b x F(x) 一、变力沿直线所做的功 恒力作功: 这个小区间功的近似值即为功元素,即 功元素为: 于是所作的功为 求它把物体由a 移动到 b 所作的功. 设有一变力F(x)随位移x而变
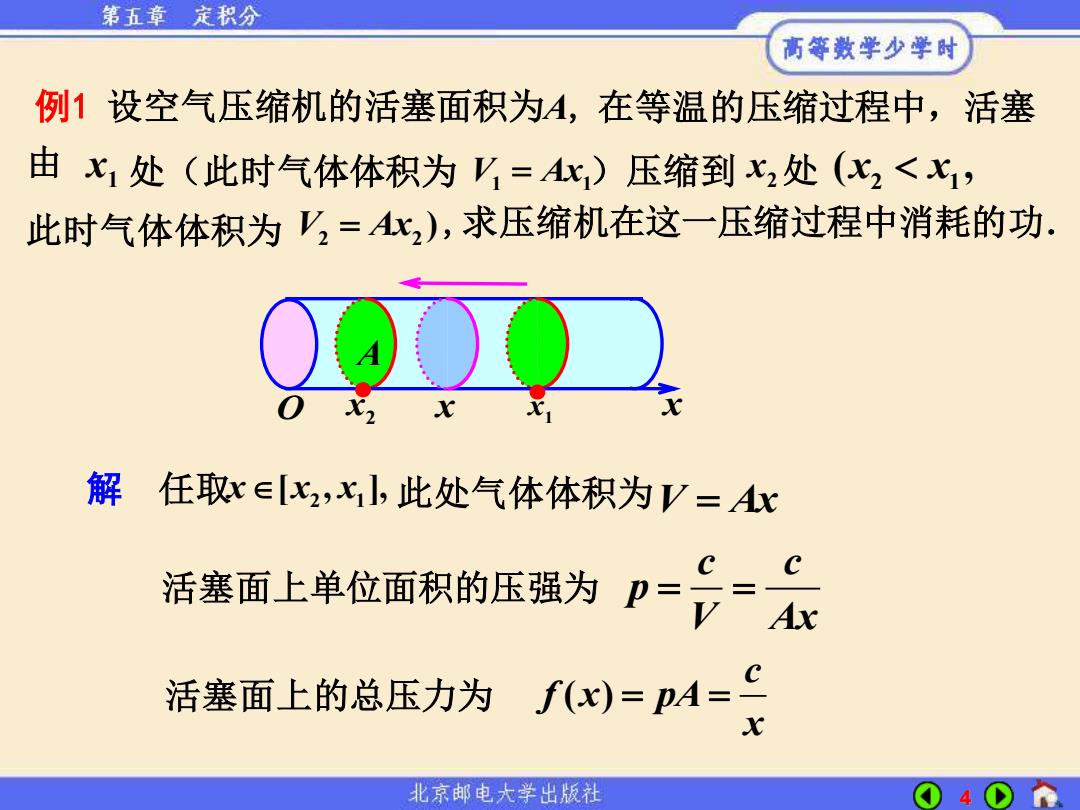
第五章 定积分 高等数学少学时 例1设空气压缩机的活塞面积为A,在等温的压缩过程中,活塞 由x1处(此时气体体积为V=Ax)压缩到x2处(x2<x1, 此时气体体积为V,=A比,),求压缩机在这一压缩过程中消耗的功. 解 任取x∈[x2,x,此处气体体积为V=Ax C 活塞面上单位面积的压强为 p= Ax 活塞面上的总压力为 f(x)=pA=c x 北京邮电大学出版社
4 V Ax = c c p V Ax = = c f x pA x ( ) = = 2 1 解 任取 x x x [ , ], 此处气体体积为 活塞面上单位面积的压强为 活塞面上的总压力为 此时气体体积为 x1 V Ax 1 1 = x2 V Ax 2 2 = ) 例1 设空气压缩机的活塞面积为A, 在等温的压缩过程中,活塞 处(此时气体体积为 )压缩到 处 ,求压缩机在这一压缩过程中消耗的功. x x 2 1 ( , x2 x O 1 x • • A x 由

第五章 定积分 高等数学少学时 于是在点x处压缩机消耗的功元素为 dw-Cdx c 压缩过程中所消耗的功为 w-aw-fsa-em x X2 北京邮电大学出版社 05C
5 d d c W x x = 1 1 2 2 1 2 d d ln x x x x c x W W x c x x = = = 于是在点x处压缩机消耗的功元素为 压缩过程中所消耗的功为

第五章 定积分 高等数学少学时 例2从地面垂直向上发射质量为m的火箭,当火箭距地面为 r时,求火箭克服地球引力所作的功. 解设地球半径为R,地球的质量为M,火箭距离地面的高度 为x,已知火箭的质量为m 由万有引力定律,火箭受到地球的引力为 Mm f(x)= (R+(其中为引力常数) 已知当x=0时,f=mg,即k Mm R mg ..k= Rg M .f= R'g Mm R'mg M (R+x) 2 (R+x)2 北京邮电大学出版社 6
6 R g k M 2 = R g Mm R mg f M R x R x 2 2 2 2 ( ) ( ) = = + + 例2 从地面垂直向上发射质量为m 的火箭,当火箭距地面为 解 设地球半径为R,地球的质量为M ,火箭距离地面的高度 为x ,已知火箭的质量为m. 由万有引力定律,火箭受到地球的引力为 2 ( ) ( ) Mm f x k R x = + (其中k为引力常数) 已知当 x = 0 时, f mg = Mm k mg R 2 ,即 = r 时,求火箭克服地球引力所作的功.

第五章 定积分 高等数学少学时 于是,在点x处,火箭克服地球引力所作的功元素为 dW=fdx= R'mg dx (R+x)2 从而,当火箭距离地面为r时,火箭克服地球引力所作的功为 w-fw R'mg Ri) 北京邮电大学出版社 )7
7 R mg W f x x R x 2 2 d d d ( ) = = + r r R mg W W x R x 2 2 0 0 d d ( ) = = + 于是,在点x 处,火箭克服地球引力所作的功元素为 从而,当火箭距离地面为r 时,火箭克服地球引力所作的功为 R mg R R r 2 1 1 = − +

第五章 定积分 高等数学少学时 例3*一圆柱形的贮水桶高为5m,底面半径为3m,桶内盛 满了水,试问要把桶内的水全部吸出需作多少功? 解把重量为G的物体提高高度为h需作的功是:W=Gh 建立如图所示的坐标系. 取深度x为积分变量,变化区间为0,5], 相应于[0,5]上任一小区间[x,x+dx] 的一薄层水被吸出需作的功的近似值 x+dx (即功元素)为dW=yV.x=Y·π(3)dxx (水的比重y=9.8kN/m) 北京邮电大学出版社
8 例3* 一圆柱形的贮水桶高为5 m,底面半径为3 m,桶内盛 满了水,试问要把桶内的水全部吸出需作多少功? 解 把重量为G 的物体提高高度为h需作的功是: W = Gh O x x+dx • • (即功元素)为 [ , d ] x x x + 2 dW V x x x = = π(3 )d 3 (水的比重 = 9.8kN/m) 相应于[0,5]上任一小区间 的一薄层水 建立如图所示的坐标系. 取深度 x为积分变量,变化区间为[0,5], 被吸出需作的功的近似值

第五章 定积分 高等数学少学时 于是所求的功为: W=88.2元rdr=88.2r 25 =88.2元· ≈3462(kJ) 2 北京邮电大学出版社
9 于是所求的功为: x W x x 2 5 0 5 88.2 d 88.2 2 0 = = 25 88.2 3462(kJ) 2 =
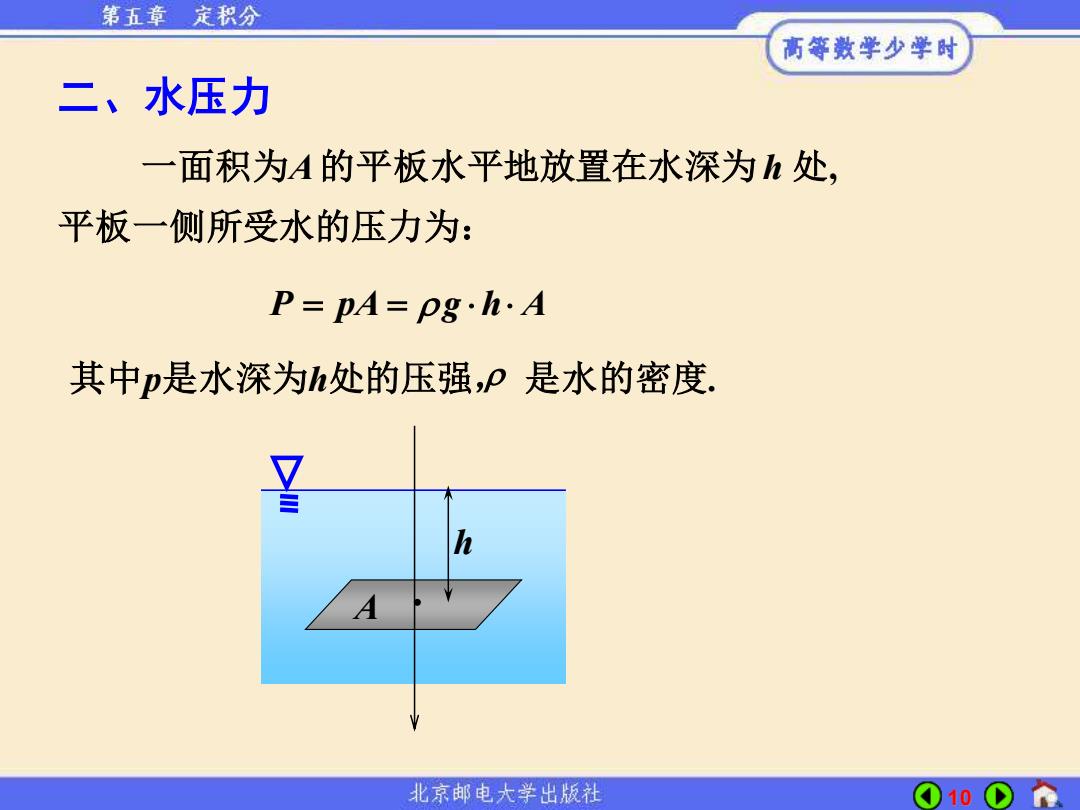
第五章定积分 高等数学少学时 二、水压力 一面积为A的平板水平地放置在水深为处, 平板一侧所受水的压力为: P=pA=pg·hA 其中p是水深为h处的压强,P是水的密度. 北京邮电大学出版社 10
10 二、水压力 · h A 一面积为A的平板水平地放置在水深为h 处, 平板一侧所受水的压力为: P pA g h A = = 其中p是水深为h处的压强, 是水的密度